Question-178626

Question Number 178626 by mr W last updated on 19/Oct/22

Commented by Frix last updated on 20/Oct/22

am I right with this conception? put 1 student of each college at a board and then “draw” the others which is the same as try each possible combination of the 10 remaining. we have 10! different combinations and if in a certain combination at least one pair of “friends” appears, this combination is not allowed

$$\mathrm{am}\:\mathrm{I}\:\mathrm{right}\:\mathrm{with}\:\mathrm{this}\:\mathrm{conception}? \\ $$$$\mathrm{put}\:\mathrm{1}\:\mathrm{student}\:\mathrm{of}\:\mathrm{each}\:\mathrm{college}\:\mathrm{at}\:\mathrm{a}\:\mathrm{board}\:\mathrm{and} \\ $$$$\mathrm{then}\:“\mathrm{draw}''\:\mathrm{the}\:\mathrm{others}\:\mathrm{which}\:\mathrm{is}\:\mathrm{the}\:\mathrm{same} \\ $$$$\mathrm{as}\:\mathrm{try}\:\mathrm{each}\:\mathrm{possible}\:\mathrm{combination}\:\mathrm{of}\:\mathrm{the}\:\mathrm{10} \\ $$$$\mathrm{remaining}.\:\mathrm{we}\:\mathrm{have}\:\mathrm{10}!\:\mathrm{different}\:\mathrm{combinations} \\ $$$$\mathrm{and}\:\mathrm{if}\:\mathrm{in}\:\mathrm{a}\:\mathrm{certain}\:\mathrm{combination}\:\mathrm{at}\:\mathrm{least}\:\mathrm{one} \\ $$$$\mathrm{pair}\:\mathrm{of}\:“\mathrm{friends}''\:\mathrm{appears},\:\mathrm{this}\:\mathrm{combination} \\ $$$$\mathrm{is}\:\mathrm{not}\:\mathrm{allowed} \\ $$

Commented by Frix last updated on 20/Oct/22

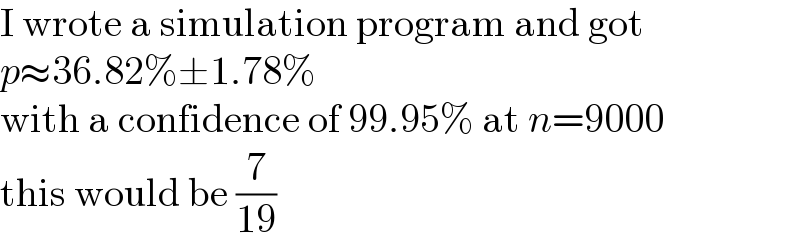
I wrote a simulation program and got p≈36.82%±1.78% with a confidence of 99.95% at n=9000 this would be (7/(19))

$$\mathrm{I}\:\mathrm{wrote}\:\mathrm{a}\:\mathrm{simulation}\:\mathrm{program}\:\mathrm{and}\:\mathrm{got} \\ $$$${p}\approx\mathrm{36}.\mathrm{82\%}\pm\mathrm{1}.\mathrm{78\%} \\ $$$$\mathrm{with}\:\mathrm{a}\:\mathrm{confidence}\:\mathrm{of}\:\mathrm{99}.\mathrm{95\%}\:\mathrm{at}\:{n}=\mathrm{9000} \\ $$$$\mathrm{this}\:\mathrm{would}\:\mathrm{be}\:\frac{\mathrm{7}}{\mathrm{19}} \\ $$

Commented by MJS_new last updated on 24/Oct/22

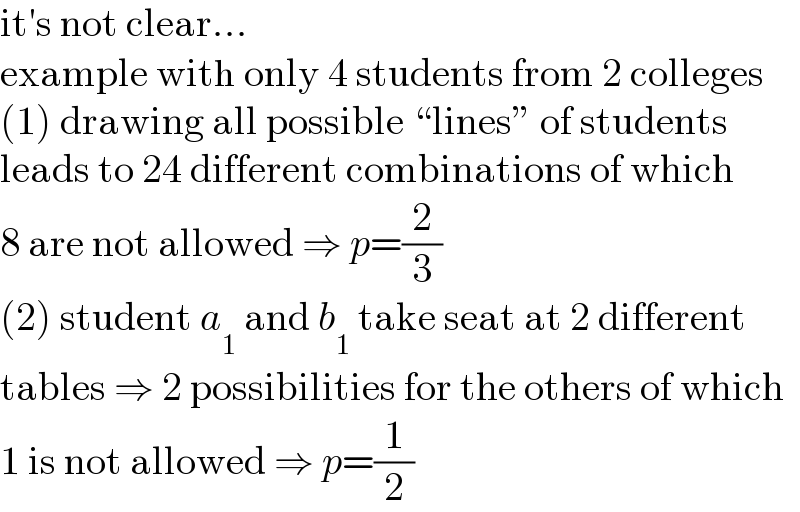
it′s not clear... example with only 4 students from 2 colleges (1) drawing all possible “lines” of students leads to 24 different combinations of which 8 are not allowed ⇒ p=(2/3) (2) student a_1 and b_1 take seat at 2 different tables ⇒ 2 possibilities for the others of which 1 is not allowed ⇒ p=(1/2)

$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{clear}… \\ $$$$\mathrm{example}\:\mathrm{with}\:\mathrm{only}\:\mathrm{4}\:\mathrm{students}\:\mathrm{from}\:\mathrm{2}\:\mathrm{colleges} \\ $$$$\left(\mathrm{1}\right)\:\mathrm{drawing}\:\mathrm{all}\:\mathrm{possible}\:“\mathrm{lines}''\:\mathrm{of}\:\mathrm{students} \\ $$$$\mathrm{leads}\:\mathrm{to}\:\mathrm{24}\:\mathrm{different}\:\mathrm{combinations}\:\mathrm{of}\:\mathrm{which} \\ $$$$\mathrm{8}\:\mathrm{are}\:\mathrm{not}\:\mathrm{allowed}\:\Rightarrow\:{p}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\left(\mathrm{2}\right)\:\mathrm{student}\:{a}_{\mathrm{1}} \:\mathrm{and}\:{b}_{\mathrm{1}} \:\mathrm{take}\:\mathrm{seat}\:\mathrm{at}\:\mathrm{2}\:\mathrm{different} \\ $$$$\mathrm{tables}\:\Rightarrow\:\mathrm{2}\:\mathrm{possibilities}\:\mathrm{for}\:\mathrm{the}\:\mathrm{others}\:\mathrm{of}\:\mathrm{which} \\ $$$$\mathrm{1}\:\mathrm{is}\:\mathrm{not}\:\mathrm{allowed}\:\Rightarrow\:{p}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Answered by Acem last updated on 19/Oct/22

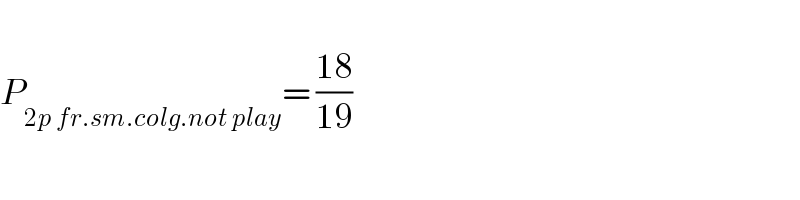
P_(2p fr.sm.colg.not play) = ((18)/(19))

$$ \\ $$$${P}_{\mathrm{2}{p}\:{fr}.{sm}.{colg}.{not}\:{play}} =\:\frac{\mathrm{18}}{\mathrm{19}} \\ $$

Commented by Acem last updated on 19/Oct/22

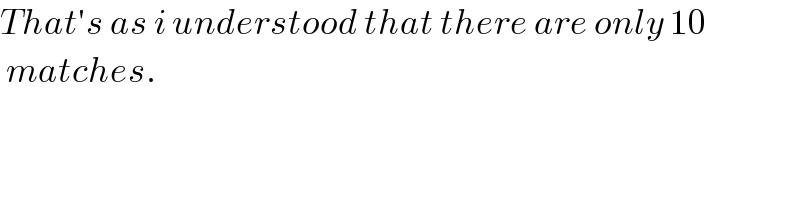
That′s as i understood that there are only 10 matches.

$${That}'{s}\:{as}\:{i}\:{understood}\:{that}\:{there}\:{are}\:{only}\:\mathrm{10} \\ $$$$\:{matches}. \\ $$

Commented by Frix last updated on 19/Oct/22

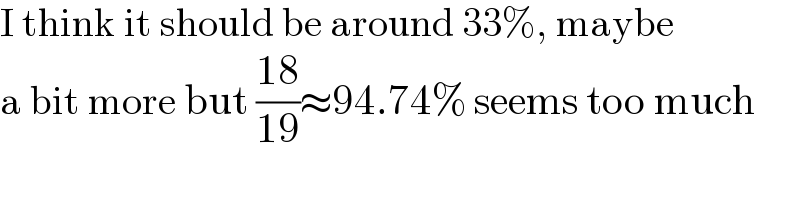
I think it should be around 33%, maybe a bit more but ((18)/(19))≈94.74% seems too much

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\mathrm{around}\:\mathrm{33\%},\:\mathrm{maybe} \\ $$$$\mathrm{a}\:\mathrm{bit}\:\mathrm{more}\:\mathrm{but}\:\frac{\mathrm{18}}{\mathrm{19}}\approx\mathrm{94}.\mathrm{74\%}\:\mathrm{seems}\:\mathrm{too}\:\mathrm{much} \\ $$

Commented by Acem last updated on 19/Oct/22

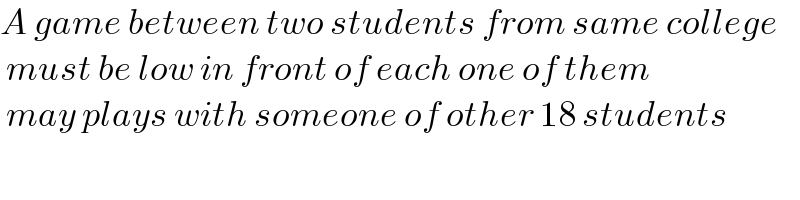
A game between two students from same college must be low in front of each one of them may plays with someone of other 18 students

$${A}\:{game}\:{between}\:{two}\:{students}\:{from}\:{same}\:{college} \\ $$$$\:{must}\:{be}\:{low}\:{in}\:{front}\:{of}\:{each}\:{one}\:{of}\:{them} \\ $$$$\:{may}\:{plays}\:{with}\:{someone}\:{of}\:{other}\:\mathrm{18}\:{students} \\ $$

Commented by mr W last updated on 19/Oct/22

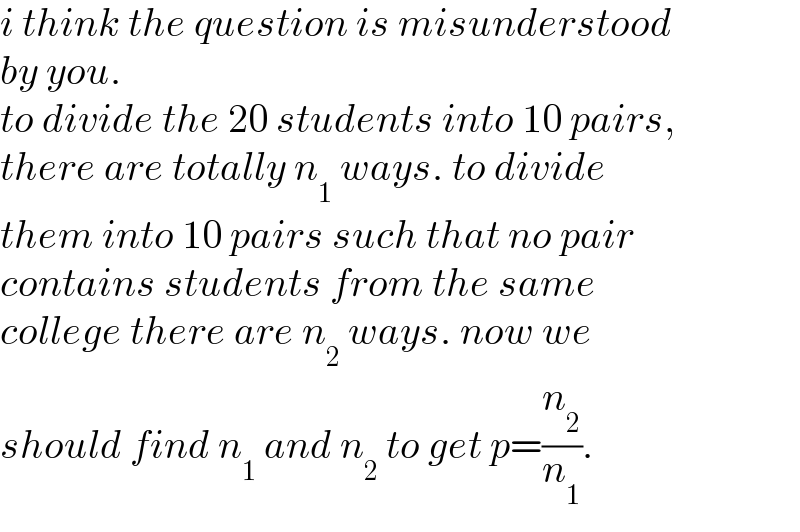
i think the question is misunderstood by you. to divide the 20 students into 10 pairs, there are totally n_1 ways. to divide them into 10 pairs such that no pair contains students from the same college there are n_2 ways. now we should find n_1 and n_2 to get p=(n_2 /n_1 ).

$${i}\:{think}\:{the}\:{question}\:{is}\:{misunderstood} \\ $$$${by}\:{you}. \\ $$$${to}\:{divide}\:{the}\:\mathrm{20}\:{students}\:{into}\:\mathrm{10}\:{pairs}, \\ $$$${there}\:{are}\:{totally}\:{n}_{\mathrm{1}} \:{ways}.\:{to}\:{divide} \\ $$$${them}\:{into}\:\mathrm{10}\:{pairs}\:{such}\:{that}\:{no}\:{pair}\: \\ $$$${contains}\:{students}\:{from}\:{the}\:{same} \\ $$$${college}\:{there}\:{are}\:{n}_{\mathrm{2}} \:{ways}.\:{now}\:{we} \\ $$$${should}\:{find}\:{n}_{\mathrm{1}} \:{and}\:{n}_{\mathrm{2}} \:{to}\:{get}\:{p}=\frac{{n}_{\mathrm{2}} }{{n}_{\mathrm{1}} }. \\ $$

Commented by Acem last updated on 20/Oct/22

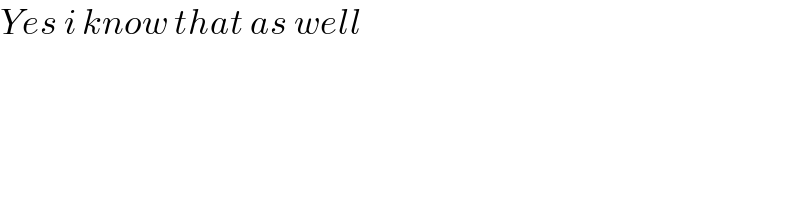
$${Yes}\:{i}\:{know}\:{that}\:{as}\:{well} \\ $$

Commented by mr W last updated on 20/Oct/22

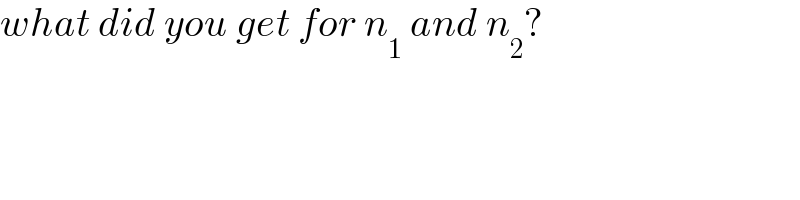
$${what}\:{did}\:{you}\:{get}\:{for}\:{n}_{\mathrm{1}} \:{and}\:{n}_{\mathrm{2}} ? \\ $$

Commented by Acem last updated on 20/Oct/22

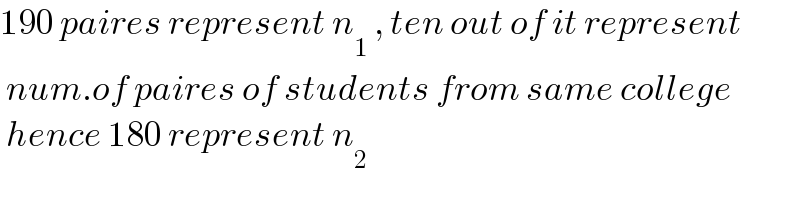
190 paires represent n_1 , ten out of it represent num.of paires of students from same college hence 180 represent n_2

$$\mathrm{190}\:{paires}\:{represent}\:{n}_{\mathrm{1}} \:,\:{ten}\:{out}\:{of}\:{it}\:{represent} \\ $$$$\:{num}.{of}\:{paires}\:{of}\:{students}\:{from}\:{same}\:{college} \\ $$$$\:{hence}\:\mathrm{180}\:{represent}\:{n}_{\mathrm{2}} \\ $$

Commented by mr W last updated on 20/Oct/22

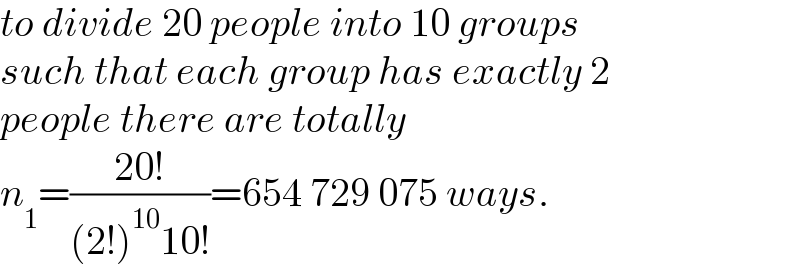
to divide 20 people into 10 groups such that each group has exactly 2 people there are totally n_1 =((20!)/((2!)^(10) 10!))=654 729 075 ways.

$${to}\:{divide}\:\mathrm{20}\:{people}\:{into}\:\mathrm{10}\:{groups} \\ $$$${such}\:{that}\:{each}\:{group}\:{has}\:{exactly}\:\mathrm{2} \\ $$$${people}\:{there}\:{are}\:{totally} \\ $$$${n}_{\mathrm{1}} =\frac{\mathrm{20}!}{\left(\mathrm{2}!\right)^{\mathrm{10}} \mathrm{10}!}=\mathrm{654}\:\mathrm{729}\:\mathrm{075}\:{ways}. \\ $$

Commented by Acem last updated on 20/Oct/22

$${You}\:{are}\:{correct}\:{about}\:{this},\:{but}\:{what}'{s}\:{the}\:{point} \\ $$$$\:{of}\:{dividing}\:{them}\:{into}\:{these}\:{groups}\:{by}\:{this}\:{method} \\ $$$$\:{as}\:{long}\:{as}\:{every}\:{student}\:{may}\:{plays}\:{against}\:{only} \\ $$$$\:{one}\:{of}\:\mathrm{19}\:{other}\:{opponents}\:{with}\:{exception}\:{of} \\ $$$$\:{repetition}.\:{At}\:{that}\:{time}\:{we}\:{get}\:\:\mathrm{190}\:{possible} \\ $$$$\:{paires}\:{as}\:{a}\:{sample}\:{space}. \\ $$$$ \\ $$

Commented by Acem last updated on 20/Oct/22

Give me a sample of some elements of the sample space other the {(Jack_(col.1) , Toni_(col.8) ), (Jack_(col1) , Smith_(col.3) ).... (Sam_(col.1) , Jeorge_(col.5) )..., (Jack_(col.1) , Sam_(col.1) ).....} and number of these pairses are 190

$${Give}\:{me}\:{a}\:{sample}\:{of}\:{some}\:{elements}\:{of}\:{the}\: \\ $$$$\:{sample}\:{space}\:{other}\:{the}\:\left\{\left({Jack}_{{col}.\mathrm{1}} ,\:{Toni}_{{col}.\mathrm{8}} \right),\right. \\ $$$$\:\left({Jack}_{{col}\mathrm{1}} ,\:{Smith}_{{col}.\mathrm{3}} \right)….\:\left({Sam}_{{col}.\mathrm{1}} ,\:{Jeorge}_{{col}.\mathrm{5}} \right)…, \\ $$$$\left.\:\left({Jack}_{{col}.\mathrm{1}} ,\:{Sam}_{{col}.\mathrm{1}} \right)…..\right\} \\ $$$$\:{and}\:{number}\:{of}\:{these}\:{pairses}\:{are}\:\mathrm{190} \\ $$$$ \\ $$

Commented by mr W last updated on 20/Oct/22

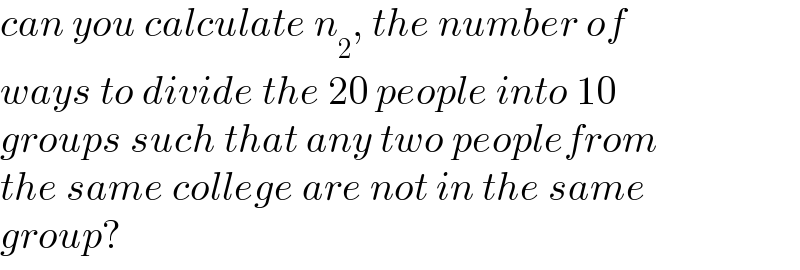
can you calculate n_2 , the number of ways to divide the 20 people into 10 groups such that any two peoplefrom the same college are not in the same group?

$${can}\:{you}\:{calculate}\:{n}_{\mathrm{2}} ,\:{the}\:{number}\:{of} \\ $$$${ways}\:{to}\:{divide}\:{the}\:\mathrm{20}\:{people}\:{into}\:\mathrm{10} \\ $$$${groups}\:{such}\:{that}\:{any}\:{two}\:{peoplefrom} \\ $$$${the}\:{same}\:{college}\:{are}\:{not}\:{in}\:{the}\:{same} \\ $$$${group}? \\ $$

Commented by Acem last updated on 21/Oct/22

Forming paires: 10_(10 Col.) ^(ways) ×2∣×9_(9 col.) ^(w.) ×2 ⇒ 1st_P (Jack, Toni) 2_(2Col.) ^(ways) ×1∣×1_(1 col.) ^(w.) +^(OR) 2_(2Col.) ^(ways) ×1∣×9_(1 col.) ^(w.) ×1 +^(OR) 8_(frm 8 Col.) ^(ways) ×2∣×7_(frm 7 col.) ^(w.) ×2 ⇒ 2nd_P (Sam, Dani) 2_(frm 2Col.) ^(ways) ×1∣×1_(frm 1 col.) ^(w.) +^(OR) complex ways +^(OR) 6_(frm 6 Col.) ^(ways) ×2∣×5_(frm 5 col.) ^(w.) ×2 ⇒ 3rd_P (You, Me) ⋮ ⋮ The tenth pairse: 2_(2Col.) ^(here i think 1 way not 2) ×1∣_(9th Col.) ×1_(1 col.) ^(w.) ∣_(10th Col) ⇒ 10th_P (Tom, Paskal) n_2 = Sum above That′s a high hard work, and i don′t know why Hey students shake hands with each other! And i get 190 paires belong to the Sample Space Ten out of it represent 2stu.frm.sm.Col.

$${Forming}\:{paires}: \\ $$$$\:\mathrm{10}_{\mathrm{10}\:{Col}.} ^{{ways}} ×\mathrm{2}\mid×\mathrm{9}_{\mathrm{9}\:{col}.} ^{{w}.} ×\mathrm{2}\:\:\Rightarrow\:\mathrm{1}{st}_{{P}} \:\left({Jack},\:{Toni}\right) \\ $$$$ \\ $$$$\:\mathrm{2}_{\mathrm{2}{Col}.} ^{{ways}} ×\mathrm{1}\mid×\mathrm{1}_{\mathrm{1}\:{col}.} ^{{w}.} \:\overset{{OR}} {+}\:\mathrm{2}_{\mathrm{2}{Col}.} ^{{ways}} ×\mathrm{1}\mid×\mathrm{9}_{\mathrm{1}\:{col}.} ^{{w}.} ×\mathrm{1}\:\overset{{OR}} {+} \\ $$$$\:\mathrm{8}_{{frm}\:\mathrm{8}\:{Col}.} ^{{ways}} ×\mathrm{2}\mid×\mathrm{7}_{{frm}\:\mathrm{7}\:{col}.} ^{{w}.} ×\mathrm{2}\:\Rightarrow\:\mathrm{2}{nd}_{{P}} \:\left({Sam},\:{Dani}\right) \\ $$$$ \\ $$$$\:\mathrm{2}_{{frm}\:\mathrm{2}{Col}.} ^{{ways}} ×\mathrm{1}\mid×\mathrm{1}_{{frm}\:\mathrm{1}\:{col}.} ^{{w}.} \:\overset{{OR}} {+}\:{complex}\:{ways}\:\overset{{OR}} {+} \\ $$$$\:\mathrm{6}_{{frm}\:\mathrm{6}\:{Col}.} ^{{ways}} ×\mathrm{2}\mid×\mathrm{5}_{{frm}\:\mathrm{5}\:{col}.} ^{{w}.} ×\mathrm{2}\:\Rightarrow\:\mathrm{3}{rd}_{{P}} \:\left({You},\:{Me}\right) \\ $$$$\vdots \\ $$$$\vdots \\ $$$${The}\:{tenth}\:{pairse}: \\ $$$$\:\mathrm{2}_{\mathrm{2}{Col}.} ^{{here}\:{i}\:{think}\:\mathrm{1}\:{way}\:{not}\:\mathrm{2}} ×\mathrm{1}\mid_{\mathrm{9}{th}\:{Col}.} ×\mathrm{1}_{\mathrm{1}\:{col}.} ^{{w}.} \mid_{\mathrm{10}{th}\:{Col}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Rightarrow\:\mathrm{10}{th}_{{P}} \:\left({Tom},\:{Paskal}\right) \\ $$$$\:{n}_{\mathrm{2}} =\:{Sum}\:{above} \\ $$$$\: \\ $$$${That}'{s}\:{a}\:{high}\:{hard}\:{work},\:{and}\:{i}\:{don}'{t}\:{know}\:{why} \\ $$$$ \\ $$$$\boldsymbol{{Hey}}\:\boldsymbol{{students}}\:{shake}\:{hands}\:{with}\:{each}\:{other}! \\ $$$$ \\ $$$${And}\:{i}\:{get}\:\mathrm{190}\:{paires}\:{belong}\:{to}\:{the}\:\boldsymbol{{Sample}}\:\boldsymbol{{Space}} \\ $$$$ \\ $$$$\:{Ten}\:{out}\:{of}\:{it}\:{represent}\:\mathrm{2}{stu}.{frm}.{sm}.{Col}. \\ $$$$ \\ $$$$ \\ $$

Commented by Acem last updated on 21/Oct/22

Can you give me a sample of some elements of the sample space other the {(Jack_(col.1) , Toni_(col.8) ), (Jack_(col1) , Smith_(col.3) ).... (Sam_(col.1) , Jeorge_(col.5) )..., (Jack_(col.1) , Sam_(col.1) ).....} and number of these pairses are 190

$$ \\ $$$${Can}\:{you}\:{give}\:{me}\:{a}\:{sample}\:{of}\:{some}\:{elements} \\ $$$$\:{of}\:{the}\:\:{sample}\:{space}\:{other}\:{the}\:\left\{\left({Jack}_{{col}.\mathrm{1}} ,\:{Toni}_{{col}.\mathrm{8}} \right),\right. \\ $$$$\:\left({Jack}_{{col}\mathrm{1}} ,\:{Smith}_{{col}.\mathrm{3}} \right)….\:\left({Sam}_{{col}.\mathrm{1}} ,\:{Jeorge}_{{col}.\mathrm{5}} \right)…, \\ $$$$\left.\:\left({Jack}_{{col}.\mathrm{1}} ,\:{Sam}_{{col}.\mathrm{1}} \right)…..\right\} \\ $$$$\:{and}\:{number}\:{of}\:{these}\:{pairses}\:{are}\:\mathrm{190} \\ $$$$ \\ $$

Commented by Acem last updated on 21/Oct/22

This issue confused me. At first i thought just like you, then i turned my attention to interresting of that each one can′t play but with one of 19 person, therefore i formed the sample space above and it is true.... thought it′s true.... it′s not true! and the issue is not here, it′s about forming 10 mathces, so the sample space is for matches not for people. Each item of this sample space represent 10 games “10 pairses”. What i′ve just said i think it′s correcrt, but really this issue made me feel tired

$${This}\:{issue}\:{confused}\:{me}.\:{At}\:{first}\:{i}\:{thought}\:{just} \\ $$$$\:{like}\:{you},\:{then}\:{i}\:{turned}\:{my}\:{attention}\:{to}\:{interresting} \\ $$$$\:{of}\:\:{that}\:{each}\:{one}\:{can}'{t}\:{play}\:{but}\:{with}\:{one}\:{of}\:\mathrm{19}\:{person}, \\ $$$$\:{therefore}\:{i}\:{formed}\:{the}\:{sample}\:{space}\:{above}\:{and}\:{it} \\ $$$$\:{is}\:{true}….\:{thought}\:{it}'{s}\:{true}….\:{it}'{s}\:{not}\:{true}!\:{and} \\ $$$$\:{the}\:{issue}\:{is}\:{not}\:{here},\:{it}'{s}\:{about}\:{forming} \\ $$$$\:\mathrm{10}\:{mathces},\:{so}\:{the}\:{sample}\:{space}\:{is}\:{for}\:{matches} \\ $$$$\:{not}\:{for}\:{people}.\:{Each}\:{item}\:{of}\:{this}\:{sample} \\ $$$$\:{space}\:{represent}\:\mathrm{10}\:{games}\:“\mathrm{10}\:{pairses}''. \\ $$$$ \\ $$$$\:{What}\:{i}'{ve}\:{just}\:{said}\:{i}\:{think}\:{it}'{s}\:{correcrt},\:{but}\:{really} \\ $$$$\:{this}\:{issue}\:{made}\:{me}\:{feel}\:{tired} \\ $$

Commented by mr W last updated on 21/Oct/22

$${this}\:{is}\:{a}\:{very}\:{old}\:{question}\:{in}\:{the}\:{forum} \\ $$$${which}\:{is}\:{not}\:{solved}\:{yet}. \\ $$

Commented by mr W last updated on 21/Oct/22

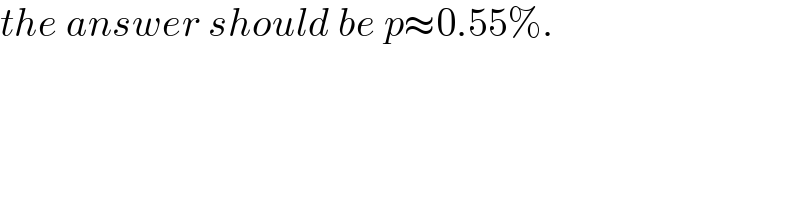
$${the}\:{answer}\:{should}\:{be}\:{p}\approx\mathrm{0}.\mathrm{55\%}. \\ $$

Commented by MJS_new last updated on 24/Oct/22

where is this answer from? I tried to figure how this develops. with n=4 players we have 12 34 × 13 24 ✓ 14 23 ✓ each stands for 2^(n/2) ×(n/2)!=8 combinations with n=6 players we have 12 34 56 × 12 35 46 × 12 36 45 × 13 24 56 × 13 25 46 ✓ 13 26 45 ✓ 14 23 56 × 14 25 36 ✓ 14 26 35 ✓ 15 23 46 ✓ 15 24 36 ✓ 15 26 34 × 16 23 45 ✓ 16 24 35 ✓ 16 25 34 × each stands for 2^(n/2) ×(n/2)!=48 combinations I also did this for n=8 it seems to me to follow this rule: n=4 N_4 =3 P_4 =1 p=(P_4 /N_4 )=(1/3) n=6 N_6 =5N_4 =15 P_6 =N_4 (1+(5−1)/3)=7 p=(P_6 /N_6 )=(7/(15)) n=8 N_8 =7N_6 =105 P_8 =N_6 (1+(7−1)/3)=45 p=(P_8 /N_8 )=((45)/(105))=(3/7) n=2k N_(2k) =(2k−1)N_(2k−2) P_(2k) =N_(2k−2) (1+(2k−1)/3) p=(P_(2k) /N_(2k) ) maybe somebody can verify this but for n=20 this gives (7/(19))

$$\mathrm{where}\:\mathrm{is}\:\mathrm{this}\:\mathrm{answer}\:\mathrm{from}? \\ $$$$\mathrm{I}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{figure}\:\mathrm{how}\:\mathrm{this}\:\mathrm{develops}. \\ $$$$\mathrm{with}\:{n}=\mathrm{4}\:\mathrm{players}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{12}\:\mathrm{34}\:× \\ $$$$\mathrm{13}\:\mathrm{24}\:\checkmark \\ $$$$\mathrm{14}\:\mathrm{23}\:\checkmark \\ $$$$\mathrm{each}\:\mathrm{stands}\:\mathrm{for}\:\mathrm{2}^{{n}/\mathrm{2}} ×\left({n}/\mathrm{2}\right)!=\mathrm{8}\:\mathrm{combinations} \\ $$$$\mathrm{with}\:{n}=\mathrm{6}\:\mathrm{players}\:\mathrm{we}\:\mathrm{have} \\ $$$$\mathrm{12}\:\mathrm{34}\:\mathrm{56}\:× \\ $$$$\mathrm{12}\:\mathrm{35}\:\mathrm{46}\:× \\ $$$$\mathrm{12}\:\mathrm{36}\:\mathrm{45}\:× \\ $$$$\mathrm{13}\:\mathrm{24}\:\mathrm{56}\:× \\ $$$$\mathrm{13}\:\mathrm{25}\:\mathrm{46}\:\checkmark \\ $$$$\mathrm{13}\:\mathrm{26}\:\mathrm{45}\:\checkmark \\ $$$$\mathrm{14}\:\mathrm{23}\:\mathrm{56}\:× \\ $$$$\mathrm{14}\:\mathrm{25}\:\mathrm{36}\:\checkmark \\ $$$$\mathrm{14}\:\mathrm{26}\:\mathrm{35}\:\checkmark \\ $$$$\mathrm{15}\:\mathrm{23}\:\mathrm{46}\:\checkmark \\ $$$$\mathrm{15}\:\mathrm{24}\:\mathrm{36}\:\checkmark \\ $$$$\mathrm{15}\:\mathrm{26}\:\mathrm{34}\:× \\ $$$$\mathrm{16}\:\mathrm{23}\:\mathrm{45}\:\checkmark \\ $$$$\mathrm{16}\:\mathrm{24}\:\mathrm{35}\:\checkmark \\ $$$$\mathrm{16}\:\mathrm{25}\:\mathrm{34}\:× \\ $$$$\mathrm{each}\:\mathrm{stands}\:\mathrm{for}\:\mathrm{2}^{{n}/\mathrm{2}} ×\left({n}/\mathrm{2}\right)!=\mathrm{48}\:\mathrm{combinations} \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{also}\:\mathrm{did}\:\mathrm{this}\:\mathrm{for}\:{n}=\mathrm{8} \\ $$$$\mathrm{it}\:\mathrm{seems}\:\mathrm{to}\:\mathrm{me}\:\mathrm{to}\:\mathrm{follow}\:\mathrm{this}\:\mathrm{rule}: \\ $$$${n}=\mathrm{4}\:{N}_{\mathrm{4}} =\mathrm{3}\:{P}_{\mathrm{4}} =\mathrm{1}\:{p}=\frac{{P}_{\mathrm{4}} }{{N}_{\mathrm{4}} }=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${n}=\mathrm{6}\:{N}_{\mathrm{6}} =\mathrm{5}{N}_{\mathrm{4}} =\mathrm{15}\:{P}_{\mathrm{6}} ={N}_{\mathrm{4}} \left(\mathrm{1}+\left(\mathrm{5}−\mathrm{1}\right)/\mathrm{3}\right)=\mathrm{7}\:{p}=\frac{{P}_{\mathrm{6}} }{{N}_{\mathrm{6}} }=\frac{\mathrm{7}}{\mathrm{15}} \\ $$$${n}=\mathrm{8}\:{N}_{\mathrm{8}} =\mathrm{7}{N}_{\mathrm{6}} =\mathrm{105}\:{P}_{\mathrm{8}} ={N}_{\mathrm{6}} \left(\mathrm{1}+\left(\mathrm{7}−\mathrm{1}\right)/\mathrm{3}\right)=\mathrm{45}\:{p}=\frac{{P}_{\mathrm{8}} }{{N}_{\mathrm{8}} }=\frac{\mathrm{45}}{\mathrm{105}}=\frac{\mathrm{3}}{\mathrm{7}} \\ $$$${n}=\mathrm{2}{k}\:{N}_{\mathrm{2}{k}} =\left(\mathrm{2}{k}−\mathrm{1}\right){N}_{\mathrm{2}{k}−\mathrm{2}} \:{P}_{\mathrm{2}{k}} ={N}_{\mathrm{2}{k}−\mathrm{2}} \left(\mathrm{1}+\left(\mathrm{2}{k}−\mathrm{1}\right)/\mathrm{3}\right)\:{p}=\frac{{P}_{\mathrm{2}{k}} }{{N}_{\mathrm{2}{k}} } \\ $$$$\mathrm{maybe}\:\mathrm{somebody}\:\mathrm{can}\:\mathrm{verify}\:\mathrm{this}\:\mathrm{but}\:\mathrm{for} \\ $$$${n}=\mathrm{20}\:\mathrm{this}\:\mathrm{gives}\:\frac{\mathrm{7}}{\mathrm{19}} \\ $$

Commented by Frix last updated on 24/Oct/22

but your p is the “wrong side”, you must take 1−p

$$\mathrm{but}\:\mathrm{your}\:{p}\:\mathrm{is}\:\mathrm{the}\:“\mathrm{wrong}\:\mathrm{side}'',\:\mathrm{you}\:\mathrm{must} \\ $$$$\mathrm{take}\:\mathrm{1}−{p} \\ $$

Commented by MJS_new last updated on 24/Oct/22

$$\mathrm{yes}\:\mathrm{you}'\mathrm{re}\:\mathrm{right} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply