Question Number 178647 by infinityaction last updated on 19/Oct/22
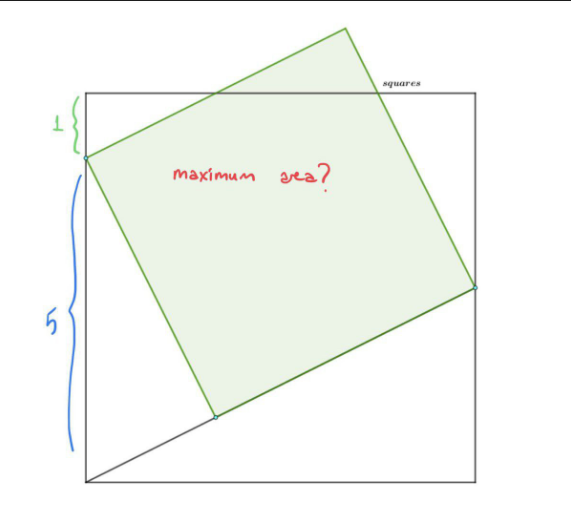
Answered by mr W last updated on 19/Oct/22
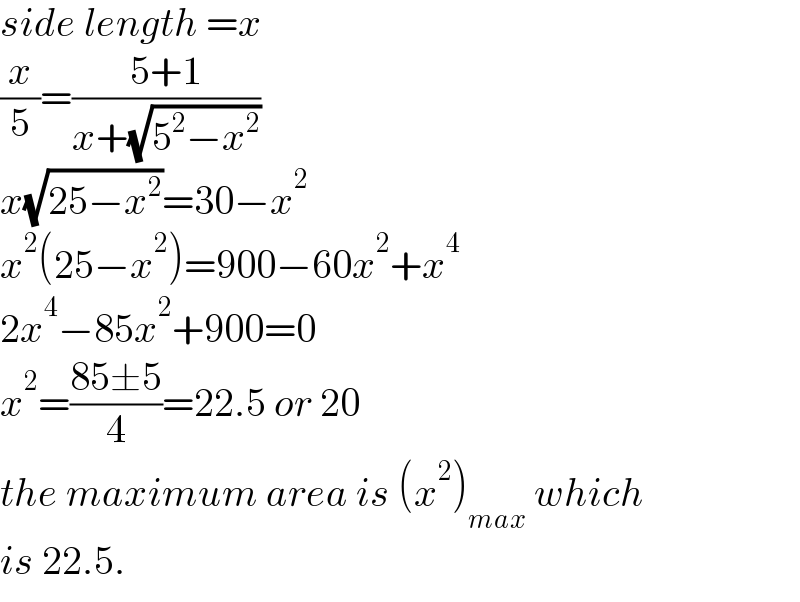
$${side}\:{length}\:={x} \\ $$$$\frac{{x}}{\mathrm{5}}=\frac{\mathrm{5}+\mathrm{1}}{{x}+\sqrt{\mathrm{5}^{\mathrm{2}} −{x}^{\mathrm{2}} }} \\ $$$${x}\sqrt{\mathrm{25}−{x}^{\mathrm{2}} }=\mathrm{30}−{x}^{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} \left(\mathrm{25}−{x}^{\mathrm{2}} \right)=\mathrm{900}−\mathrm{60}{x}^{\mathrm{2}} +{x}^{\mathrm{4}} \\ $$$$\mathrm{2}{x}^{\mathrm{4}} −\mathrm{85}{x}^{\mathrm{2}} +\mathrm{900}=\mathrm{0} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{85}\pm\mathrm{5}}{\mathrm{4}}=\mathrm{22}.\mathrm{5}\:{or}\:\mathrm{20} \\ $$$${the}\:{maximum}\:{area}\:{is}\:\left({x}^{\mathrm{2}} \right)_{{max}} \:{which} \\ $$$${is}\:\mathrm{22}.\mathrm{5}. \\ $$
Commented by infinityaction last updated on 20/Oct/22

$${thanks}\:{sir} \\ $$
Commented by Tawa11 last updated on 20/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
