Menu Close

Question-17869

Tinku Tara 0 Comments
Pin




Question Number 17869 by ajfour last updated on 11/Jul/17
Commented by ajfour last updated on 11/Jul/17
Q.17852 (solution)
$$\mathrm{Q}.\mathrm{17852}\:\:\left(\mathrm{solution}\right) \\ $$
Answered by ajfour last updated on 11/Jul/17
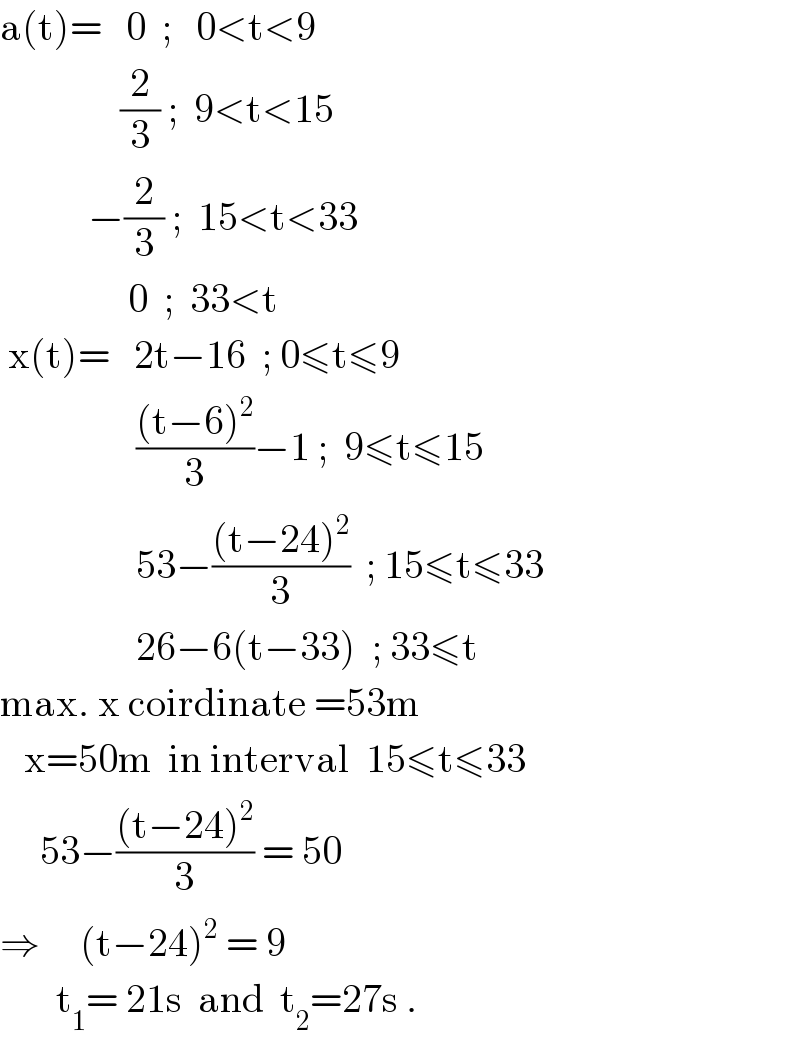
a(t)= 0 ; 0<t<9 (2/3) ; 9<t<15 −(2/3) ; 15<t<33 0 ; 33<t x(t)= 2t−16 ; 0≤t≤9 (((t−6)^2 )/3)−1 ; 9≤t≤15 53−(((t−24)^2 )/3) ; 15≤t≤33 26−6(t−33) ; 33≤t max. x coirdinate =53m x=50m in interval 15≤t≤33 53−(((t−24)^2 )/3) = 50 ⇒ (t−24)^2 = 9 t_1 = 21s and t_2 =27s .
$$\mathrm{a}\left(\mathrm{t}\right)=\:\:\:\mathrm{0}\:\:;\:\:\:\mathrm{0}<\mathrm{t}<\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\:;\:\:\mathrm{9}<\mathrm{t}<\mathrm{15} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\frac{\mathrm{2}}{\mathrm{3}}\:;\:\:\mathrm{15}<\mathrm{t}<\mathrm{33} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{0}\:\:;\:\:\mathrm{33}<\mathrm{t} \\ $$$$\:\mathrm{x}\left(\mathrm{t}\right)=\:\:\:\mathrm{2t}−\mathrm{16}\:\:;\:\mathrm{0}\leqslant\mathrm{t}\leqslant\mathrm{9}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\left(\mathrm{t}−\mathrm{6}\right)^{\mathrm{2}} }{\mathrm{3}}−\mathrm{1}\:;\:\:\mathrm{9}\leqslant\mathrm{t}\leqslant\mathrm{15} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{53}−\frac{\left(\mathrm{t}−\mathrm{24}\right)^{\mathrm{2}} }{\mathrm{3}}\:\:;\:\mathrm{15}\leqslant\mathrm{t}\leqslant\mathrm{33} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{26}−\mathrm{6}\left(\mathrm{t}−\mathrm{33}\right)\:\:;\:\mathrm{33}\leqslant\mathrm{t} \\ $$$$\mathrm{max}.\:\mathrm{x}\:\mathrm{coirdinate}\:=\mathrm{53m} \\ $$$$\:\:\:\mathrm{x}=\mathrm{50m}\:\:\mathrm{in}\:\mathrm{interval}\:\:\mathrm{15}\leqslant\mathrm{t}\leqslant\mathrm{33} \\ $$$$\:\:\:\:\:\mathrm{53}−\frac{\left(\mathrm{t}−\mathrm{24}\right)^{\mathrm{2}} }{\mathrm{3}}\:=\:\mathrm{50} \\ $$$$\Rightarrow\:\:\:\:\:\left(\mathrm{t}−\mathrm{24}\right)^{\mathrm{2}} \:=\:\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\mathrm{t}_{\mathrm{1}} =\:\mathrm{21s}\:\:\mathrm{and}\:\:\mathrm{t}_{\mathrm{2}} =\mathrm{27s}\:. \\ $$
Commented by ajfour last updated on 11/Jul/17
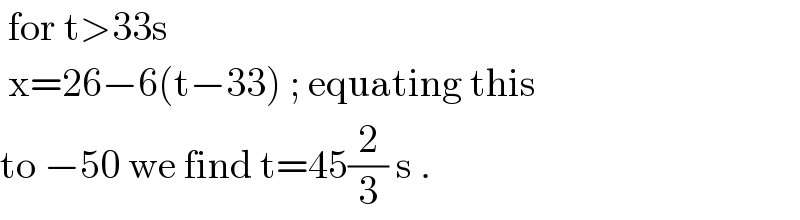
for t>33s x=26−6(t−33) ; equating this to −50 we find t=45(2/3) s .
$$\:\mathrm{for}\:\mathrm{t}>\mathrm{33s} \\ $$$$\:\mathrm{x}=\mathrm{26}−\mathrm{6}\left(\mathrm{t}−\mathrm{33}\right)\:;\:\mathrm{equating}\:\mathrm{this} \\ $$$$\mathrm{to}\:−\mathrm{50}\:\mathrm{we}\:\mathrm{find}\:\mathrm{t}=\mathrm{45}\frac{\mathrm{2}}{\mathrm{3}}\:\mathrm{s}\:. \\ $$
Commented by Tinkutara last updated on 11/Jul/17
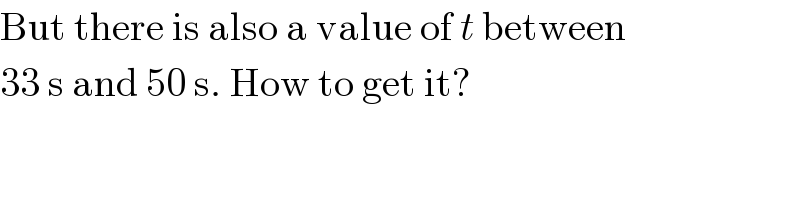
But there is also a value of t between 33 s and 50 s. How to get it?
$$\mathrm{But}\:\mathrm{there}\:\mathrm{is}\:\mathrm{also}\:\mathrm{a}\:\mathrm{value}\:\mathrm{of}\:{t}\:\mathrm{between} \\ $$$$\mathrm{33}\:\mathrm{s}\:\mathrm{and}\:\mathrm{50}\:\mathrm{s}.\:\mathrm{How}\:\mathrm{to}\:\mathrm{get}\:\mathrm{it}? \\ $$
Commented by Tinkutara last updated on 12/Jul/17
Thanks Sir!
$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *