Question-178697

Question Number 178697 by infinityaction last updated on 20/Oct/22

Commented by mr W last updated on 21/Oct/22

$${for}\:{a},{b},{c}\:\in\mathbb{R},\:{i}\:{think} \\ $$$${a}+{b}+{c}\leqslant\mathrm{2}\sqrt{\mathrm{3}} \\ $$

Commented by mr W last updated on 21/Oct/22

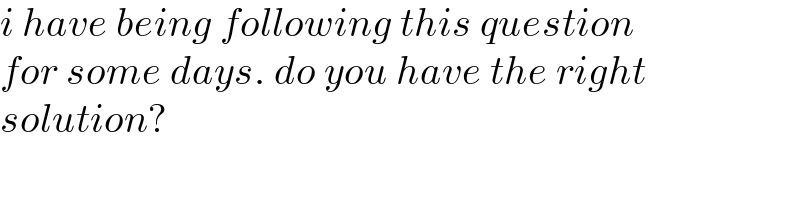
$${i}\:{have}\:{being}\:{following}\:{this}\:{question} \\ $$$${for}\:{some}\:{days}.\:{do}\:{you}\:{have}\:{the}\:{right} \\ $$$${solution}? \\ $$

Commented by mr W last updated on 21/Oct/22

i got the same result, as exact value. above i mistook (a+b+c)_(max) =2(√3). but it is only a local maximum from k^2 =λ=12. see solution below.

$${i}\:{got}\:{the}\:{same}\:{result},\:{as}\:{exact}\:{value}. \\ $$$${above}\:{i}\:{mistook}\:\left({a}+{b}+{c}\right)_{{max}} =\mathrm{2}\sqrt{\mathrm{3}}.\: \\ $$$${but}\:{it}\:{is}\:{only}\:{a}\:{local}\:{maximum}\:{from}\: \\ $$$${k}^{\mathrm{2}} =\lambda=\mathrm{12}.\: \\ $$$${see}\:{solution}\:{below}. \\ $$

Answered by mr W last updated on 22/Oct/22

(a+b+c)((1/a)+(1/b)+(1/c))−3=9 (a+b+c)(ab+bc+ca)=12abc let a+b+c=k abc=((k(ab+bc+ca))/(12)) (a+b+c)^2 =a^2 +b^2 +c^2 +2(ab+bc+ca) k^2 =12+2(ab+bc+ca) ab+bc+ca=((k^2 −12)/2) abc=((k(k^2 −12))/(24)) a,b,c are roots of following cubic eqn. z^3 −kz^2 +((k^2 −12)/2)z−((k(k^2 −12))/(24))=0 since a,b,c∈R, the eqn. must have three real roots. we transform it to t^3 +3pt+2q=0 with t=z−(k/3) p=((k^2 −36)/(18)) q=((k(11k^2 −324))/(432)) p^3 +q^2 ≤0 to get 3 real roots 32(k^2 −36)^3 +k^2 (11k^2 −324)^2 ≤0 let k^2 =λ (λ−12)(17λ^2 −972λ+13824)≤0 k_(max) ^2 =λ=((486+6(√(33)))/(17)) k_(max) =(√((486+6(√(33)))/(17))) i.e. (a+b+c)_(max) =(√((486+6(√(33)))/(17)))≈5.533148

$$\left({a}+{b}+{c}\right)\left(\frac{\mathrm{1}}{{a}}+\frac{\mathrm{1}}{{b}}+\frac{\mathrm{1}}{{c}}\right)−\mathrm{3}=\mathrm{9} \\ $$$$\left({a}+{b}+{c}\right)\left({ab}+{bc}+{ca}\right)=\mathrm{12}{abc} \\ $$$${let}\:{a}+{b}+{c}={k} \\ $$$${abc}=\frac{{k}\left({ab}+{bc}+{ca}\right)}{\mathrm{12}} \\ $$$$\left({a}+{b}+{c}\right)^{\mathrm{2}} ={a}^{\mathrm{2}} +{b}^{\mathrm{2}} +{c}^{\mathrm{2}} +\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$${k}^{\mathrm{2}} =\mathrm{12}+\mathrm{2}\left({ab}+{bc}+{ca}\right) \\ $$$${ab}+{bc}+{ca}=\frac{{k}^{\mathrm{2}} −\mathrm{12}}{\mathrm{2}} \\ $$$${abc}=\frac{{k}\left({k}^{\mathrm{2}} −\mathrm{12}\right)}{\mathrm{24}} \\ $$$${a},{b},{c}\:{are}\:{roots}\:{of}\:{following}\:{cubic}\:{eqn}. \\ $$$${z}^{\mathrm{3}} −{kz}^{\mathrm{2}} +\frac{{k}^{\mathrm{2}} −\mathrm{12}}{\mathrm{2}}{z}−\frac{{k}\left({k}^{\mathrm{2}} −\mathrm{12}\right)}{\mathrm{24}}=\mathrm{0} \\ $$$${since}\:{a},{b},{c}\in{R},\:{the}\:{eqn}.\:{must}\:{have} \\ $$$${three}\:{real}\:{roots}.\:{we}\:{transform}\:{it}\:{to} \\ $$$${t}^{\mathrm{3}} +\mathrm{3}{pt}+\mathrm{2}{q}=\mathrm{0}\:{with}\:{t}={z}−\frac{{k}}{\mathrm{3}} \\ $$$${p}=\frac{{k}^{\mathrm{2}} −\mathrm{36}}{\mathrm{18}} \\ $$$${q}=\frac{{k}\left(\mathrm{11}{k}^{\mathrm{2}} −\mathrm{324}\right)}{\mathrm{432}} \\ $$$${p}^{\mathrm{3}} +{q}^{\mathrm{2}} \leqslant\mathrm{0}\:{to}\:{get}\:\mathrm{3}\:{real}\:{roots} \\ $$$$\mathrm{32}\left({k}^{\mathrm{2}} −\mathrm{36}\right)^{\mathrm{3}} +{k}^{\mathrm{2}} \left(\mathrm{11}{k}^{\mathrm{2}} −\mathrm{324}\right)^{\mathrm{2}} \leqslant\mathrm{0} \\ $$$${let}\:{k}^{\mathrm{2}} =\lambda \\ $$$$\left(\lambda−\mathrm{12}\right)\left(\mathrm{17}\lambda^{\mathrm{2}} −\mathrm{972}\lambda+\mathrm{13824}\right)\leqslant\mathrm{0} \\ $$$${k}_{{max}} ^{\mathrm{2}} =\lambda=\frac{\mathrm{486}+\mathrm{6}\sqrt{\mathrm{33}}}{\mathrm{17}} \\ $$$${k}_{{max}} =\sqrt{\frac{\mathrm{486}+\mathrm{6}\sqrt{\mathrm{33}}}{\mathrm{17}}} \\ $$$${i}.{e}.\:\left({a}+{b}+{c}\right)_{{max}} =\sqrt{\frac{\mathrm{486}+\mathrm{6}\sqrt{\mathrm{33}}}{\mathrm{17}}}\approx\mathrm{5}.\mathrm{533148} \\ $$

Commented by infinityaction last updated on 22/Oct/22

$${thanks}\:{sir} \\ $$

Commented by Tawa11 last updated on 23/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply