Menu Close

Question-178712

Tinku Tara 0 Comments
Pin




Question Number 178712 by mnjuly1970 last updated on 20/Oct/22
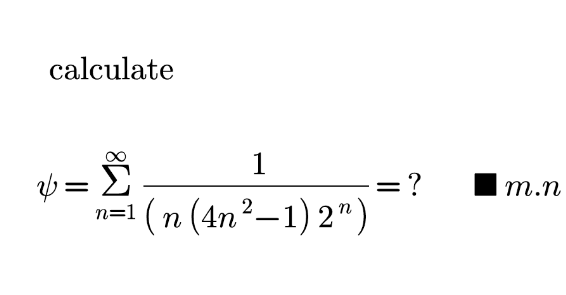
Answered by mr W last updated on 20/Oct/22
(1/n)((1/(4n^2 −1)))=(1/(2n))((1/(2n−1))−(1/(2n+1))) =(1/(2n−1))+(1/(2n+1))−(1/n) Σ_(n=1) ^∞ x^(2n) =(x^2 /(1−x^2 ))=(1/(1−x^2 ))−1 Σ_(n=1) ^∞ ∫_0 ^x x^(2n) dx=∫_0 ^x ((1/(1−x^2 ))−1)dx Σ_(n=1) ^∞ (x^(2n+1) /(2n+1))=(1/2)ln ((1+x)/(1−x))−x ⇒Σ_(n=1) ^∞ (x^(2n) /(2n+1))=(1/(2x))ln ((1+x)/(1−x))−1 with x=(1/( (√2)))<1 ⇒Σ_(n=1) ^∞ (1/((2n+1)2^n ))=((√2)/2)ln ((1+(1/( (√2))))/(1−(1/( (√2)))))−1=((√2)/2)ln (((√2)+1)/( (√2)−1))−1 Σ_(n=1) ^∞ x^(2n−2) =(1/(1−x^2 )) Σ_(n=1) ^∞ ∫_0 ^x x^(2n−2) dx=∫_0 ^x (dx/(1−x^2 )) Σ_(n=1) ^∞ (x^(2n−1) /(2n−1))=(1/2)ln ((1+x)/(1−x)) Σ_(n=1) ^∞ (x^(2n) /(2n−1))=(x/2)ln ((1+x)/(1−x)) with x=(1/( (√2)))<1 Σ_(n=1) ^∞ (1/((2n−1)2^n ))=(1/(2(√2)))ln ((1+(1/( (√2))))/(1−(1/( (√2)))))=((√2)/4)ln (((√2)+1)/( (√2)−1)) Σ_(n=1) ^∞ x^(n−1) =(1/(1−x)) Σ_(n=1) ^∞ ∫_0 ^x x^(n−1) dx=∫_0 ^x (dx/(1−x)) Σ_(n=1) ^∞ (x^n /n)=ln (1/(1−x)) with x=(1/2)<1 Σ_(n=1) ^∞ (1/(n2^n ))=ln (1/(1−(1/2)))=ln 2 Ψ=((√2)/2)ln (((√2)+1)/( (√2)−1))−1+((√2)/4)ln (((√2)+1)/( (√2)−1))−ln 2 =((3(√2))/2)ln ((√2)+1)−1−ln 2≈0.176528
$$\frac{\mathrm{1}}{{n}}\left(\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} −\mathrm{1}}\right)=\frac{\mathrm{1}}{\mathrm{2}{n}}\left(\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}{n}−\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}} \\ $$$$ \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{\mathrm{2}{n}} =\frac{{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{1} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{{x}} {x}^{\mathrm{2}{n}} {dx}=\int_{\mathrm{0}} ^{{x}} \left(\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }−\mathrm{1}\right){dx} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}+\mathrm{1}} }{\mathrm{2}{n}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}−{x} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{\mathrm{2}{n}+\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}{x}}\mathrm{ln}\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}−\mathrm{1} \\ $$$${with}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}<\mathrm{1} \\ $$$$\Rightarrow\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)\mathrm{2}^{{n}} }=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\frac{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}−\mathrm{1}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}−\mathrm{1} \\ $$$$ \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{\mathrm{2}{n}−\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{{x}} {x}^{\mathrm{2}{n}−\mathrm{2}} {dx}=\int_{\mathrm{0}} ^{{x}} \frac{{dx}}{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}−\mathrm{1}} }{\mathrm{2}{n}−\mathrm{1}}=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{ln}\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{\mathrm{2}{n}} }{\mathrm{2}{n}−\mathrm{1}}=\frac{{x}}{\mathrm{2}}\mathrm{ln}\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}} \\ $$$${with}\:{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}<\mathrm{1} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}{n}−\mathrm{1}\right)\mathrm{2}^{{n}} }=\frac{\mathrm{1}}{\mathrm{2}\sqrt{\mathrm{2}}}\mathrm{ln}\:\frac{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}{\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{ln}\:\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$$ \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{{x}} {x}^{{n}−\mathrm{1}} {dx}=\int_{\mathrm{0}} ^{{x}} \frac{{dx}}{\mathrm{1}−{x}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}}=\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$${with}\:{x}=\frac{\mathrm{1}}{\mathrm{2}}<\mathrm{1} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\mathrm{2}^{{n}} }=\mathrm{ln}\:\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}}=\mathrm{ln}\:\mathrm{2} \\ $$$$ \\ $$$$\Psi=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}−\mathrm{1}+\frac{\sqrt{\mathrm{2}}}{\mathrm{4}}\mathrm{ln}\:\frac{\sqrt{\mathrm{2}}+\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}−\mathrm{ln}\:\mathrm{2} \\ $$$$\:\:\:=\frac{\mathrm{3}\sqrt{\mathrm{2}}}{\mathrm{2}}\mathrm{ln}\:\left(\sqrt{\mathrm{2}}+\mathrm{1}\right)−\mathrm{1}−\mathrm{ln}\:\mathrm{2}\approx\mathrm{0}.\mathrm{176528} \\ $$
Commented by Tawa11 last updated on 20/Oct/22
Great sir
$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by mnjuly1970 last updated on 21/Oct/22
thanks alot sirW
$${thanks}\:{alot}\:{sirW} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *