Question-178833

Question Number 178833 by Spillover last updated on 22/Oct/22

Answered by cortano1 last updated on 22/Oct/22

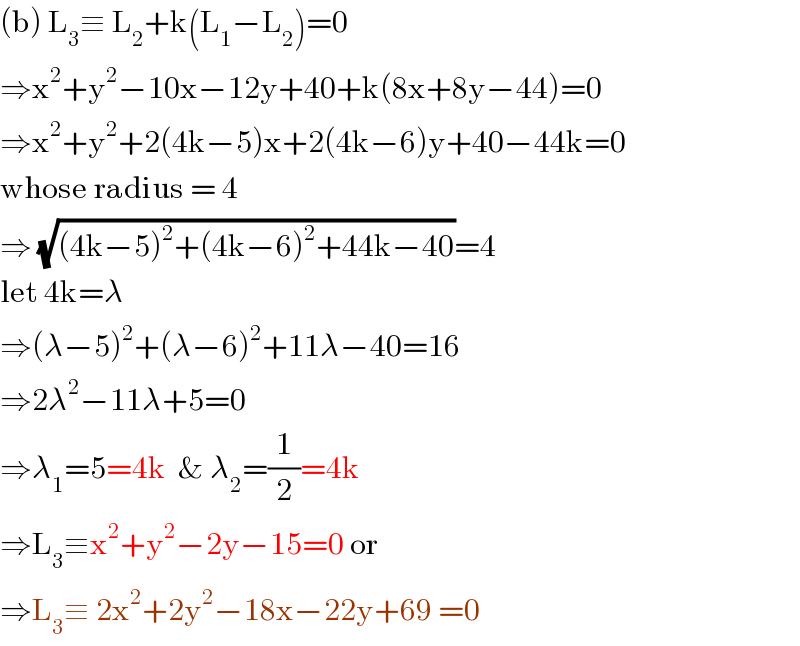
(b) L_3 ≡ L_2 +k(L_1 −L_2 )=0 ⇒x^2 +y^2 −10x−12y+40+k(8x+8y−44)=0 ⇒x^2 +y^2 +2(4k−5)x+2(4k−6)y+40−44k=0 whose radius = 4 ⇒ (√((4k−5)^2 +(4k−6)^2 +44k−40))=4 let 4k=λ ⇒(λ−5)^2 +(λ−6)^2 +11λ−40=16 ⇒2λ^2 −11λ+5=0 ⇒λ_1 =5=4k & λ_2 =(1/2)=4k ⇒L_3 ≡x^2 +y^2 −2y−15=0 or ⇒L_3 ≡ 2x^2 +2y^2 −18x−22y+69 =0

$$\left(\mathrm{b}\right)\:\mathrm{L}_{\mathrm{3}} \equiv\:\mathrm{L}_{\mathrm{2}} +\mathrm{k}\left(\mathrm{L}_{\mathrm{1}} −\mathrm{L}_{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{10x}−\mathrm{12y}+\mathrm{40}+\mathrm{k}\left(\mathrm{8x}+\mathrm{8y}−\mathrm{44}\right)=\mathrm{0} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} +\mathrm{2}\left(\mathrm{4k}−\mathrm{5}\right)\mathrm{x}+\mathrm{2}\left(\mathrm{4k}−\mathrm{6}\right)\mathrm{y}+\mathrm{40}−\mathrm{44k}=\mathrm{0} \\ $$$$\mathrm{whose}\:\mathrm{radius}\:=\:\mathrm{4} \\ $$$$\Rightarrow\:\sqrt{\left(\mathrm{4k}−\mathrm{5}\right)^{\mathrm{2}} +\left(\mathrm{4k}−\mathrm{6}\right)^{\mathrm{2}} +\mathrm{44k}−\mathrm{40}}=\mathrm{4} \\ $$$$\mathrm{let}\:\mathrm{4k}=\lambda \\ $$$$\Rightarrow\left(\lambda−\mathrm{5}\right)^{\mathrm{2}} +\left(\lambda−\mathrm{6}\right)^{\mathrm{2}} +\mathrm{11}\lambda−\mathrm{40}=\mathrm{16} \\ $$$$\Rightarrow\mathrm{2}\lambda^{\mathrm{2}} −\mathrm{11}\lambda+\mathrm{5}=\mathrm{0} \\ $$$$\Rightarrow\lambda_{\mathrm{1}} =\mathrm{5}=\mathrm{4k}\:\:\&\:\lambda_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{4k} \\ $$$$\Rightarrow\mathrm{L}_{\mathrm{3}} \equiv\mathrm{x}^{\mathrm{2}} +\mathrm{y}^{\mathrm{2}} −\mathrm{2y}−\mathrm{15}=\mathrm{0}\:\mathrm{or} \\ $$$$\Rightarrow\mathrm{L}_{\mathrm{3}} \equiv\:\mathrm{2x}^{\mathrm{2}} +\mathrm{2y}^{\mathrm{2}} −\mathrm{18x}−\mathrm{22y}+\mathrm{69}\:=\mathrm{0} \\ $$

Commented by cortano1 last updated on 22/Oct/22