Question-178839

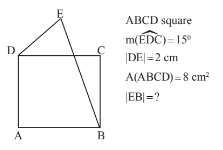
Question Number 178839 by ARUNG_Brandon_MBU last updated on 22/Oct/22

Answered by HeferH last updated on 22/Oct/22

Side of the square = (√8) = 2(√2) l_1 = 2(√2) −( (((√6) + (√2))/2))= ((3(√2) −(√6))/2) l_2 = 2(√2) + ((((√6) − (√2))/2))= ((3(√2) + (√6) )/2) l_1 ^( 2) + l_2 ^2 = EB^2 EB=(√(12)) = 2(√3)

$$\:{Side}\:{of}\:{the}\:{square}\:=\:\sqrt{\mathrm{8}}\:=\:\mathrm{2}\sqrt{\mathrm{2}} \\ $$$$\:{l}_{\mathrm{1}} =\:\mathrm{2}\sqrt{\mathrm{2}}\:−\left(\:\frac{\sqrt{\mathrm{6}}\:+\:\sqrt{\mathrm{2}}}{\mathrm{2}}\right)=\:\frac{\mathrm{3}\sqrt{\mathrm{2}}\:−\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$$\:{l}_{\mathrm{2}} =\:\mathrm{2}\sqrt{\mathrm{2}}\:+\:\left(\frac{\sqrt{\mathrm{6}}\:−\:\sqrt{\mathrm{2}}}{\mathrm{2}}\right)=\:\frac{\mathrm{3}\sqrt{\mathrm{2}}\:+\:\sqrt{\mathrm{6}}\:}{\mathrm{2}} \\ $$$$\:{l}_{\mathrm{1}} ^{\:\mathrm{2}} \:+\:{l}_{\mathrm{2}} \:^{\mathrm{2}} \:=\:{EB}^{\mathrm{2}} \\ $$$$\:{EB}=\sqrt{\mathrm{12}}\:=\:\mathrm{2}\sqrt{\mathrm{3}} \\ $$$$\: \\ $$$$\: \\ $$$$\: \\ $$

Commented by HeferH last updated on 22/Oct/22

Commented by ARUNG_Brandon_MBU last updated on 22/Oct/22

Thank you Sir

Commented by ARUNG_Brandon_MBU last updated on 22/Oct/22

Any explanations, please?

Commented by HeferH last updated on 22/Oct/22

Commented by ARUNG_Brandon_MBU last updated on 22/Oct/22

OK thanks. I get it now.

Commented by Rasheed.Sindhi last updated on 22/Oct/22

$${I}\:{didn}'{t}\:{get}\:{it}\:{sir},{please}\:{explain}\:{in}\: \\ $$$${some}\:{detail}. \\ $$

Commented by HeferH last updated on 22/Oct/22

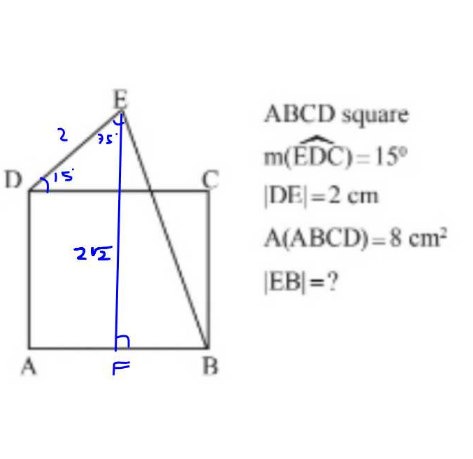
$${FE}:\:{l}_{\mathrm{2}} \\ $$$$\:{FB}:\:{l}_{\mathrm{1}} \\ $$$$\: \\ $$

Commented by Rasheed.Sindhi last updated on 23/Oct/22

Please execuse me for lack of fundamentals. Actually I can′t understand where the the values (√6) −(√2) &(√6) +(√2) have come from? And why your & my answers are different?

$${Please}\:{execuse}\:{me}\:{for}\:{lack}\:{of}\:{fundamentals}. \\ $$$${Actually}\:{I}\:{can}'{t}\:{understand}\:{where}\:{the} \\ $$$${the}\:{values}\:\sqrt{\mathrm{6}}\:−\sqrt{\mathrm{2}}\:\&\sqrt{\mathrm{6}}\:+\sqrt{\mathrm{2}}\:{have}\: \\ $$$${come}\:{from}?\:{And}\:{why}\:{your}\:\&\:{my} \\ $$$${answers}\:{are}\:{different}? \\ $$

Commented by Ar Brandon last updated on 23/Oct/22

They are the values of sin15° and cos15°, Sir. sin15°=(((√6)−(√2))/4) , cos15°=(((√6)+(√2))/4)

$$\mathrm{They}\:\mathrm{are}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{sin15}°\:\mathrm{and}\:\mathrm{cos15}°,\:\mathrm{Sir}. \\ $$$$\mathrm{sin15}°=\frac{\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}{\mathrm{4}}\:,\:\mathrm{cos15}°=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}} \\ $$

Commented by Rasheed.Sindhi last updated on 24/Oct/22

$$\mathrm{Ok},\:\mathrm{thanx}\:\mathrm{Brandon}\:\mathrm{sir}! \\ $$

Answered by Rasheed.Sindhi last updated on 22/Oct/22

■=s^2 =8;BD=(√(s^2 +s^2 ))=(√(8^2 +8^2 ))=8(√2) ∠BDE=45+15=60 △BDE: EB=(√(BD^2 +DE^2 −2BD∙DE∙cos∠BDE )) =(√((8(√2) )^2 +2^2 −2(8(√2) )(2)cos 60 )) =(√(128+4−2(8(√2) )(2)(1/2))) =(√(132−16(√2) )) =2(√(33−4(√2)))

$$\blacksquare={s}^{\mathrm{2}} =\mathrm{8};{BD}=\sqrt{{s}^{\mathrm{2}} +{s}^{\mathrm{2}} }=\sqrt{\mathrm{8}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} }=\mathrm{8}\sqrt{\mathrm{2}} \\ $$$$\angle{BDE}=\mathrm{45}+\mathrm{15}=\mathrm{60} \\ $$$$\bigtriangleup{BDE}: \\ $$$${EB}=\sqrt{{BD}^{\mathrm{2}} +{DE}^{\mathrm{2}} −\mathrm{2}{BD}\centerdot{DE}\centerdot\mathrm{cos}\angle{BDE}\:}\: \\ $$$$\:\:\:\:\:=\sqrt{\left(\mathrm{8}\sqrt{\mathrm{2}}\:\right)^{\mathrm{2}} +\mathrm{2}^{\mathrm{2}} −\mathrm{2}\left(\mathrm{8}\sqrt{\mathrm{2}}\:\right)\left(\mathrm{2}\right)\mathrm{cos}\:\mathrm{60}\:}\: \\ $$$$\:\:\:\:\:=\sqrt{\mathrm{128}+\mathrm{4}−\mathrm{2}\left(\mathrm{8}\sqrt{\mathrm{2}}\:\right)\left(\mathrm{2}\right)\left(\mathrm{1}/\mathrm{2}\right)}\: \\ $$$$\:\:\:\:\:=\sqrt{\mathrm{132}−\mathrm{16}\sqrt{\mathrm{2}}\:}\: \\ $$$$\:\:\:\:\:=\mathrm{2}\sqrt{\mathrm{33}−\mathrm{4}\sqrt{\mathrm{2}}}\: \\ $$

Commented by ARUNG_Brandon_MBU last updated on 22/Oct/22

Thank you Sir

Facebook Tweet Pin

Leave a Reply Cancel reply