Question-178922

Question Number 178922 by mnjuly1970 last updated on 22/Oct/22

Answered by ARUNG_Brandon_MBU last updated on 22/Oct/22

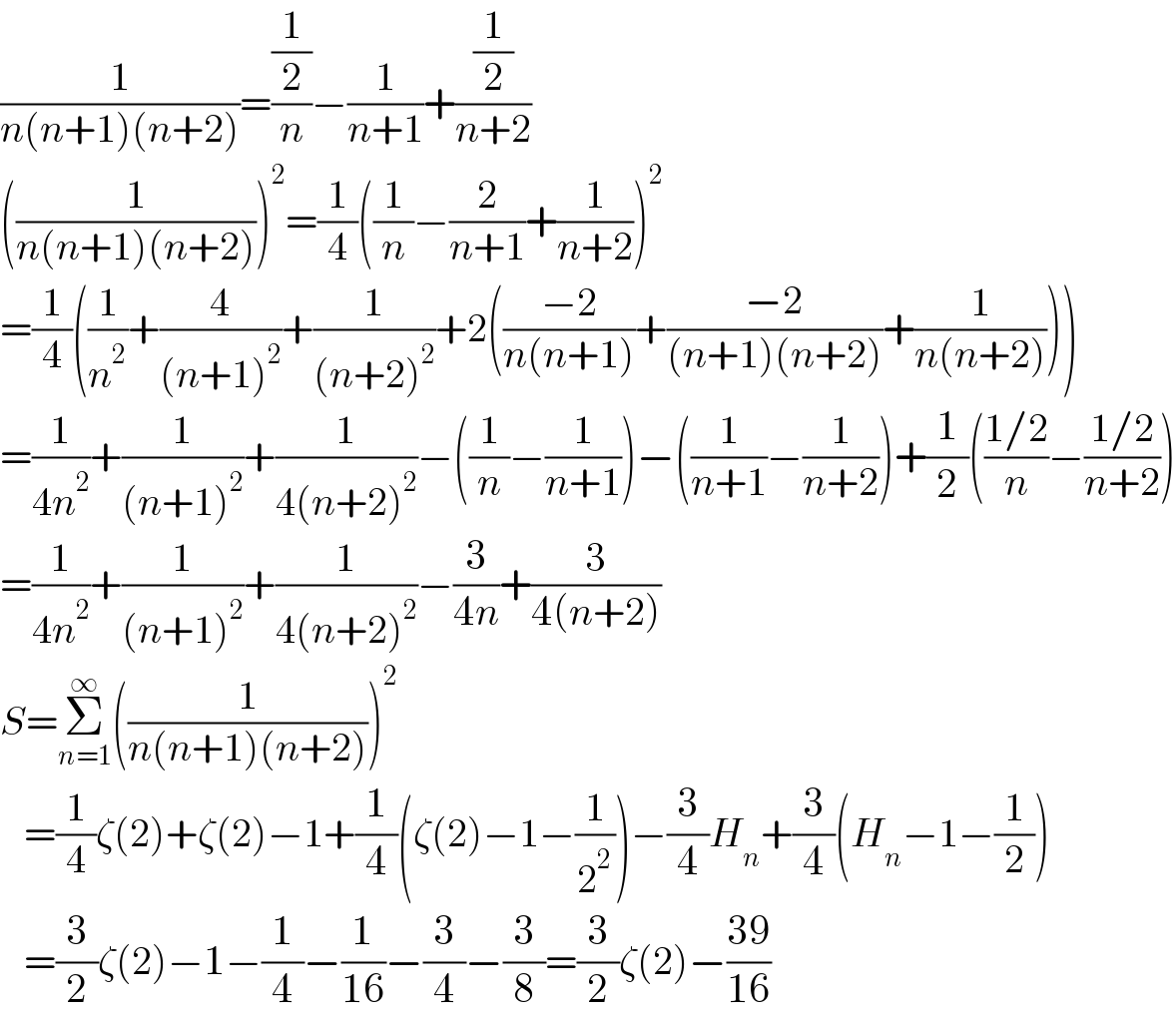
(1/(n(n+1)(n+2)))=((1/2)/n)−(1/(n+1))+((1/2)/(n+2)) ((1/(n(n+1)(n+2))))^2 =(1/4)((1/n)−(2/(n+1))+(1/(n+2)))^2 =(1/4)((1/n^2 )+(4/((n+1)^2 ))+(1/((n+2)^2 ))+2(((−2)/(n(n+1)))+((−2)/((n+1)(n+2)))+(1/(n(n+2))))) =(1/(4n^2 ))+(1/((n+1)^2 ))+(1/(4(n+2)^2 ))−((1/n)−(1/(n+1)))−((1/(n+1))−(1/(n+2)))+(1/2)(((1/2)/n)−((1/2)/(n+2))) =(1/(4n^2 ))+(1/((n+1)^2 ))+(1/(4(n+2)^2 ))−(3/(4n))+(3/(4(n+2))) S=Σ_(n=1) ^∞ ((1/(n(n+1)(n+2))))^2 =(1/4)ζ(2)+ζ(2)−1+(1/4)(ζ(2)−1−(1/2^2 ))−(3/4)H_n +(3/4)(H_n −1−(1/2)) =(3/2)ζ(2)−1−(1/4)−(1/(16))−(3/4)−(3/8)=(3/2)ζ(2)−((39)/(16))

$$\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}=\frac{\frac{\mathrm{1}}{\mathrm{2}}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}+\frac{\frac{\mathrm{1}}{\mathrm{2}}}{{n}+\mathrm{2}} \\ $$$$\left(\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\right)^{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{2}}{{n}+\mathrm{1}}+\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }+\frac{\mathrm{4}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{2}\right)^{\mathrm{2}} }+\mathrm{2}\left(\frac{−\mathrm{2}}{{n}\left({n}+\mathrm{1}\right)}+\frac{−\mathrm{2}}{\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}+\frac{\mathrm{1}}{{n}\left({n}+\mathrm{2}\right)}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}\left({n}+\mathrm{2}\right)^{\mathrm{2}} }−\left(\frac{\mathrm{1}}{{n}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right)−\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{1}/\mathrm{2}}{{n}}−\frac{\mathrm{1}/\mathrm{2}}{{n}+\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}{n}^{\mathrm{2}} }+\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{4}\left({n}+\mathrm{2}\right)^{\mathrm{2}} }−\frac{\mathrm{3}}{\mathrm{4}{n}}+\frac{\mathrm{3}}{\mathrm{4}\left({n}+\mathrm{2}\right)} \\ $$$${S}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}\left({n}+\mathrm{1}\right)\left({n}+\mathrm{2}\right)}\right)^{\mathrm{2}} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{4}}\zeta\left(\mathrm{2}\right)+\zeta\left(\mathrm{2}\right)−\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}\left(\zeta\left(\mathrm{2}\right)−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)−\frac{\mathrm{3}}{\mathrm{4}}{H}_{{n}} +\frac{\mathrm{3}}{\mathrm{4}}\left({H}_{{n}} −\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$\:\:\:=\frac{\mathrm{3}}{\mathrm{2}}\zeta\left(\mathrm{2}\right)−\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{16}}−\frac{\mathrm{3}}{\mathrm{4}}−\frac{\mathrm{3}}{\mathrm{8}}=\frac{\mathrm{3}}{\mathrm{2}}\zeta\left(\mathrm{2}\right)−\frac{\mathrm{39}}{\mathrm{16}} \\ $$

Commented by mnjuly1970 last updated on 22/Oct/22

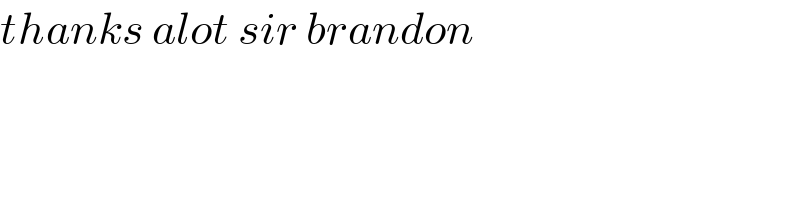
$${thanks}\:{alot}\:{sir}\:{brandon} \\ $$

Commented by Ar Brandon last updated on 23/Oct/22

You're welcome, Sir!

Commented by Tawa11 last updated on 23/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply