Question Number 178923 by mnjuly1970 last updated on 22/Oct/22

Commented by mr W last updated on 22/Oct/22

$$\frac{\mathrm{6}}{\:\sqrt[{\mathrm{6}}]{\mathrm{108}}}\:? \\ $$
Commented by Frix last updated on 22/Oct/22

$$\frac{\mathrm{6}}{\:\sqrt[{\mathrm{6}}]{\mathrm{108}}}=\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$
Commented by mr W last updated on 23/Oct/22
$${thanks}\:{for}\:{comfirming}! \\ $$
Answered by Frix last updated on 22/Oct/22
![let b=xa∧c=ya∧x, y >0 f(a, b, c)=(1/x)+((√x)/( (√y)))+(y)^(1/3) ((d[(1/x)+((√x)/( (√y)))+(y)^(1/3) ])/dx)=0 −(1/x^2 )+(1/(2(√(xy))))=0 ⇒ x=((4y))^(1/3) f(a, b, c)=(3/( ((4y))^(1/3) ))+(y)^(1/3) ((d[(3/( ((4y))^(1/3) ))+(y)^(1/3) ])/dy)=0 −(1/( ((4y^4 ))^(1/3) ))+(1/(3(y^2 )^(1/3) ))=0 ⇒ y=((3(√3))/2) ⇒ x=3^(1/2) 2^(1/3) ⇒ max (f) =3^(1/2) 2^(2/3)](https://www.tinkutara.com/question/Q178934.png)
$$\mathrm{let}\:{b}={xa}\wedge{c}={ya}\wedge{x},\:{y}\:>\mathrm{0} \\ $$$${f}\left({a},\:{b},\:{c}\right)=\frac{\mathrm{1}}{{x}}+\frac{\sqrt{{x}}}{\:\sqrt{{y}}}+\sqrt[{\mathrm{3}}]{{y}} \\ $$$$\frac{{d}\left[\frac{\mathrm{1}}{{x}}+\frac{\sqrt{{x}}}{\:\sqrt{{y}}}+\sqrt[{\mathrm{3}}]{{y}}\right]}{{dx}}=\mathrm{0} \\ $$$$−\frac{\mathrm{1}}{{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}\sqrt{{xy}}}=\mathrm{0}\:\Rightarrow\:{x}=\sqrt[{\mathrm{3}}]{\mathrm{4}{y}} \\ $$$${f}\left({a},\:{b},\:{c}\right)=\frac{\mathrm{3}}{\:\sqrt[{\mathrm{3}}]{\mathrm{4}{y}}}+\sqrt[{\mathrm{3}}]{{y}} \\ $$$$\frac{{d}\left[\frac{\mathrm{3}}{\:\sqrt[{\mathrm{3}}]{\mathrm{4}{y}}}+\sqrt[{\mathrm{3}}]{{y}}\right]}{{dy}}=\mathrm{0} \\ $$$$−\frac{\mathrm{1}}{\:\sqrt[{\mathrm{3}}]{\mathrm{4}{y}^{\mathrm{4}} }}+\frac{\mathrm{1}}{\mathrm{3}\sqrt[{\mathrm{3}}]{{y}^{\mathrm{2}} }}=\mathrm{0}\:\Rightarrow\:{y}=\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\Rightarrow\:{x}=\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} \\ $$$$\Rightarrow\:\mathrm{max}\:\left({f}\right)\:=\mathrm{3}^{\frac{\mathrm{1}}{\mathrm{2}}} \mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$
Answered by mr W last updated on 22/Oct/22
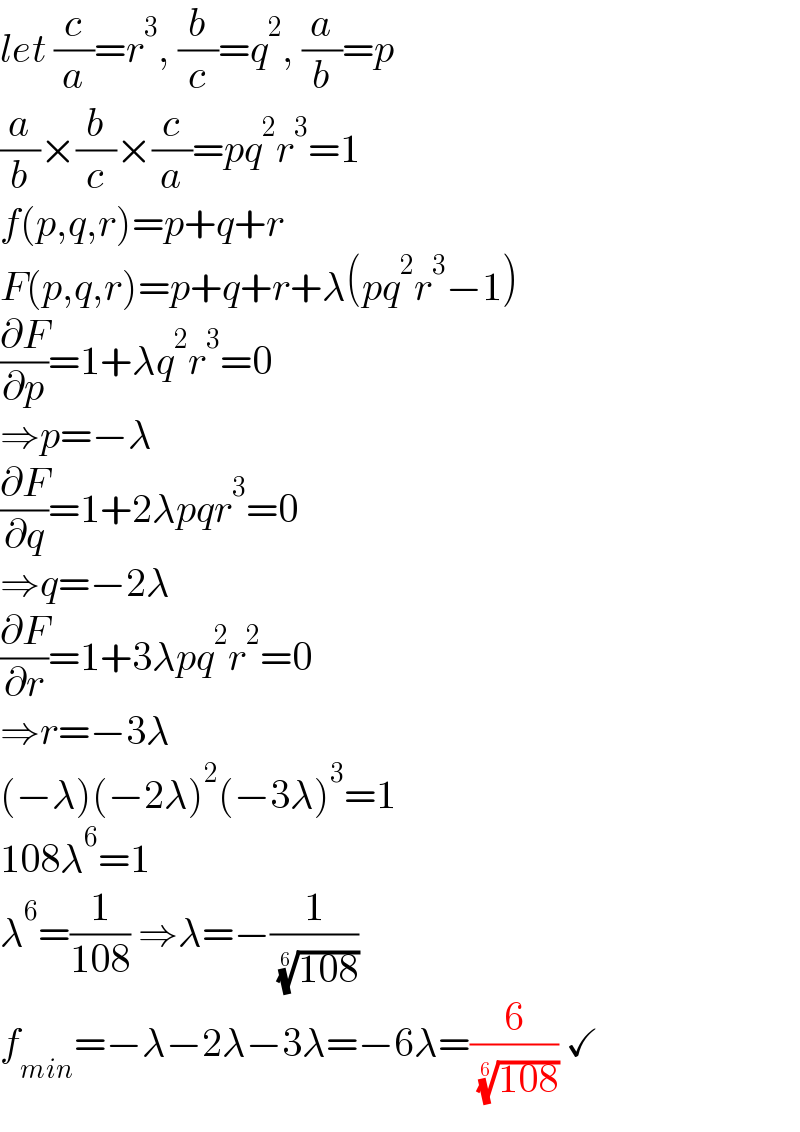
$${let}\:\frac{{c}}{{a}}={r}^{\mathrm{3}} ,\:\frac{{b}}{{c}}={q}^{\mathrm{2}} ,\:\frac{{a}}{{b}}={p} \\ $$$$\frac{{a}}{{b}}×\frac{{b}}{{c}}×\frac{{c}}{{a}}={pq}^{\mathrm{2}} {r}^{\mathrm{3}} =\mathrm{1} \\ $$$${f}\left({p},{q},{r}\right)={p}+{q}+{r} \\ $$$${F}\left({p},{q},{r}\right)={p}+{q}+{r}+\lambda\left({pq}^{\mathrm{2}} {r}^{\mathrm{3}} −\mathrm{1}\right) \\ $$$$\frac{\partial{F}}{\partial{p}}=\mathrm{1}+\lambda{q}^{\mathrm{2}} {r}^{\mathrm{3}} =\mathrm{0}\: \\ $$$$\Rightarrow{p}=−\lambda \\ $$$$\frac{\partial{F}}{\partial{q}}=\mathrm{1}+\mathrm{2}\lambda{pqr}^{\mathrm{3}} =\mathrm{0}\: \\ $$$$\Rightarrow{q}=−\mathrm{2}\lambda \\ $$$$\frac{\partial{F}}{\partial{r}}=\mathrm{1}+\mathrm{3}\lambda{pq}^{\mathrm{2}} {r}^{\mathrm{2}} =\mathrm{0}\: \\ $$$$\Rightarrow{r}=−\mathrm{3}\lambda \\ $$$$\left(−\lambda\right)\left(−\mathrm{2}\lambda\right)^{\mathrm{2}} \left(−\mathrm{3}\lambda\right)^{\mathrm{3}} =\mathrm{1} \\ $$$$\mathrm{108}\lambda^{\mathrm{6}} =\mathrm{1} \\ $$$$\lambda^{\mathrm{6}} =\frac{\mathrm{1}}{\mathrm{108}}\:\Rightarrow\lambda=−\frac{\mathrm{1}}{\:\sqrt[{\mathrm{6}}]{\mathrm{108}}} \\ $$$${f}_{{min}} =−\lambda−\mathrm{2}\lambda−\mathrm{3}\lambda=−\mathrm{6}\lambda=\frac{\mathrm{6}}{\:\sqrt[{\mathrm{6}}]{\mathrm{108}}}\:\checkmark \\ $$
