Question Number 178932 by cherokeesay last updated on 22/Oct/22
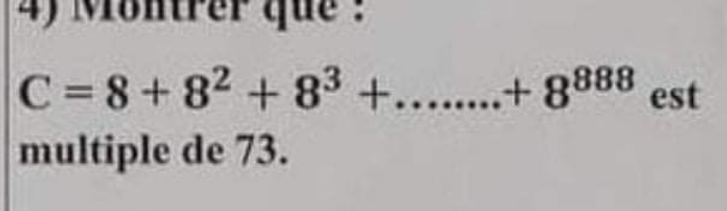
Answered by MJS_new last updated on 23/Oct/22

$${S}_{{n}} =\underset{{j}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{8}^{{j}} =\frac{\mathrm{8}}{\mathrm{7}}\left(\mathrm{8}^{{n}} −\mathrm{1}\right) \\ $$$${S}_{\mathrm{1}} =\mathrm{8}=\mathrm{0}×\mathrm{73}+\mathrm{8} \\ $$$${S}_{\mathrm{2}} =\mathrm{72}=\mathrm{1}×\mathrm{73}−\mathrm{1} \\ $$$${S}_{\mathrm{3}} =\mathrm{584}=\mathrm{8}×\mathrm{73} \\ $$$${S}_{\mathrm{4}} =\mathrm{4680}=\mathrm{64}×\mathrm{73}+\mathrm{8} \\ $$$${S}_{\mathrm{5}} =\mathrm{37448}=\mathrm{513}×\mathrm{73}−\mathrm{1} \\ $$$${S}_{\mathrm{6}} =\mathrm{299592}=\mathrm{4104}×\mathrm{73} \\ $$$$… \\ $$$${S}_{\mathrm{3}{k}−\mathrm{2}} /\mathrm{73}\:\Rightarrow\:\mathrm{remainder}\:\mathrm{8} \\ $$$${S}_{\mathrm{3}{k}−\mathrm{1}} /\mathrm{73}\:\Rightarrow\:\mathrm{remainder}\:−\mathrm{1} \\ $$$${S}_{\mathrm{3}{k}} /\mathrm{73}\:\Rightarrow\:\mathrm{remainder}\:\mathrm{0} \\ $$$${S}_{\mathrm{3}{k}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{73} \\ $$$${S}_{\mathrm{888}} ={S}_{\mathrm{3}×\mathrm{296}} \:\mathrm{is}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{73} \\ $$
Commented by cherokeesay last updated on 23/Oct/22

$${thank}\:{you}\:{so}\:{much}. \\ $$
