Question Number 178940 by ARUNG_Brandon_MBU last updated on 22/Oct/22
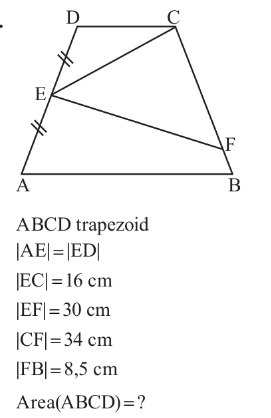
Answered by mr W last updated on 23/Oct/22

Commented by mr W last updated on 23/Oct/22
![ΔGEA≡ΔCED ⇒[ABCD]=[ΔGBC] CB=34+8.5=42.5 CG=2×16=32 cos α=((16^2 +34^2 −30^2 )/(2×16×34))=(8/(17)) ⇒sin α=(√(1−((8/(17)))^2 ))=((15)/(17)) [ΔGBC]=((CG×CB×sin α)/2) =((32×42.5×15)/(17×2))=600 ✓](https://www.tinkutara.com/question/Q178987.png)
$$\Delta{GEA}\equiv\Delta{CED} \\ $$$$\Rightarrow\left[{ABCD}\right]=\left[\Delta{GBC}\right] \\ $$$${CB}=\mathrm{34}+\mathrm{8}.\mathrm{5}=\mathrm{42}.\mathrm{5} \\ $$$${CG}=\mathrm{2}×\mathrm{16}=\mathrm{32} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{16}^{\mathrm{2}} +\mathrm{34}^{\mathrm{2}} −\mathrm{30}^{\mathrm{2}} }{\mathrm{2}×\mathrm{16}×\mathrm{34}}=\frac{\mathrm{8}}{\mathrm{17}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\sqrt{\mathrm{1}−\left(\frac{\mathrm{8}}{\mathrm{17}}\right)^{\mathrm{2}} }=\frac{\mathrm{15}}{\mathrm{17}} \\ $$$$\left[\Delta{GBC}\right]=\frac{{CG}×{CB}×\mathrm{sin}\:\alpha}{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\mathrm{32}×\mathrm{42}.\mathrm{5}×\mathrm{15}}{\mathrm{17}×\mathrm{2}}=\mathrm{600}\:\checkmark \\ $$
Commented by Ar Brandon last updated on 23/Oct/22
Thank you Sir
Commented by Tawa11 last updated on 23/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
