Question-178941

Question Number 178941 by ARUNG_Brandon_MBU last updated on 23/Oct/22

Commented by HeferH last updated on 23/Oct/22

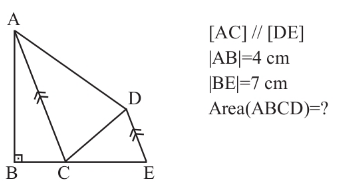
$${is}\:{AC}={DE}? \\ $$

Commented by Ar Brandon last updated on 23/Oct/22

No. They are given to be parallel.

Answered by som(math1967) last updated on 23/Oct/22

$${join}\:{AE}\: \\ $$$$\:{area}\:\bigtriangleup{ACD}={area}\bigtriangleup{AEC} \\ $$$$\left[{same}\:{base}\:{AC},\:{AC}\parallel{DE}\right] \\ $$$${area}\bigtriangleup{ABC}+\bigtriangleup{ACD}=\bigtriangleup{ABC}+\bigtriangleup{AEC} \\ $$$${area}\left({ABCD}\right)={area}\bigtriangleup{ABE} \\ $$$${area}\left({ABCD}\right)=\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{4}×\mathrm{7}=\mathrm{14}{cm}^{\mathrm{2}} \\ $$

Commented by som(math1967) last updated on 23/Oct/22

Commented by Ar Brandon last updated on 23/Oct/22

Thank you Sir

Commented by cortano1 last updated on 23/Oct/22

$$\mathrm{why}\:\mathrm{area}\:\Delta\mathrm{ACD}\:=\:\Delta\:\mathrm{ACE}\:? \\ $$

Commented by MJS_new last updated on 23/Oct/22

$$\mathrm{triangles}\:\mathrm{with}\:\mathrm{same}\:\mathrm{base}\:\mathrm{and}\:\mathrm{same}\:\mathrm{height} \\ $$$$\mathrm{have}\:\mathrm{same}\:\mathrm{area}.\:{AC}\:\mathrm{is}\:\mathrm{the}\:\mathrm{base}\:\mathrm{and}\:\mathrm{the}\:\mathrm{distance} \\ $$$$\mathrm{between}\:\mathrm{the}\:\mathrm{parallels}\:\mathrm{is}\:\mathrm{the}\:\mathrm{height} \\ $$

Commented by som(math1967) last updated on 23/Oct/22

$${they}\:{are}\:{in}\:{same}\:{base}\:{AC}\:{and} \\ $$$${between}\:{parallel}\:{AC}\:{and}\:{DE} \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com