Question-178947

Question Number 178947 by HeferH last updated on 23/Oct/22

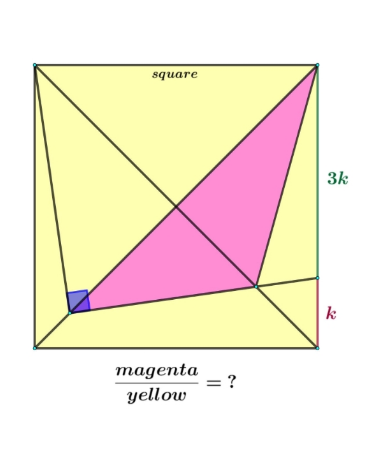
Answered by mr W last updated on 23/Oct/22

Commented by mr W last updated on 23/Oct/22

((sin β)/(4k))=((sin ((π/4)+β))/(GB)) ((sin α)/(3k))=((sin ((π/4)+α))/(GB)) ((3 sin β)/(4 sin α))=((sin ((π/4)+β))/(sin ((π/4)+α)))=((cos β+sin β)/(cos α+sin α)) α+β=(π/2) ((3 cos α)/(4 sin α))=1 ⇒tan α=(3/4) ((4k)/(sin β))=((GB)/(sin ((π/4)+β))) ⇒GB=((4k (cos β+sin β))/( (√2) sin β))=((7(√2)k)/( 2)) GH=GB−HB=((7(√2)k)/2)−((4(√2)k)/2)=((3(√2)k)/2) HE=GH tan α=((3(√2)k)/2)×(3/4)=((9(√2)k)/8) magenta area=((GB×HE)/2) =(1/2)×((7(√2)k)/( 2))×((9(√2)k)/8)=((63k^2 )/(16)) area of square =(4k)^2 =16k^2 yellow area=16k^2 −((63k^2 )/(16))=((193k^2 )/(16)) ((magenta)/(yellow))=((63)/(196)) ✓

$$\frac{\mathrm{sin}\:\beta}{\mathrm{4}{k}}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+\beta\right)}{{GB}} \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{3}{k}}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+\alpha\right)}{{GB}} \\ $$$$\frac{\mathrm{3}\:\mathrm{sin}\:\beta}{\mathrm{4}\:\mathrm{sin}\:\alpha}=\frac{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+\beta\right)}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+\alpha\right)}=\frac{\mathrm{cos}\:\beta+\mathrm{sin}\:\beta}{\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha} \\ $$$$\alpha+\beta=\frac{\pi}{\mathrm{2}} \\ $$$$\frac{\mathrm{3}\:\mathrm{cos}\:\alpha}{\mathrm{4}\:\mathrm{sin}\:\alpha}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{tan}\:\alpha=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$$\frac{\mathrm{4}{k}}{\mathrm{sin}\:\beta}=\frac{{GB}}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{4}}+\beta\right)} \\ $$$$\Rightarrow{GB}=\frac{\mathrm{4}{k}\:\left(\mathrm{cos}\:\beta+\mathrm{sin}\:\beta\right)}{\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\beta}=\frac{\mathrm{7}\sqrt{\mathrm{2}}{k}}{\:\mathrm{2}} \\ $$$${GH}={GB}−{HB}=\frac{\mathrm{7}\sqrt{\mathrm{2}}{k}}{\mathrm{2}}−\frac{\mathrm{4}\sqrt{\mathrm{2}}{k}}{\mathrm{2}}=\frac{\mathrm{3}\sqrt{\mathrm{2}}{k}}{\mathrm{2}} \\ $$$${HE}={GH}\:\mathrm{tan}\:\alpha=\frac{\mathrm{3}\sqrt{\mathrm{2}}{k}}{\mathrm{2}}×\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{9}\sqrt{\mathrm{2}}{k}}{\mathrm{8}} \\ $$$${magenta}\:{area}=\frac{{GB}×{HE}}{\mathrm{2}} \\ $$$$\:\:\:\:=\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{7}\sqrt{\mathrm{2}}{k}}{\:\mathrm{2}}×\frac{\mathrm{9}\sqrt{\mathrm{2}}{k}}{\mathrm{8}}=\frac{\mathrm{63}{k}^{\mathrm{2}} }{\mathrm{16}} \\ $$$${area}\:{of}\:{square}\:=\left(\mathrm{4}{k}\right)^{\mathrm{2}} =\mathrm{16}{k}^{\mathrm{2}} \\ $$$${yellow}\:{area}=\mathrm{16}{k}^{\mathrm{2}} −\frac{\mathrm{63}{k}^{\mathrm{2}} }{\mathrm{16}}=\frac{\mathrm{193}{k}^{\mathrm{2}} }{\mathrm{16}} \\ $$$$\frac{{magenta}}{{yellow}}=\frac{\mathrm{63}}{\mathrm{196}}\:\checkmark \\ $$

Commented by Tawa11 last updated on 23/Oct/22

$$\mathrm{Great}\:\mathrm{sir}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply