Question Number 178996 by Spillover last updated on 23/Oct/22

Answered by qaz last updated on 23/Oct/22
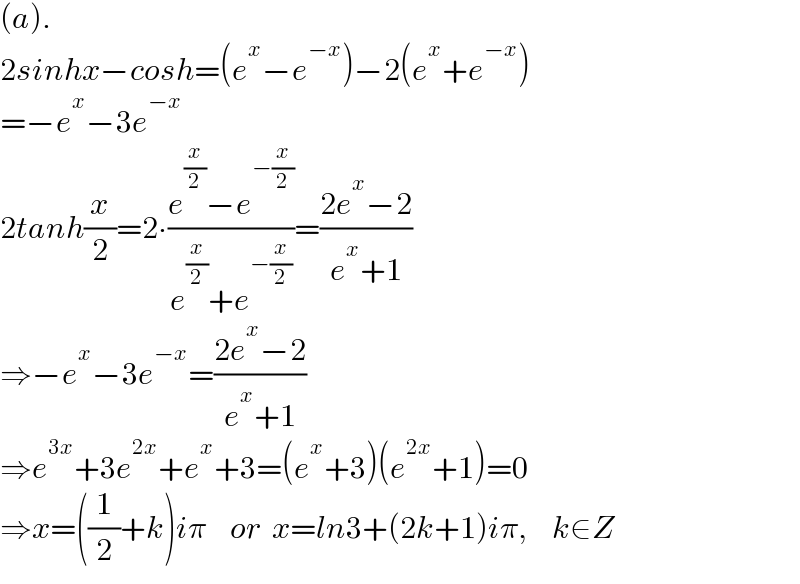
$$\left({a}\right). \\ $$$$\mathrm{2}{sinhx}−{cosh}=\left({e}^{{x}} −{e}^{−{x}} \right)−\mathrm{2}\left({e}^{{x}} +{e}^{−{x}} \right) \\ $$$$=−{e}^{{x}} −\mathrm{3}{e}^{−{x}} \\ $$$$\mathrm{2}{tanh}\frac{{x}}{\mathrm{2}}=\mathrm{2}\centerdot\frac{{e}^{\frac{{x}}{\mathrm{2}}} −{e}^{−\frac{{x}}{\mathrm{2}}} }{{e}^{\frac{{x}}{\mathrm{2}}} +{e}^{−\frac{{x}}{\mathrm{2}}} }=\frac{\mathrm{2}{e}^{{x}} −\mathrm{2}}{{e}^{{x}} +\mathrm{1}} \\ $$$$\Rightarrow−{e}^{{x}} −\mathrm{3}{e}^{−{x}} =\frac{\mathrm{2}{e}^{{x}} −\mathrm{2}}{{e}^{{x}} +\mathrm{1}} \\ $$$$\Rightarrow{e}^{\mathrm{3}{x}} +\mathrm{3}{e}^{\mathrm{2}{x}} +{e}^{{x}} +\mathrm{3}=\left({e}^{{x}} +\mathrm{3}\right)\left({e}^{\mathrm{2}{x}} +\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{x}=\left(\frac{\mathrm{1}}{\mathrm{2}}+{k}\right){i}\pi\:\:\:\:{or}\:\:{x}={ln}\mathrm{3}+\left(\mathrm{2}{k}+\mathrm{1}\right){i}\pi,\:\:\:\:{k}\in{Z} \\ $$
Answered by Frix last updated on 23/Oct/22
![2sinh x −cosh x =2tanh (x/2) e^x −e^(−x) −((e^x +e^(−x) )/2)=2((e^x −1)/(e^x +1)) e^(3x) −3e^(2x) +e^x −3=0 (e^x −3)(e^(2x) +1)=0 x=ln 3 16sinh^2 x cosh^2 x = =16(((e^x −e^(−x) )/2))^2 (((e^x +e^(−x) )/2))^3 = =((e^(5x) +e^(−5x) +e^(3x) +e^(−3x) −2e^x −2e^(−x) )/2)= =cosh 5x +cosh 3x −2cosh x 16∫_0 ^1 sinh^2 x cosh^2 x dx=^(t=e^x ) =∫_1 ^e ((t^4 /2)+(t^2 /2)−1−(1/t^2 )+(1/(2t^4 ))+(1/(2t^6 )))dt= =[(t^5 /(10))+(t^3 /6)−t+(1/t)−(1/(6t^3 ))−(1/(10t^5 ))]_1 ^e = =(e^5 /(10))+(e^3 /6)−e+(1/(tle))−(1/(6e^3 ))−(1/(10e^5 ))= =((sinh 5)/5)+((sinh 3)/3)−2sinh 1](https://www.tinkutara.com/question/Q179030.png)
$$\mathrm{2sinh}\:{x}\:−\mathrm{cosh}\:{x}\:=\mathrm{2tanh}\:\frac{{x}}{\mathrm{2}} \\ $$$$\mathrm{e}^{{x}} −\mathrm{e}^{−{x}} −\frac{\mathrm{e}^{{x}} +\mathrm{e}^{−{x}} }{\mathrm{2}}=\mathrm{2}\frac{\mathrm{e}^{{x}} −\mathrm{1}}{\mathrm{e}^{{x}} +\mathrm{1}} \\ $$$$\mathrm{e}^{\mathrm{3}{x}} −\mathrm{3e}^{\mathrm{2}{x}} +\mathrm{e}^{{x}} −\mathrm{3}=\mathrm{0} \\ $$$$\left(\mathrm{e}^{{x}} −\mathrm{3}\right)\left(\mathrm{e}^{\mathrm{2}{x}} +\mathrm{1}\right)=\mathrm{0} \\ $$$${x}=\mathrm{ln}\:\mathrm{3} \\ $$$$ \\ $$$$\mathrm{16sinh}^{\mathrm{2}} \:{x}\:\mathrm{cosh}^{\mathrm{2}} \:{x}\:= \\ $$$$=\mathrm{16}\left(\frac{\mathrm{e}^{{x}} −\mathrm{e}^{−{x}} }{\mathrm{2}}\right)^{\mathrm{2}} \left(\frac{\mathrm{e}^{{x}} +\mathrm{e}^{−{x}} }{\mathrm{2}}\right)^{\mathrm{3}} = \\ $$$$=\frac{\mathrm{e}^{\mathrm{5}{x}} +\mathrm{e}^{−\mathrm{5}{x}} +\mathrm{e}^{\mathrm{3}{x}} +\mathrm{e}^{−\mathrm{3}{x}} −\mathrm{2e}^{{x}} −\mathrm{2e}^{−{x}} }{\mathrm{2}}= \\ $$$$=\mathrm{cosh}\:\mathrm{5}{x}\:+\mathrm{cosh}\:\mathrm{3}{x}\:−\mathrm{2cosh}\:{x} \\ $$$$ \\ $$$$\mathrm{16}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\mathrm{sinh}^{\mathrm{2}} \:{x}\:\mathrm{cosh}^{\mathrm{2}} \:{x}\:{dx}\overset{{t}=\mathrm{e}^{{x}} } {=} \\ $$$$=\underset{\mathrm{1}} {\overset{\mathrm{e}} {\int}}\left(\frac{{t}^{\mathrm{4}} }{\mathrm{2}}+\frac{{t}^{\mathrm{2}} }{\mathrm{2}}−\mathrm{1}−\frac{\mathrm{1}}{{t}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{2}{t}^{\mathrm{6}} }\right){dt}= \\ $$$$=\left[\frac{{t}^{\mathrm{5}} }{\mathrm{10}}+\frac{{t}^{\mathrm{3}} }{\mathrm{6}}−{t}+\frac{\mathrm{1}}{{t}}−\frac{\mathrm{1}}{\mathrm{6}{t}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{10}{t}^{\mathrm{5}} }\right]_{\mathrm{1}} ^{\mathrm{e}} = \\ $$$$=\frac{\mathrm{e}^{\mathrm{5}} }{\mathrm{10}}+\frac{\mathrm{e}^{\mathrm{3}} }{\mathrm{6}}−\mathrm{e}+\frac{\mathrm{1}}{{t}\mathrm{le}}−\frac{\mathrm{1}}{\mathrm{6e}^{\mathrm{3}} }−\frac{\mathrm{1}}{\mathrm{10e}^{\mathrm{5}} }= \\ $$$$=\frac{\mathrm{sinh}\:\mathrm{5}}{\mathrm{5}}+\frac{\mathrm{sinh}\:\mathrm{3}}{\mathrm{3}}−\mathrm{2sinh}\:\mathrm{1} \\ $$
