Question Number 17901 by chux last updated on 12/Jul/17
Commented by chux last updated on 12/Jul/17
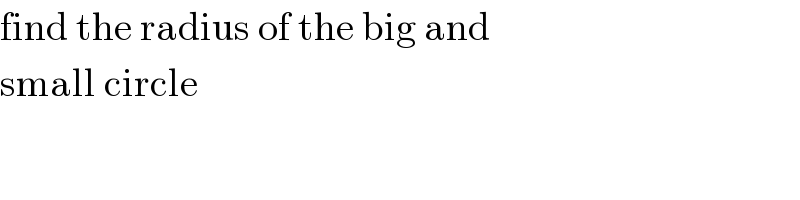
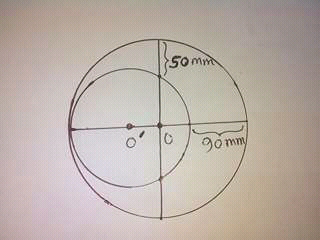
$$\mathrm{find}\:\mathrm{the}\:\mathrm{radius}\:\mathrm{of}\:\mathrm{the}\:\mathrm{big}\:\mathrm{and} \\ $$$$\mathrm{small}\:\mathrm{circle} \\ $$
Commented by chux last updated on 12/Jul/17

$$\mathrm{yes},\mathrm{they}\:\mathrm{are} \\ $$
Answered by mrW1 last updated on 12/Jul/17
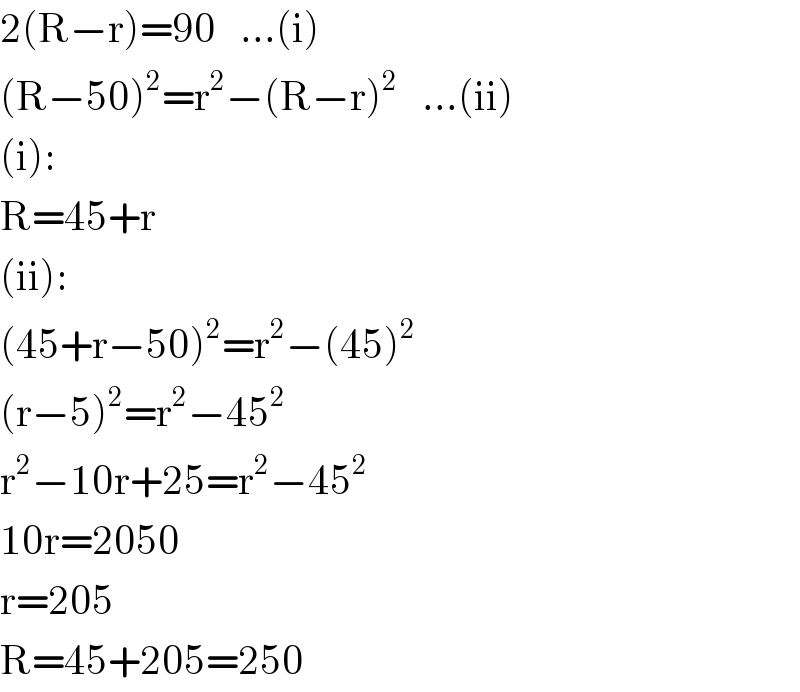
$$\mathrm{2}\left(\mathrm{R}−\mathrm{r}\right)=\mathrm{90}\:\:\:…\left(\mathrm{i}\right) \\ $$$$\left(\mathrm{R}−\mathrm{50}\right)^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} −\left(\mathrm{R}−\mathrm{r}\right)^{\mathrm{2}} \:\:\:…\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right): \\ $$$$\mathrm{R}=\mathrm{45}+\mathrm{r} \\ $$$$\left(\mathrm{ii}\right): \\ $$$$\left(\mathrm{45}+\mathrm{r}−\mathrm{50}\right)^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} −\left(\mathrm{45}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{r}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{r}^{\mathrm{2}} −\mathrm{45}^{\mathrm{2}} \\ $$$$\mathrm{r}^{\mathrm{2}} −\mathrm{10r}+\mathrm{25}=\mathrm{r}^{\mathrm{2}} −\mathrm{45}^{\mathrm{2}} \\ $$$$\mathrm{10r}=\mathrm{2050} \\ $$$$\mathrm{r}=\mathrm{205} \\ $$$$\mathrm{R}=\mathrm{45}+\mathrm{205}=\mathrm{250} \\ $$
Commented by chux last updated on 12/Jul/17

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
