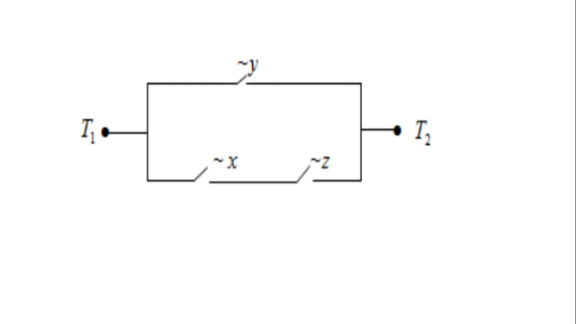
Question Number 179018 by Spillover last updated on 23/Oct/22

Answered by Tokugami last updated on 26/Oct/22

$$\begin{array}{|c|c|c|c|c|c|c|c|c|}{{x}}&\hline{{y}}&\hline{{z}}&\hline{{p}}\\{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}\\{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}\\{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}\\{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}\\{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}\\{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}\\{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}\\{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}&\hline{\mathrm{1}}\\\hline\end{array} \\ $$$${p}=\left({x}\:\mathrm{nor}\:{y}\right)\:\mathrm{or}\:\left({y}\:\mathrm{nor}\:{z}\right)\:\mathrm{or}\:\left({z}\:\mathrm{nor}\:{x}\right) \\ $$$$\mathrm{just}\:\mathrm{draw}\:\mathrm{a}\:\mathrm{diagram}\:\mathrm{from}\:\mathrm{that}. \\ $$
Answered by Spillover last updated on 27/Oct/22

Answered by Spillover last updated on 27/Oct/22