Question Number 179088 by cortano1 last updated on 24/Oct/22
Answered by mr W last updated on 24/Oct/22

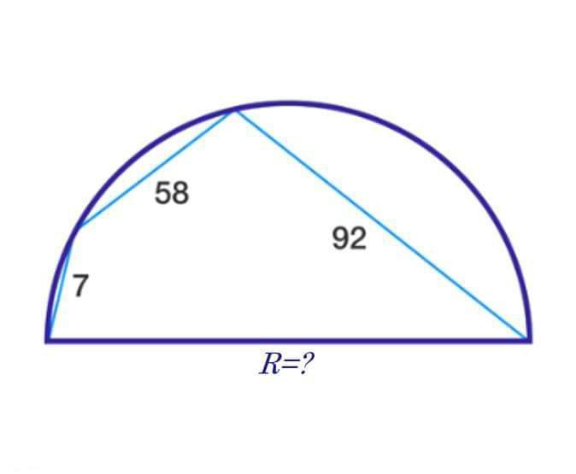
$$\boldsymbol{{Method}}\:\mathrm{1} \\ $$$$\mathrm{cos}\:\alpha=\frac{\mathrm{7}}{{R}} \\ $$$${R}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} =\mathrm{58}^{\mathrm{2}} +\mathrm{92}^{\mathrm{2}} +\mathrm{2}×\mathrm{58}×\mathrm{92}×\frac{\mathrm{7}}{{R}} \\ $$$${R}^{\mathrm{3}} −\mathrm{11877}{R}−\mathrm{71704}=\mathrm{0} \\ $$$${R}=\mathrm{2}\sqrt{\mathrm{3959}}\:\mathrm{sin}\:\left(\frac{\mathrm{2}\pi}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{35852}}{\mathrm{3959}\sqrt{\mathrm{3959}}}\right) \\ $$$$\:\:\:\:\approx\mathrm{112}.\mathrm{095} \\ $$
Commented by cortano1 last updated on 25/Oct/22

$$\mathrm{not}\:\mathrm{R}\:=\:\mathrm{56}\:\mathrm{sir}\:? \\ $$
Commented by mr W last updated on 25/Oct/22

$${R}\:{is}\:{shown}\:{as}\:{diameter}. \\ $$
Answered by mr W last updated on 24/Oct/22

$$\boldsymbol{{Method}}\:\mathrm{2} \\ $$$$\sqrt{\left({R}^{\mathrm{2}} −\mathrm{7}^{\mathrm{2}} \right)\left({R}^{\mathrm{2}} −\mathrm{92}^{\mathrm{2}} \right)}=\mathrm{7}×\mathrm{92}+\mathrm{58}{R} \\ $$$${R}^{\mathrm{4}} −\left(\mathrm{7}^{\mathrm{2}} +\mathrm{92}^{\mathrm{2}} \right){R}^{\mathrm{2}} +\mathrm{7}^{\mathrm{2}} ×\mathrm{92}^{\mathrm{2}} =\mathrm{7}^{\mathrm{2}} ×\mathrm{92}^{\mathrm{2}} +\mathrm{58}^{\mathrm{2}} {R}^{\mathrm{2}} +\mathrm{2}×\mathrm{7}×\mathrm{92}×\mathrm{58}{R} \\ $$$${R}^{\mathrm{3}} −\left(\mathrm{7}^{\mathrm{2}} +\mathrm{92}^{\mathrm{2}} +\mathrm{58}^{\mathrm{2}} \right){R}−\mathrm{2}×\mathrm{7}×\mathrm{92}×\mathrm{58}=\mathrm{0} \\ $$$${R}^{\mathrm{3}} −\mathrm{11877}{R}−\mathrm{71704}=\mathrm{0} \\ $$$${the}\:{rest}\:{see}\:{above}. \\ $$
