Question Number 179955 by Shrinava last updated on 04/Nov/22
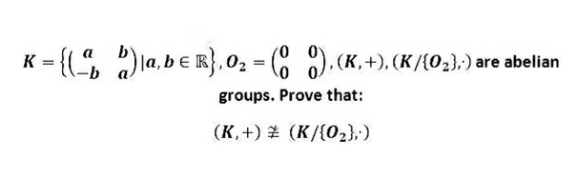
Answered by aleks041103 last updated on 04/Nov/22

$$\left({K},+\right)\ncong\left({K}/\left\{{O}_{\mathrm{2}} \right\},\:\centerdot\right)\Rightarrow \\ $$$$\nexists{s}:{K}\rightarrow{K}/\left\{{O}_{\mathrm{2}} \right\}:{s}\left({x}+{y}\right)={s}\left({x}\right)\centerdot{s}\left({y}\right)\wedge{s}−{bijective} \\ $$$${denote}\:\begin{pmatrix}{{a}}&{{b}}\\{−{b}}&{{a}}\end{pmatrix}\::=\left({a},{b}\right) \\ $$$${then}\:\left({a},{b}\right)+\left({c},{d}\right)=\left({a}+{c},{b}+{d}\right) \\ $$$$\left({a},{b}\right)\centerdot\left({c},{d}\right)=\begin{pmatrix}{{a}}&{{b}}\\{−{b}}&{{a}}\end{pmatrix}\:\centerdot\begin{pmatrix}{{c}}&{{d}}\\{−{d}}&{{c}}\end{pmatrix}\:= \\ $$$$=\begin{pmatrix}{{ac}−{bd}}&{{ad}+{bc}}\\{−\left({ad}+{bc}\right)}&{{ac}−{bd}}\end{pmatrix}\:=\:\left({ac}−{bd},{ad}+{bc}\right) \\ $$$${But}\:{for}\:{complex}\:{numbers}\:{we}\:{have} \\ $$$$\left({a}+{bi}\right)+\left({c}+{di}\right)=\left({a}+{c}\right)+\left({b}+{d}\right){i} \\ $$$${and} \\ $$$$\left({a}+{bi}\right)\left({c}+{di}\right)=\left({ac}−{bd}\right)+{i}\left({ad}+{bc}\right) \\ $$$$\Rightarrow{obviously}\left({if}\:{this}\:{is}\:{not}\:{obvious},\:{I}'{ll}\:{clarify}\:−\:{just}\:{ask}\right) \\ $$$$\left({K},+\right)\cong\left(\mathbb{C},+\right)\:{and}\:\left({K}/\left\{{O}_{\mathrm{2}} \right\},\centerdot\right)\cong\left(\mathbb{C}/\left\{\mathrm{0}\right\},\centerdot\right) \\ $$$${Therefore}\:{to}\:{prove}\:{that}\:\left({K},+\right)\ncong\left({K}/\left\{{O}_{\mathrm{2}} \right\},\:\centerdot\right) \\ $$$${is}\:{equivalent}\:{to}\:{proving}\:{that} \\ $$$$\left(\mathbb{C},+\right)\ncong\left(\mathbb{C}/\left\{\mathrm{0}\right\},\:\centerdot\right). \\ $$$${suppose}\:\left(\mathbb{C},+\right)\cong\left(\mathbb{C}/\left\{\mathrm{0}\right\},\:\centerdot\right). \\ $$$${then}\:\exists{s}:\mathbb{C}\rightarrow\mathbb{C}/\left\{\mathrm{0}\right\}:{s}\left({z}+{w}\right)={s}\left({z}\right){s}\left({w}\right) \\ $$$${and}\:\exists{s}^{−\mathrm{1}} :\mathbb{C}/\left\{\mathrm{0}\right\}\rightarrow\mathbb{C}:{s}\left({s}^{−\mathrm{1}} \left({z}\right)\right)={z}\:{and}\:{s}^{−\mathrm{1}} \left({s}\left({z}\right)\right)={z} \\ $$$${but}\:{if}\:{s}\left({z}+{w}\right)={s}\left({z}\right){s}\left({w}\right)\Rightarrow{s}\left({z}\right)={v}^{{z}} ,\:{for}\:{some}\:{v}\in\mathbb{C}/\left\{\mathrm{0}\right\} \\ $$$$\Rightarrow{v}={re}^{\mathrm{2}\pi{if}} ,\:{r}\in\mathbb{R}^{+} \:{and}\:{f}\in\left[\mathrm{0},\mathrm{1}\right) \\ $$$$\Rightarrow{s}\left({a}+{bi}\right)={r}^{{a}} {e}^{−\mathrm{2}\pi{bf}} \left({r}^{{ib}} {e}^{\mathrm{2}\pi{ifa}} \right)={e}^{{a}\:{ln}\left({r}\right)−\mathrm{2}\pi{bf}} {e}^{{i}\left(\mathrm{2}\pi{fa}+{b}\:{ln}\left({r}\right)\right)} \\ $$$${now}\:{we}\:{need}\:{to}\:{find}\:\left({a},{b}\right)\:{for}\:{given}\:{s}\left({a}+{bi}\right)={e}^{{u}} {e}^{{i}\left({p}+\mathrm{2}{k}\pi\right)} , \\ $$$${where}\:{u}\in\mathbb{R}^{+} \:{and}\:{p}\in\left[\mathrm{0},\mathrm{2}\pi\right). \\ $$$$\Rightarrow \\ $$$$\begin{cases}{{aln}\left({r}\right)−\mathrm{2}\pi{bf}={u}}\\{{bln}\left({r}\right)+\mathrm{2}\pi{af}={p}+\mathrm{2}{k}\pi}\end{cases} \\ $$$${i}.{e}. \\ $$$$\begin{pmatrix}{{ln}\left({r}\right)}&{−\mathrm{2}\pi{f}}\\{\mathrm{2}\pi{f}}&{{ln}\left({r}\right)}\end{pmatrix}\:\begin{pmatrix}{{a}}\\{{b}}\end{pmatrix}\:=\begin{pmatrix}{{u}}\\{{p}+\mathrm{2}{k}\pi}\end{pmatrix} \\ $$$${but}\:{det}\left(\begin{pmatrix}{{ln}\left({r}\right)}&{−\mathrm{2}\pi{f}}\\{\mathrm{2}\pi{f}}&{{ln}\left({r}\right)}\end{pmatrix}\right)=\left({ln}\left({r}\right)\right)^{\mathrm{2}} +\mathrm{4}\pi^{\mathrm{2}} {f}^{\mathrm{2}} >\mathrm{0} \\ $$$$\Rightarrow{we}\:{can}\:{always}\:{invert}\:{the}\:{matrix}\:{and}\:{find} \\ $$$$\left({a},{b}\right)\:{for}\:\forall{k}\in\mathbb{Z}. \\ $$$$\Rightarrow{if}\:{s}:\mathbb{C}\rightarrow\mathbb{C}/\left\{\mathrm{0}\right\}\::\:{s}\left({z}+{w}\right)={s}\left({z}\right){s}\left({w}\right) \\ $$$${then}\:{for}\:\forall{w}\in\mathbb{C}/\left\{\mathrm{0}\right\},\:\exists{z}_{\mathrm{1}} \neq{z}_{\mathrm{2}} \left({z}_{\mathrm{1},\mathrm{2}} \in\mathbb{C}\right):{s}\left({z}_{\mathrm{1}} \right)={s}\left({z}_{\mathrm{2}} \right) \\ $$$$\Rightarrow{s}\:{is}\:{not}\:{bijective} \\ $$$$\Rightarrow\:{every}\:{homomorphism}\:{from}\:\left(\mathbb{C},+\right)\:{to}\: \\ $$$$\left(\mathbb{C}/\left\{\mathrm{0}\right\},\centerdot\right)\:{is}\:{not}\:{bijective}. \\ $$$$\Rightarrow\left({K},+\right)\cong\left(\mathbb{C},+\right)\:\ncong\left(\mathbb{C}/\left\{\mathrm{0}\right\},\centerdot\right)\cong\left({K}/\left\{{O}_{\mathrm{2}} \right\},\centerdot\right) \\ $$$$\Rightarrow\left({K},+\right)\ncong\left({K}/\left\{{O}_{\mathrm{2}} \right\},\centerdot\right) \\ $$$${Q}.{E}.{D} \\ $$
Commented by Shrinava last updated on 05/Nov/22
$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
