Question Number 18004 by ajfour last updated on 13/Jul/17
Commented by ajfour last updated on 13/Jul/17

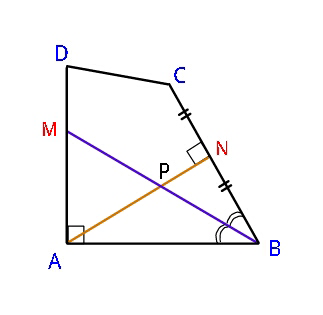
$$\mathrm{The}\:\mathrm{angular}\:\mathrm{bisector}\:\mathrm{of}\:\angle\mathrm{ABC} \\ $$$$\mathrm{intersects}\:\mathrm{side}\:\mathrm{AD}\:\mathrm{at}\:\mathrm{point}\:\mathrm{M},\:\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{perpendicular}\:\mathrm{dropped}\:\mathrm{from} \\ $$$$\mathrm{vertex}\:\mathrm{A}\:\mathrm{to}\:\mathrm{side}\:\mathrm{BC}\:\mathrm{cuts}\:\mathrm{BC}\:\mathrm{at} \\ $$$$\mathrm{point}\:\mathrm{N}\:\mathrm{so}\:\mathrm{that}\:\mathrm{BN}=\mathrm{NC}\:\mathrm{and} \\ $$$$\mathrm{AM}=\mathrm{2MD}.\:\mathrm{Find}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{and}\:\mathrm{area} \\ $$$$\mathrm{S}\:\mathrm{of}\:\mathrm{the}\:\mathrm{convex}\:\mathrm{quadrilateral} \\ $$$$\mathrm{ABCD}\:\mathrm{if}\:\mathrm{the}\:\mathrm{perimeter}\:\mathrm{is}\:\mathrm{equal}\:\mathrm{to} \\ $$$$\mathrm{5}+\sqrt{\mathrm{3}}\:,\:\angle\mathrm{BAD}=\mathrm{90}°,\:\angle\mathrm{ABC}=\mathrm{60}°\:. \\ $$
Answered by mrW1 last updated on 14/Jul/17
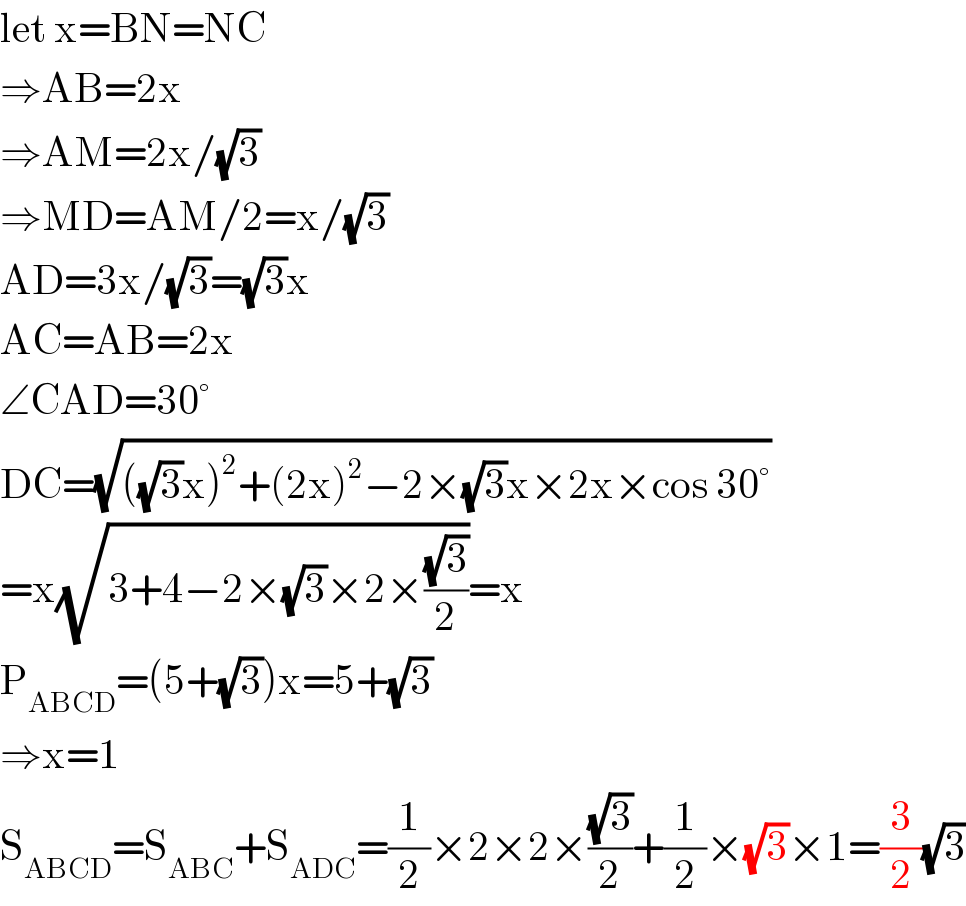
$$\mathrm{let}\:\mathrm{x}=\mathrm{BN}=\mathrm{NC} \\ $$$$\Rightarrow\mathrm{AB}=\mathrm{2x} \\ $$$$\Rightarrow\mathrm{AM}=\mathrm{2x}/\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{MD}=\mathrm{AM}/\mathrm{2}=\mathrm{x}/\sqrt{\mathrm{3}} \\ $$$$\mathrm{AD}=\mathrm{3x}/\sqrt{\mathrm{3}}=\sqrt{\mathrm{3}}\mathrm{x} \\ $$$$\mathrm{AC}=\mathrm{AB}=\mathrm{2x} \\ $$$$\angle\mathrm{CAD}=\mathrm{30}° \\ $$$$\mathrm{DC}=\sqrt{\left(\sqrt{\mathrm{3}}\mathrm{x}\right)^{\mathrm{2}} +\left(\mathrm{2x}\right)^{\mathrm{2}} −\mathrm{2}×\sqrt{\mathrm{3}}\mathrm{x}×\mathrm{2x}×\mathrm{cos}\:\mathrm{30}°} \\ $$$$=\mathrm{x}\sqrt{\mathrm{3}+\mathrm{4}−\mathrm{2}×\sqrt{\mathrm{3}}×\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}}=\mathrm{x} \\ $$$$\mathrm{P}_{\mathrm{ABCD}} =\left(\mathrm{5}+\sqrt{\mathrm{3}}\right)\mathrm{x}=\mathrm{5}+\sqrt{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{x}=\mathrm{1} \\ $$$$\mathrm{S}_{\mathrm{ABCD}} =\mathrm{S}_{\mathrm{ABC}} +\mathrm{S}_{\mathrm{ADC}} =\frac{\mathrm{1}}{\mathrm{2}}×\mathrm{2}×\mathrm{2}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{\mathrm{3}}×\mathrm{1}=\frac{\mathrm{3}}{\mathrm{2}}\sqrt{\mathrm{3}} \\ $$
Commented by Tinkutara last updated on 15/Jul/17

$$\mathrm{Thanks}\:\mathrm{Sir}! \\ $$
Commented by ajfour last updated on 14/Jul/17

$$\mathrm{S}_{\mathrm{ADC}} =\frac{\mathrm{1}}{\mathrm{2}}\mathrm{AD}×\mathrm{CD}=\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{\mathrm{3}}×\mathrm{1} \\ $$$$\mathrm{so}\:\:\mathrm{S}_{\mathrm{ABCD}} =\frac{\mathrm{3}\sqrt{\mathrm{3}}}{\mathrm{2}}\:\:. \\ $$$$\mathrm{thanks}\:\mathrm{sir},\:\mathrm{little}\:\mathrm{error}\:\mathrm{of}\:\mathrm{yours}\:\mathrm{is} \\ $$$$\mathrm{due}\:\mathrm{to}\:\mathrm{diagram},\:\mathrm{my}\:\mathrm{mistake};\:\angle\mathrm{ADC} \\ $$$$\mathrm{dont}\:\mathrm{appear}\:\mathrm{90}°\:\mathrm{in}\:\mathrm{the}\:\mathrm{diagram}. \\ $$
Commented by mrW1 last updated on 14/Jul/17
$$\mathrm{you}\:\mathrm{are}\:\mathrm{right}\:\mathrm{sir}. \\ $$$$\mathrm{i}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake}. \\ $$
Commented by Tinkutara last updated on 14/Jul/17
$$\mathrm{Is}\:\angle{ADC}\:=\:\mathrm{90}°\:\mathrm{is}\:\mathrm{to}\:\mathrm{be}\:\mathrm{given}\:\mathrm{or}\:\mathrm{to}\:\mathrm{be} \\ $$$$\mathrm{calculated}? \\ $$
Commented by mrW1 last updated on 14/Jul/17
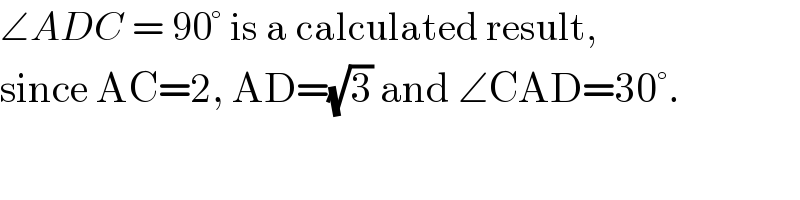
$$\angle{ADC}\:=\:\mathrm{90}°\:\mathrm{is}\:\mathrm{a}\:\mathrm{calculated}\:\mathrm{result}, \\ $$$$\mathrm{since}\:\mathrm{AC}=\mathrm{2},\:\mathrm{AD}=\sqrt{\mathrm{3}}\:\mathrm{and}\:\angle\mathrm{CAD}=\mathrm{30}°. \\ $$
