Menu Close

Question-180043

Tinku Tara 0 Comments
Pin




Question Number 180043 by mr W last updated on 06/Nov/22
Commented by CElcedricjunior last updated on 06/Nov/22
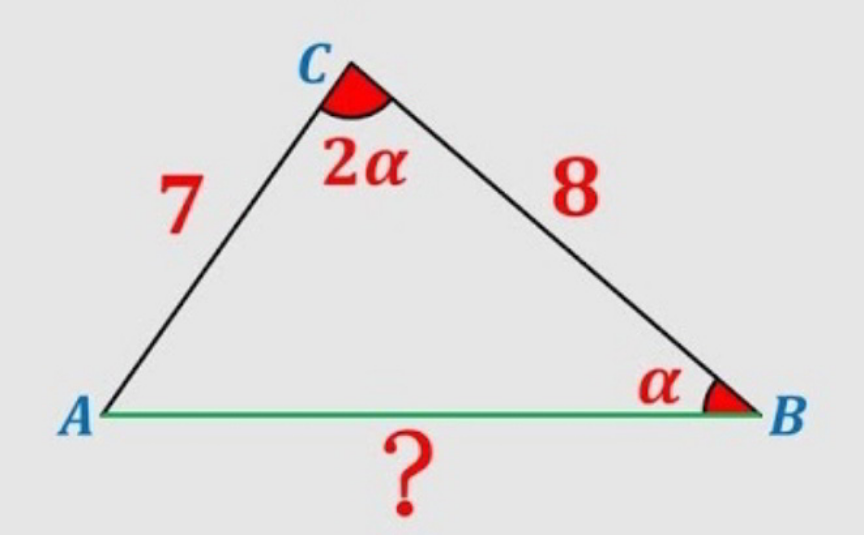
d′apres le theoreme des sinus (7/(sin𝛂))=(?/(sin2𝛂))=(8/(sin(𝛑−3𝛂))) =>(7/(sin𝛂))=(?/(sin2𝛂))=(8/(sin3𝛂)) ⇔(?/7)=2cos𝛂=>?=14cos𝛂=>?^2 =14^2 cos^2 𝛂 d′apres alkachy 7^2 +8^2 =?^2 +2×7×8cos2𝛂 =>?^2 =49+64−112cos2𝛂 ⇔14^2 cos𝛂=113−112cos2𝛂 ⇔196cos𝛂+112(1−2cos^2 𝛂)=113 ⇔224cos^2 𝛂−196cos𝛂+1=0 𝚫=196^2 −4×224=196^2 −896=37520 cos𝛂=((196−193.7)/(456))=((2.3)/(456))=>𝛂=arccos(((2.3)/(456)))=89.71 cos𝛂=((196+193.7)/(456))=((389.7)/(456))=𝛂=arccos(((389.7)/(456)))=31.28 d′ou^� 𝛂=31.28 cas2 𝛂∈]0;90[=>𝛂∈]0;45[ donc: ?=14cos𝛂=((14×389.7)/(456))=11.96
$$\boldsymbol{{d}}'\boldsymbol{{apres}}\:\boldsymbol{{le}}\:\boldsymbol{{theoreme}}\:\boldsymbol{{des}}\:\boldsymbol{{sinus}} \\ $$$$\frac{\mathrm{7}}{\boldsymbol{{sin}\alpha}}=\frac{?}{\boldsymbol{{sin}}\mathrm{2}\boldsymbol{\alpha}}=\frac{\mathrm{8}}{\boldsymbol{{sin}}\left(\boldsymbol{\pi}−\mathrm{3}\boldsymbol{\alpha}\right)} \\ $$$$=>\frac{\mathrm{7}}{\boldsymbol{{sin}\alpha}}=\frac{?}{\boldsymbol{{sin}}\mathrm{2}\boldsymbol{\alpha}}=\frac{\mathrm{8}}{\boldsymbol{{sin}}\mathrm{3}\boldsymbol{\alpha}} \\ $$$$\Leftrightarrow\frac{?}{\mathrm{7}}=\mathrm{2}\boldsymbol{{cos}\alpha}=>?=\mathrm{14}\boldsymbol{{cos}\alpha}=>?^{\mathrm{2}} =\mathrm{14}^{\mathrm{2}} \boldsymbol{{cos}}^{\mathrm{2}} \boldsymbol{\alpha} \\ $$$$\boldsymbol{{d}}'\boldsymbol{{apres}}\:\boldsymbol{{alkachy}} \\ $$$$\mathrm{7}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} =?^{\mathrm{2}} +\mathrm{2}×\mathrm{7}×\mathrm{8}\boldsymbol{{cos}}\mathrm{2}\boldsymbol{\alpha} \\ $$$$=>?^{\mathrm{2}} =\mathrm{49}+\mathrm{64}−\mathrm{112}\boldsymbol{{cos}}\mathrm{2}\boldsymbol{\alpha} \\ $$$$\Leftrightarrow\mathrm{14}^{\mathrm{2}} \boldsymbol{{cos}\alpha}=\mathrm{113}−\mathrm{112}\boldsymbol{{cos}}\mathrm{2}\boldsymbol{\alpha} \\ $$$$\Leftrightarrow\mathrm{196}\boldsymbol{{cos}\alpha}+\mathrm{112}\left(\mathrm{1}−\mathrm{2}\boldsymbol{{co}}\overset{\mathrm{2}} {\boldsymbol{{s}}\alpha}\right)=\mathrm{113} \\ $$$$\Leftrightarrow\mathrm{224}\boldsymbol{{co}}\overset{\mathrm{2}} {\boldsymbol{{s}}\alpha}−\mathrm{196}\boldsymbol{{cos}\alpha}+\mathrm{1}=\mathrm{0} \\ $$$$\boldsymbol{\Delta}=\mathrm{196}^{\mathrm{2}} −\mathrm{4}×\mathrm{224}=\mathrm{196}^{\mathrm{2}} −\mathrm{896}=\mathrm{37520} \\ $$$$\boldsymbol{{cos}\alpha}=\frac{\mathrm{196}−\mathrm{193}.\mathrm{7}}{\mathrm{456}}=\frac{\mathrm{2}.\mathrm{3}}{\mathrm{456}}=>\boldsymbol{\alpha}=\boldsymbol{{arccos}}\left(\frac{\mathrm{2}.\mathrm{3}}{\mathrm{456}}\right)=\mathrm{89}.\mathrm{71} \\ $$$$\boldsymbol{{cos}\alpha}=\frac{\mathrm{196}+\mathrm{193}.\mathrm{7}}{\mathrm{456}}=\frac{\mathrm{389}.\mathrm{7}}{\mathrm{456}}=\boldsymbol{\alpha}=\boldsymbol{{arccos}}\left(\frac{\mathrm{389}.\mathrm{7}}{\mathrm{456}}\right)=\mathrm{31}.\mathrm{28} \\ $$$$\left.\boldsymbol{{d}}'\boldsymbol{{o}}\grave {\boldsymbol{{u}}}\:\boldsymbol{\alpha}=\mathrm{31}.\mathrm{28}\:\boldsymbol{{cas}}\mathrm{2}\:\boldsymbol{\alpha}\in\right]\mathrm{0};\mathrm{90}\left[=>\boldsymbol{\alpha}\in\right]\mathrm{0};\mathrm{45}\left[\right. \\ $$$$\boldsymbol{{donc}}: \\ $$$$?=\mathrm{14}\boldsymbol{{cos}\alpha}=\frac{\mathrm{14}×\mathrm{389}.\mathrm{7}}{\mathrm{456}}=\mathrm{11}.\mathrm{96}\: \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by mr W last updated on 06/Nov/22
thanks for solving! but please don′t answer a question as comment!
$${thanks}\:{for}\:{solving}! \\ $$$${but}\:{please}\:{don}'{t}\:{answer}\:{a}\:{question}\:{as} \\ $$$${comment}! \\ $$
Commented by Acem last updated on 06/Nov/22
Q.179908
$${Q}.\mathrm{179908} \\ $$
Answered by srikanth2684 last updated on 06/Nov/22
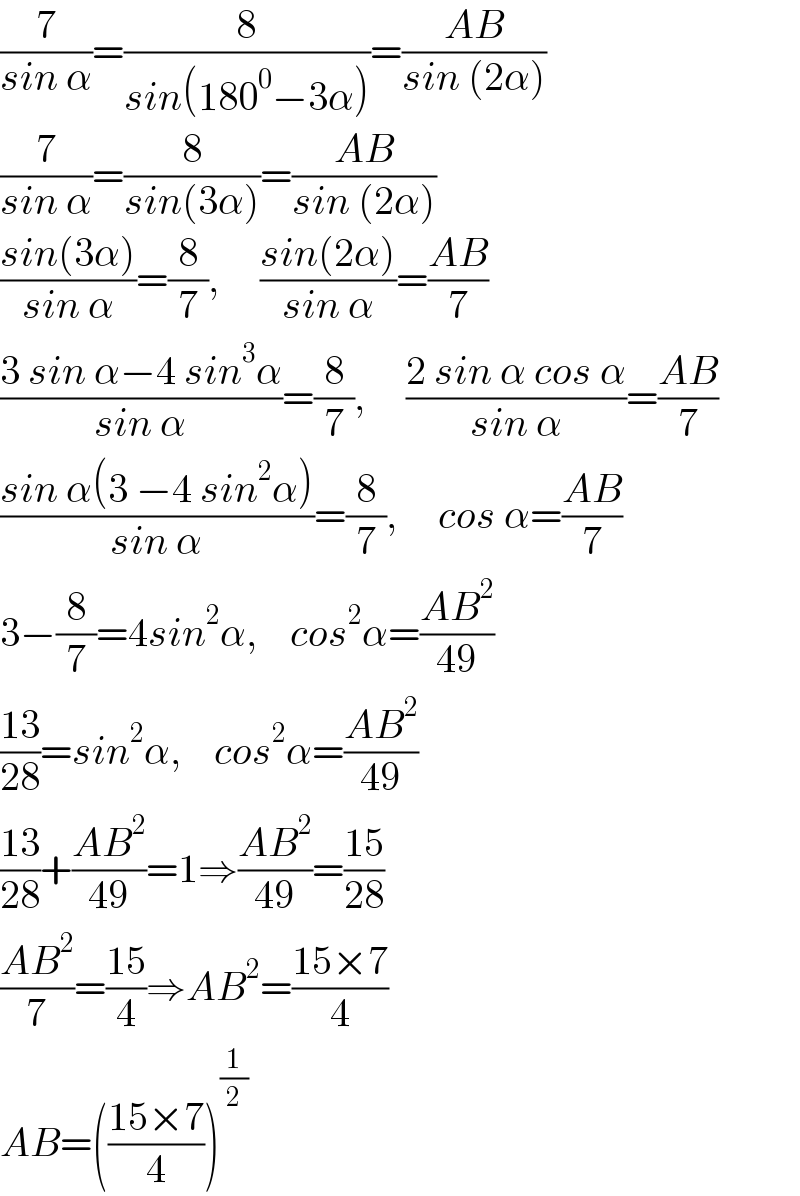
(7/(sin α))=(8/(sin(180^0 −3α)))=((AB)/(sin (2α))) (7/(sin α))=(8/(sin(3α)))=((AB)/(sin (2α))) ((sin(3α))/(sin α))=(8/7), ((sin(2α))/(sin α))=((AB)/7) ((3 sin α−4 sin^3 α)/(sin α))=(8/7), ((2 sin α cos α)/(sin α))=((AB)/7) ((sin α(3 −4 sin^2 α))/(sin α))=(8/7), cos α=((AB)/7) 3−(8/7)=4sin^2 α, cos^2 α=((AB^2 )/(49)) ((13)/(28))=sin^2 α, cos^2 α=((AB^2 )/(49)) ((13)/(28))+((AB^2 )/(49))=1⇒((AB^2 )/(49))=((15)/(28)) ((AB^2 )/7)=((15)/4)⇒AB^2 =((15×7)/4) AB=(((15×7)/4))^(1/2)
$$\frac{\mathrm{7}}{{sin}\:\alpha}=\frac{\mathrm{8}}{{sin}\left(\mathrm{180}^{\mathrm{0}} −\mathrm{3}\alpha\right)}=\frac{{AB}}{{sin}\:\left(\mathrm{2}\alpha\right)} \\ $$$$\frac{\mathrm{7}}{{sin}\:\alpha}=\frac{\mathrm{8}}{{sin}\left(\mathrm{3}\alpha\right)}=\frac{{AB}}{{sin}\:\left(\mathrm{2}\alpha\right)} \\ $$$$\frac{{sin}\left(\mathrm{3}\alpha\right)}{{sin}\:\alpha}=\frac{\mathrm{8}}{\mathrm{7}},\:\:\:\:\:\frac{{sin}\left(\mathrm{2}\alpha\right)}{{sin}\:\alpha}=\frac{{AB}}{\mathrm{7}} \\ $$$$\frac{\mathrm{3}\:{sin}\:\alpha−\mathrm{4}\:{sin}^{\mathrm{3}} \alpha}{{sin}\:\alpha}=\frac{\mathrm{8}}{\mathrm{7}},\:\:\:\:\:\frac{\mathrm{2}\:{sin}\:\alpha\:{cos}\:\alpha}{{sin}\:\alpha}=\frac{{AB}}{\mathrm{7}} \\ $$$$\frac{{sin}\:\alpha\left(\mathrm{3}\:−\mathrm{4}\:{sin}^{\mathrm{2}} \alpha\right)}{{sin}\:\alpha}=\frac{\mathrm{8}}{\mathrm{7}},\:\:\:\:\:{cos}\:\alpha=\frac{{AB}}{\mathrm{7}} \\ $$$$\mathrm{3}−\frac{\mathrm{8}}{\mathrm{7}}=\mathrm{4}{sin}^{\mathrm{2}} \alpha,\:\:\:\:{cos}^{\mathrm{2}} \alpha=\frac{{AB}^{\mathrm{2}} }{\mathrm{49}} \\ $$$$\frac{\mathrm{13}}{\mathrm{28}}={sin}^{\mathrm{2}} \alpha,\:\:\:\:{cos}^{\mathrm{2}} \alpha=\frac{{AB}^{\mathrm{2}} }{\mathrm{49}} \\ $$$$\frac{\mathrm{13}}{\mathrm{28}}+\frac{{AB}^{\mathrm{2}} }{\mathrm{49}}=\mathrm{1}\Rightarrow\frac{{AB}^{\mathrm{2}} }{\mathrm{49}}=\frac{\mathrm{15}}{\mathrm{28}} \\ $$$$\frac{{AB}^{\mathrm{2}} }{\mathrm{7}}=\frac{\mathrm{15}}{\mathrm{4}}\Rightarrow{AB}^{\mathrm{2}} =\frac{\mathrm{15}×\mathrm{7}}{\mathrm{4}} \\ $$$${AB}=\left(\frac{\mathrm{15}×\mathrm{7}}{\mathrm{4}}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$
Answered by Frix last updated on 06/Nov/22
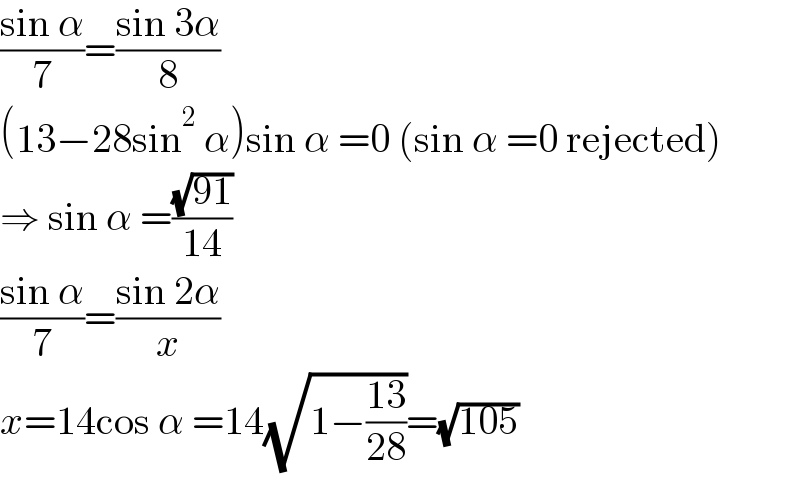
((sin α)/7)=((sin 3α)/8) (13−28sin^2 α)sin α =0 (sin α =0 rejected) ⇒ sin α =((√(91))/(14)) ((sin α)/7)=((sin 2α)/x) x=14cos α =14(√(1−((13)/(28))))=(√(105))
$$\frac{\mathrm{sin}\:\alpha}{\mathrm{7}}=\frac{\mathrm{sin}\:\mathrm{3}\alpha}{\mathrm{8}} \\ $$$$\left(\mathrm{13}−\mathrm{28sin}^{\mathrm{2}} \:\alpha\right)\mathrm{sin}\:\alpha\:=\mathrm{0}\:\left(\mathrm{sin}\:\alpha\:=\mathrm{0}\:\mathrm{rejected}\right) \\ $$$$\Rightarrow\:\mathrm{sin}\:\alpha\:=\frac{\sqrt{\mathrm{91}}}{\mathrm{14}} \\ $$$$\frac{\mathrm{sin}\:\alpha}{\mathrm{7}}=\frac{\mathrm{sin}\:\mathrm{2}\alpha}{{x}} \\ $$$${x}=\mathrm{14cos}\:\alpha\:=\mathrm{14}\sqrt{\mathrm{1}−\frac{\mathrm{13}}{\mathrm{28}}}=\sqrt{\mathrm{105}} \\ $$
Commented by mr W last updated on 06/Nov/22
thanks sir!
$${thanks}\:{sir}! \\ $$
Answered by mr W last updated on 06/Nov/22
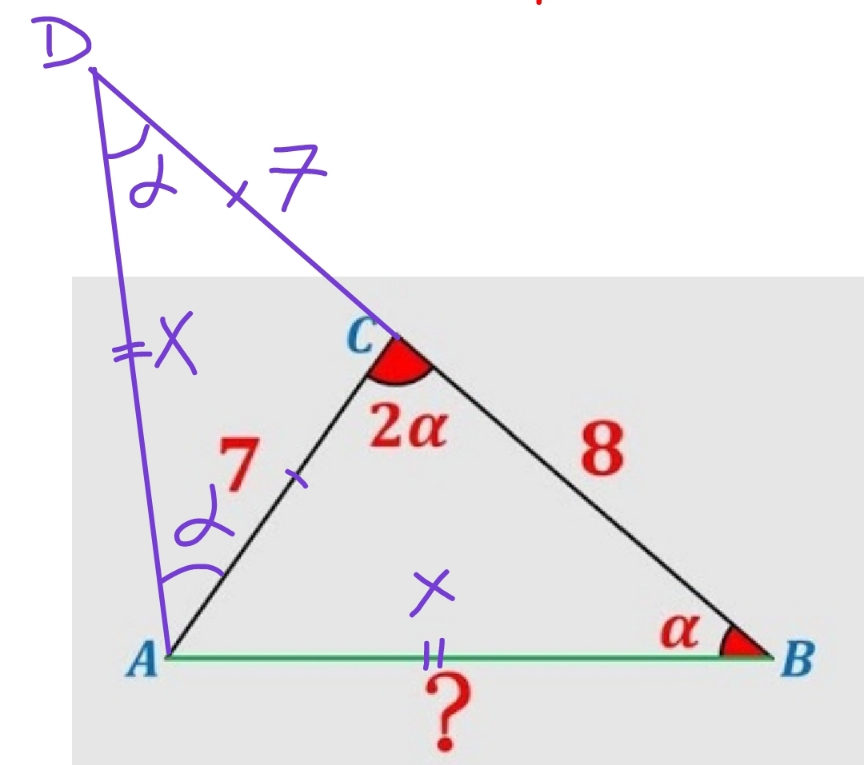
Commented by mr W last updated on 06/Nov/22
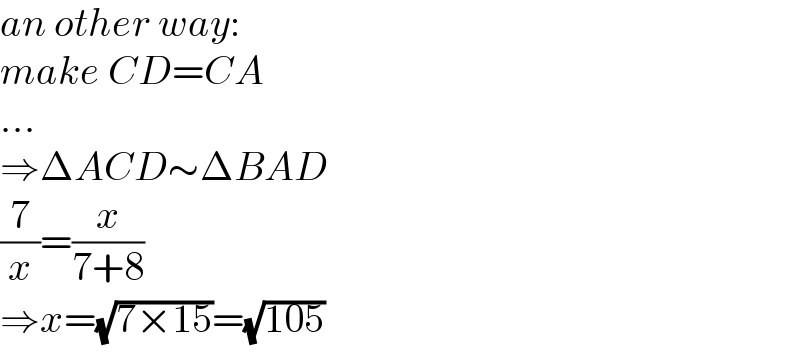
an other way: make CD=CA ... ⇒ΔACD∼ΔBAD (7/x)=(x/(7+8)) ⇒x=(√(7×15))=(√(105))
$${an}\:{other}\:{way}: \\ $$$${make}\:{CD}={CA} \\ $$$$… \\ $$$$\Rightarrow\Delta{ACD}\sim\Delta{BAD} \\ $$$$\frac{\mathrm{7}}{{x}}=\frac{{x}}{\mathrm{7}+\mathrm{8}} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{7}×\mathrm{15}}=\sqrt{\mathrm{105}} \\ $$
Answered by a.lgnaoui last updated on 06/Nov/22
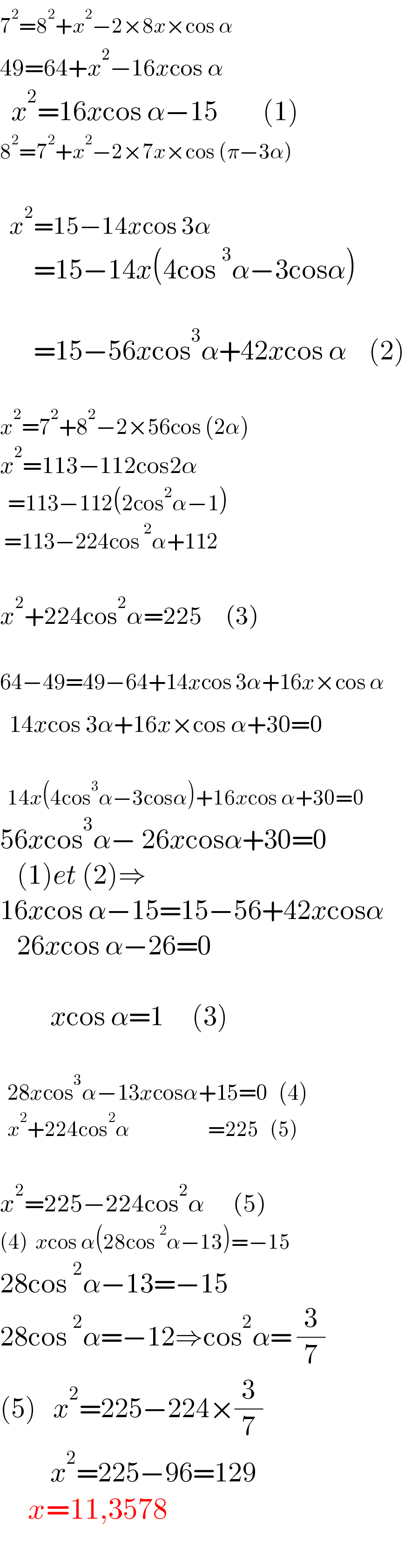
7^2 =8^2 +x^2 −2×8x×cos α^ 49=64+x^2 −16xcos α ^ x^2 =16xcos α−15 (1) 8^2 =7^2 +x^2 −2×7x×cos (π−3α) x^2 =15−14xcos 3α =15−14x(4cos^3 α−3cosα) =15−56xcos^3 α+42xcos α (2) x^2 =7^2 +8^2 −2×56cos (2α) x^2 =113−112cos2α =113−112(2cos^2 α−1) =113−224cos^2 α+112 x^2 +224cos^2 α=225 (3) 64−49=49−64+14xcos 3α+16x×cos α 14xcos 3α+16x×cos α+30=0^ 14x(4cos^3 α−3cosα)+16xcos α+30=0 56xcos^3 α− 26xcosα+30=0 (1)et (2)⇒ 16xcos α−15=15−56+42xcosα 26xcos α−26=0 xcos α=1 (3) 28xcos^3 α−13xcosα+15=0 (4) x^2 +224cos^2 α =225 (5) x^2 =225−224cos^2 α (5) (4) xcos α(28cos^2 α−13)=−15 28cos^2 α−13=−15 28cos^2 α=−12⇒cos^2 α= (3/7) (5) x^2 =225−224×(3/7) x^2 =225−96=129 x=11,3578
$$\mathrm{7}^{\mathrm{2}} =\mathrm{8}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}×\mathrm{8}{x}×\mathrm{cos}\:\overset{} {\alpha} \\ $$$$\mathrm{49}=\mathrm{64}+{x}^{\mathrm{2}} −\mathrm{16}{x}\mathrm{cos}\:\alpha\:\:\overset{} {\:}\:\:\:\: \\ $$$$\:\:{x}^{\mathrm{2}} =\mathrm{16}{x}\mathrm{cos}\:\alpha−\mathrm{15}\:\:\:\:\:\:\:\:\left(\mathrm{1}\right) \\ $$$$\mathrm{8}^{\mathrm{2}} =\mathrm{7}^{\mathrm{2}} +{x}^{\mathrm{2}} −\mathrm{2}×\mathrm{7}{x}×\mathrm{cos}\:\left(\pi−\mathrm{3}\alpha\right) \\ $$$$ \\ $$$$\:\:{x}^{\mathrm{2}} =\mathrm{15}−\mathrm{14}{x}\mathrm{cos}\:\mathrm{3}\alpha \\ $$$$\:\:\:\:\:\:=\mathrm{15}−\mathrm{14}{x}\left(\mathrm{4cos}\:^{\mathrm{3}} \alpha−\mathrm{3cos}\alpha\right)\: \\ $$$$ \\ $$$$\:\:\:\:\:\:=\mathrm{15}−\mathrm{56}{x}\mathrm{cos}^{\mathrm{3}} \alpha+\mathrm{42}{x}\mathrm{cos}\:\alpha\:\:\:\:\left(\mathrm{2}\right) \\ $$$$ \\ $$$${x}^{\mathrm{2}} =\mathrm{7}^{\mathrm{2}} +\mathrm{8}^{\mathrm{2}} −\mathrm{2}×\mathrm{56cos}\:\left(\mathrm{2}\alpha\right) \\ $$$${x}^{\mathrm{2}} =\mathrm{113}−\mathrm{112cos2}\alpha \\ $$$$\:\:=\mathrm{113}−\mathrm{112}\left(\mathrm{2cos}^{\mathrm{2}} \alpha−\mathrm{1}\right) \\ $$$$\:=\mathrm{113}−\mathrm{224cos}\:^{\mathrm{2}} \alpha+\mathrm{112} \\ $$$$ \\ $$$${x}^{\mathrm{2}} +\mathrm{224cos}^{\mathrm{2}} \alpha=\mathrm{225}\:\:\:\:\:\left(\mathrm{3}\right) \\ $$$$\:\: \\ $$$$\mathrm{64}−\mathrm{49}=\mathrm{49}−\mathrm{64}+\mathrm{14}{x}\mathrm{cos}\:\mathrm{3}\alpha+\mathrm{16}{x}×\mathrm{cos}\:\alpha \\ $$$$\:\:\mathrm{14}{x}\mathrm{cos}\:\mathrm{3}\alpha+\mathrm{16}{x}×\mathrm{cos}\:\alpha+\mathrm{30}=\overset{} {\mathrm{0}} \\ $$$$\:\: \\ $$$$\:\:\mathrm{14}{x}\left(\mathrm{4cos}^{\mathrm{3}} \alpha−\mathrm{3cos}\alpha\right)+\mathrm{16}{x}\mathrm{cos}\:\alpha+\mathrm{30}=\mathrm{0} \\ $$$$\mathrm{56}{x}\mathrm{cos}^{\mathrm{3}} \alpha−\:\mathrm{26}{x}\mathrm{cos}\alpha+\mathrm{30}=\mathrm{0}\: \\ $$$$\:\:\:\left(\mathrm{1}\right){et}\:\left(\mathrm{2}\right)\Rightarrow \\ $$$$\mathrm{16}{x}\mathrm{cos}\:\alpha−\mathrm{15}=\mathrm{15}−\mathrm{56}+\mathrm{42}{x}\mathrm{cos}\alpha \\ $$$$\:\:\:\mathrm{26}{x}\mathrm{cos}\:\alpha−\mathrm{26}=\mathrm{0} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:{x}\mathrm{cos}\:\alpha=\mathrm{1}\:\:\:\:\:\left(\mathrm{3}\right) \\ $$$$ \\ $$$$\:\:\mathrm{28}{x}\mathrm{cos}^{\mathrm{3}} \alpha−\mathrm{13}{x}\mathrm{cos}\alpha+\mathrm{15}=\mathrm{0}\:\:\:\left(\mathrm{4}\right)\:\: \\ $$$$\:\:{x}^{\mathrm{2}} +\mathrm{224cos}^{\mathrm{2}} \alpha\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{225}\:\:\:\left(\mathrm{5}\right) \\ $$$$ \\ $$$${x}^{\mathrm{2}} =\mathrm{225}−\mathrm{224cos}^{\mathrm{2}} \alpha\:\:\:\:\:\:\left(\mathrm{5}\right) \\ $$$$\left(\mathrm{4}\right)\:\:{x}\mathrm{cos}\:\alpha\left(\mathrm{28cos}\:^{\mathrm{2}} \alpha−\mathrm{13}\right)=−\mathrm{15} \\ $$$$\mathrm{28cos}\:^{\mathrm{2}} \alpha−\mathrm{13}=−\mathrm{15} \\ $$$$\mathrm{28cos}\:^{\mathrm{2}} \alpha=−\mathrm{12}\Rightarrow\mathrm{cos}^{\mathrm{2}} \alpha=\:\frac{\mathrm{3}}{\mathrm{7}} \\ $$$$\left(\mathrm{5}\right)\:\:\:{x}^{\mathrm{2}} =\mathrm{225}−\mathrm{224}×\frac{\mathrm{3}}{\mathrm{7}} \\ $$$$\:\:\:\:\:\:\:\:\:{x}^{\mathrm{2}} =\mathrm{225}−\mathrm{96}=\mathrm{129} \\ $$$$\:\:\:\:\:{x}=\mathrm{11},\mathrm{3578} \\ $$$$ \\ $$
Commented by mr W last updated on 07/Nov/22
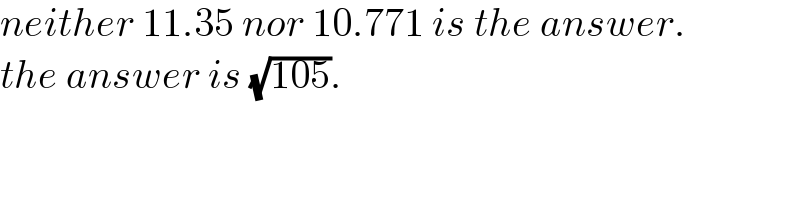
neither 11.35 nor 10.771 is the answer. the answer is (√(105)).
$${neither}\:\mathrm{11}.\mathrm{35}\:{nor}\:\mathrm{10}.\mathrm{771}\:{is}\:{the}\:{answer}. \\ $$$${the}\:{answer}\:{is}\:\sqrt{\mathrm{105}}. \\ $$
Commented by a.lgnaoui last updated on 06/Nov/22
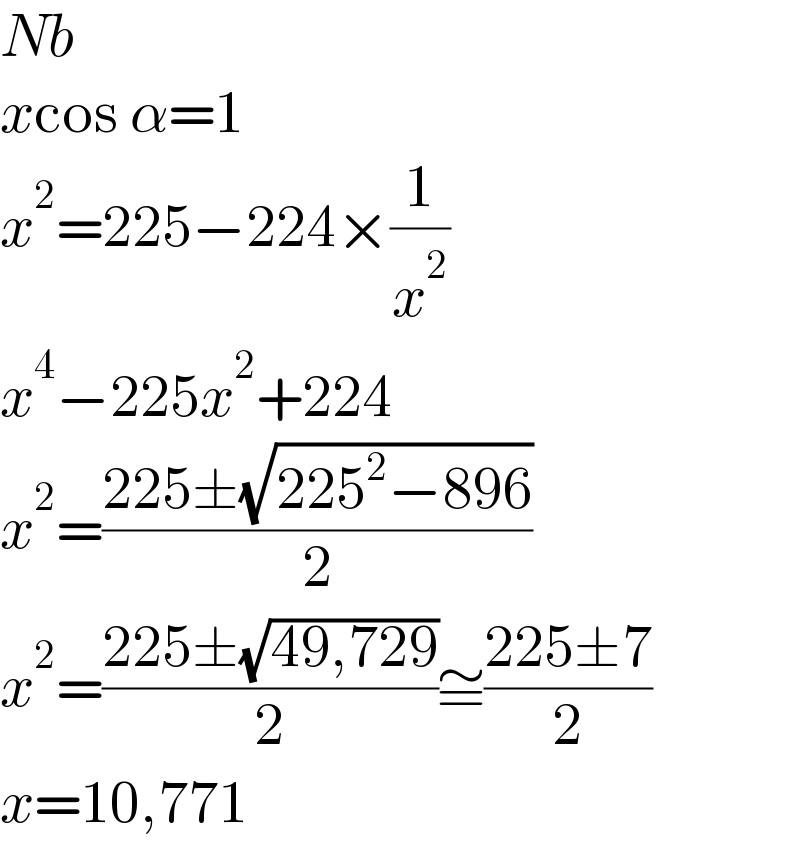
Nb xcos α=1 x^2 =225−224×(1/x^2 ) x^4 −225x^2 +224 x^2 =((225±(√(225^2 −896)))/2) x^2 =((225±(√(49,729)))/2)≅((225±7)/2) x=10,771
$${Nb} \\ $$$${x}\mathrm{cos}\:\alpha=\mathrm{1}\:\:\:\: \\ $$$${x}^{\mathrm{2}} =\mathrm{225}−\mathrm{224}×\frac{\mathrm{1}}{{x}^{\mathrm{2}} } \\ $$$${x}^{\mathrm{4}} −\mathrm{225}{x}^{\mathrm{2}} +\mathrm{224} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{225}\pm\sqrt{\mathrm{225}^{\mathrm{2}} −\mathrm{896}}}{\mathrm{2}} \\ $$$${x}^{\mathrm{2}} =\frac{\mathrm{225}\pm\sqrt{\mathrm{49},\mathrm{729}}}{\mathrm{2}}\cong\frac{\mathrm{225}\pm\mathrm{7}}{\mathrm{2}} \\ $$$${x}=\mathrm{10},\mathrm{771} \\ $$
Commented by a.lgnaoui last updated on 06/Nov/22
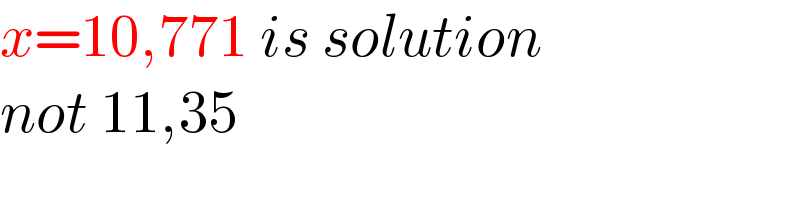
x=10,771 is solution not 11,35
$${x}=\mathrm{10},\mathrm{771}\:{is}\:{solution} \\ $$$${not}\:\mathrm{11},\mathrm{35} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *