Menu Close

Question-180104

Tinku Tara 0 Comments
Pin




Question Number 180104 by mr W last updated on 07/Nov/22
Commented by mr W last updated on 07/Nov/22
A lies on x−axis and B on the curve y=x^2 . P is at (4,4). find the smallest perimeter of triangle PAB.
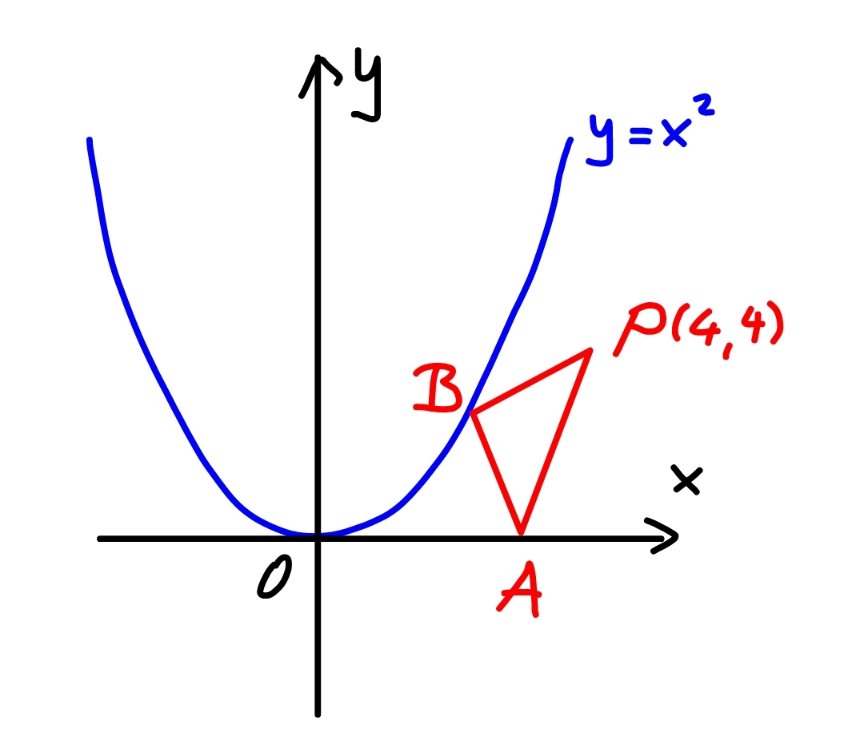
$${A}\:{lies}\:{on}\:{x}−{axis}\:{and}\:{B}\:{on}\:{the}\:{curve} \\ $$$${y}={x}^{\mathrm{2}} .\:{P}\:{is}\:{at}\:\left(\mathrm{4},\mathrm{4}\right).\:{find}\:{the}\:{smallest} \\ $$$${perimeter}\:{of}\:{triangle}\:{PAB}. \\ $$
Answered by mr W last updated on 07/Nov/22
Commented by mr W last updated on 07/Nov/22
say B(t,t^2 ) tangent at B: y−t^2 =2t(x−t) 2tx−y−t^2 =0 P_1 (4,−4) P_2 (x_2 ,y_2 ) = image of P in tangent x_2 =4−((4t(8t−4−t^2 ))/(4t^2 +1)) y_2 =4+((2(8t−4−t^2 ))/(4t^2 +1)) P_2 , B and P_1 should be collinear, ((x_2 −t)/(t−4))=((y_2 −t^2 )/(t^2 +4)) (((4−t)(4t^2 +1)−4t(8t−4−t^2 ))/(t−4))=(((4−t^2 )(4t^2 +1)+2(8t−4−t^2 ))/(t^2 +4)) 2t^4 −16t^3 +t^2 −12t+64=0 ⇒t≈1.5475 P=(√((t−4)^2 +(t^2 −4)^2 ))+(√((t−4)^2 +(t^2 +4)^2 )) P_(min) ≈9.7801
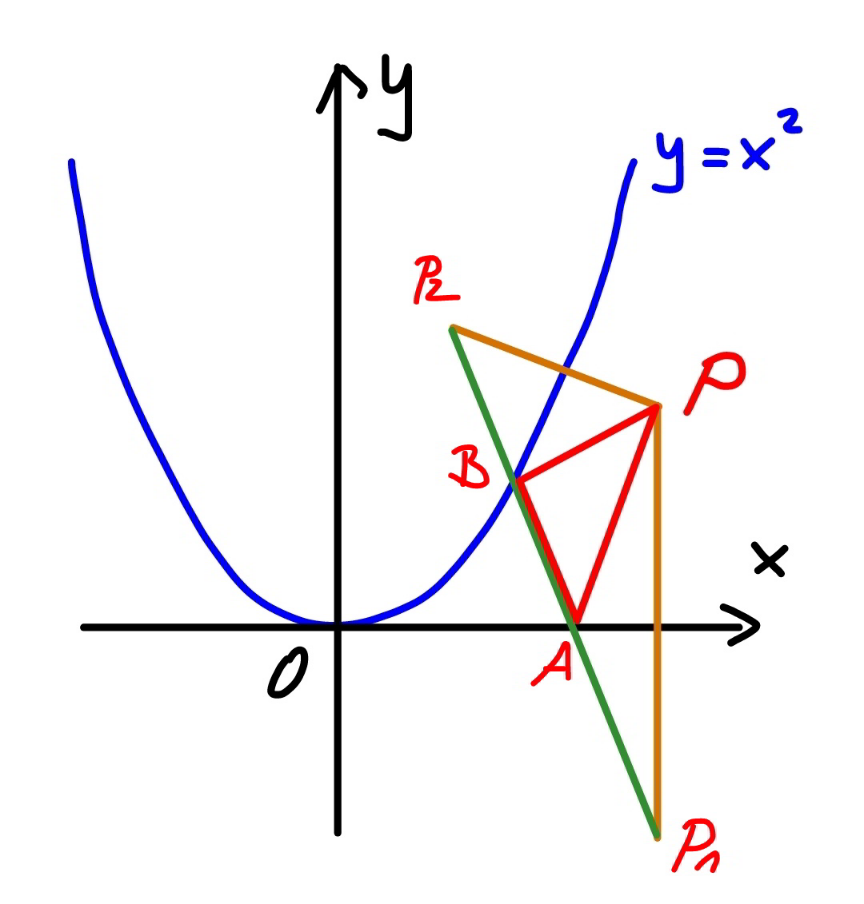
$${say}\:{B}\left({t},{t}^{\mathrm{2}} \right) \\ $$$${tangent}\:{at}\:{B}: \\ $$$${y}−{t}^{\mathrm{2}} =\mathrm{2}{t}\left({x}−{t}\right) \\ $$$$\mathrm{2}{tx}−{y}−{t}^{\mathrm{2}} =\mathrm{0} \\ $$$$ \\ $$$${P}_{\mathrm{1}} \left(\mathrm{4},−\mathrm{4}\right) \\ $$$${P}_{\mathrm{2}} \left({x}_{\mathrm{2}} ,{y}_{\mathrm{2}} \right)\:=\:{image}\:{of}\:{P}\:{in}\:{tangent} \\ $$$${x}_{\mathrm{2}} =\mathrm{4}−\frac{\mathrm{4}{t}\left(\mathrm{8}{t}−\mathrm{4}−{t}^{\mathrm{2}} \right)}{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${y}_{\mathrm{2}} =\mathrm{4}+\frac{\mathrm{2}\left(\mathrm{8}{t}−\mathrm{4}−{t}^{\mathrm{2}} \right)}{\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${P}_{\mathrm{2}} ,\:{B}\:{and}\:{P}_{\mathrm{1}} \:{should}\:{be}\:{collinear}, \\ $$$$\frac{{x}_{\mathrm{2}} −{t}}{{t}−\mathrm{4}}=\frac{{y}_{\mathrm{2}} −{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} +\mathrm{4}} \\ $$$$\frac{\left(\mathrm{4}−{t}\right)\left(\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}\right)−\mathrm{4}{t}\left(\mathrm{8}{t}−\mathrm{4}−{t}^{\mathrm{2}} \right)}{{t}−\mathrm{4}}=\frac{\left(\mathrm{4}−{t}^{\mathrm{2}} \right)\left(\mathrm{4}{t}^{\mathrm{2}} +\mathrm{1}\right)+\mathrm{2}\left(\mathrm{8}{t}−\mathrm{4}−{t}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} +\mathrm{4}} \\ $$$$\mathrm{2}{t}^{\mathrm{4}} −\mathrm{16}{t}^{\mathrm{3}} +{t}^{\mathrm{2}} −\mathrm{12}{t}+\mathrm{64}=\mathrm{0} \\ $$$$\Rightarrow{t}\approx\mathrm{1}.\mathrm{5475} \\ $$$${P}=\sqrt{\left({t}−\mathrm{4}\right)^{\mathrm{2}} +\left({t}^{\mathrm{2}} −\mathrm{4}\right)^{\mathrm{2}} }+\sqrt{\left({t}−\mathrm{4}\right)^{\mathrm{2}} +\left({t}^{\mathrm{2}} +\mathrm{4}\right)^{\mathrm{2}} } \\ $$$${P}_{{min}} \approx\mathrm{9}.\mathrm{7801} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *