Question-180107

Question Number 180107 by yaslm last updated on 07/Nov/22

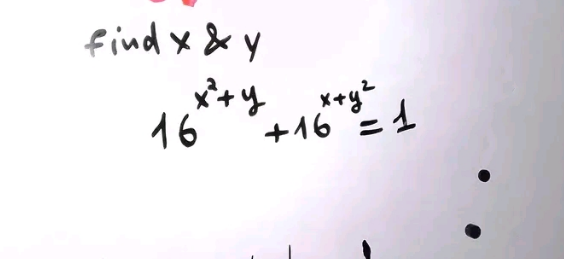
Commented by MJS_new last updated on 07/Nov/22

$$\mathrm{only}\:\mathrm{real}\:\mathrm{solution} \\ $$$${x}={y}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$

Commented by Rasheed.Sindhi last updated on 08/Nov/22

16^(x^2 +y) +16^(x+y^2 ) =1 16^(x+y) (16^x +16^y )=1 16^(x+y) =(1/(16^x +16^y )) ab=(1/(a+b)) ; [16^x =a,16^y =b] .... ...

$$\mathrm{16}^{{x}^{\mathrm{2}} +{y}} +\mathrm{16}^{{x}+{y}^{\mathrm{2}} } =\mathrm{1} \\ $$$$\mathrm{16}^{{x}+{y}} \left(\mathrm{16}^{{x}} +\mathrm{16}^{{y}} \right)=\mathrm{1} \\ $$$$\mathrm{16}^{{x}+{y}} =\frac{\mathrm{1}}{\mathrm{16}^{{x}} +\mathrm{16}^{{y}} } \\ $$$${ab}=\frac{\mathrm{1}}{{a}+{b}}\:\:;\:\left[\mathrm{16}^{{x}} ={a},\mathrm{16}^{{y}} ={b}\right] \\ $$$$…. \\ $$$$… \\ $$

Commented by MJS_new last updated on 08/Nov/22

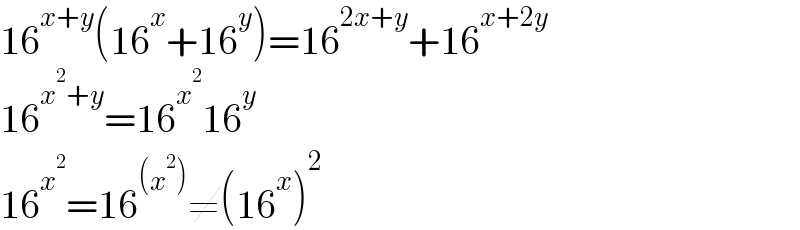
16^(x+y) (16^x +16^y )=16^(2x+y) +16^(x+2y) 16^(x^2 +y) =16^x^2 16^y 16^x^2 =16^((x^2 )) ≠(16^x )^2

$$\mathrm{16}^{{x}+{y}} \left(\mathrm{16}^{{x}} +\mathrm{16}^{{y}} \right)=\mathrm{16}^{\mathrm{2}{x}+{y}} +\mathrm{16}^{{x}+\mathrm{2}{y}} \\ $$$$\mathrm{16}^{{x}^{\mathrm{2}} +{y}} =\mathrm{16}^{{x}^{\mathrm{2}} } \mathrm{16}^{{y}} \\ $$$$\mathrm{16}^{{x}^{\mathrm{2}} } =\mathrm{16}^{\left({x}^{\mathrm{2}} \right)} \neq\left(\mathrm{16}^{{x}} \right)^{\mathrm{2}} \\ $$

Commented by Rasheed.Sindhi last updated on 08/Nov/22