Question Number 180258 by mr W last updated on 09/Nov/22

Commented by mr W last updated on 09/Nov/22
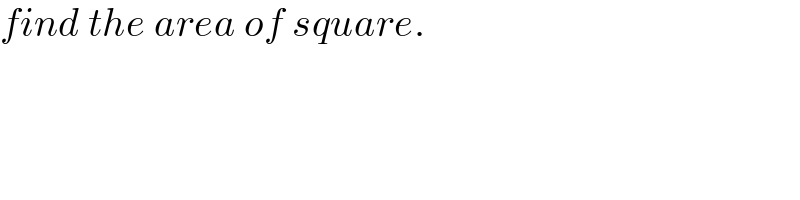
$${find}\:{the}\:{area}\:{of}\:{square}. \\ $$
Answered by HeferH last updated on 09/Nov/22
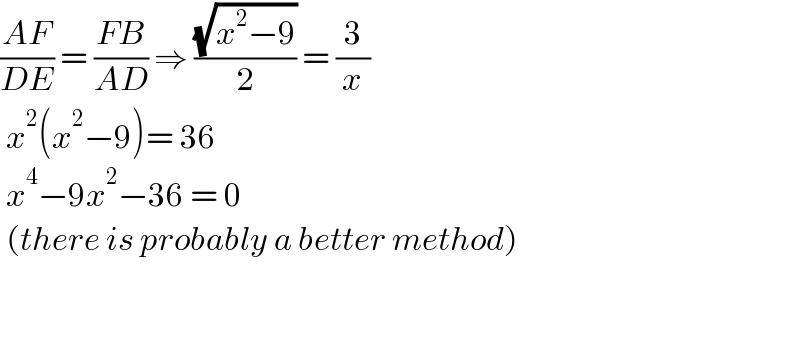
$$\frac{{AF}}{{DE}}\:=\:\frac{{FB}}{{AD}}\:\Rightarrow\:\frac{\sqrt{{x}^{\mathrm{2}} −\mathrm{9}}}{\mathrm{2}}\:=\:\frac{\mathrm{3}}{{x}} \\ $$$$\:{x}^{\mathrm{2}} \left({x}^{\mathrm{2}} −\mathrm{9}\right)=\:\mathrm{36} \\ $$$$\:{x}^{\mathrm{4}} −\mathrm{9}{x}^{\mathrm{2}} −\mathrm{36}\:=\:\mathrm{0} \\ $$$$\:\left({there}\:{is}\:{probably}\:{a}\:{better}\:{method}\right) \\ $$$$\: \\ $$$$\: \\ $$
Commented by mr W last updated on 10/Nov/22

$${thanks}! \\ $$
Answered by Acem last updated on 09/Nov/22
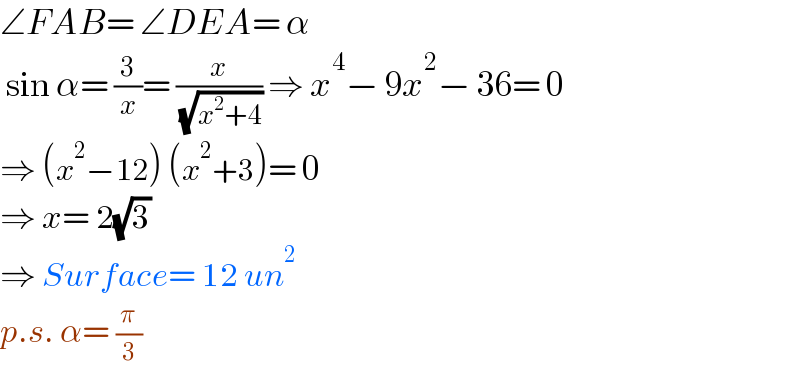
$$\angle{FAB}=\:\angle{DEA}=\:\alpha \\ $$$$\:\mathrm{sin}\:\alpha=\:\frac{\mathrm{3}}{{x}}=\:\frac{{x}}{\:\sqrt{{x}^{\mathrm{2}} +\mathrm{4}}}\:\Rightarrow\:{x}^{\mathrm{4}} −\:\mathrm{9}{x}^{\mathrm{2}} −\:\mathrm{36}=\:\mathrm{0} \\ $$$$\Rightarrow\:\left({x}^{\mathrm{2}} −\mathrm{12}\right)\:\left({x}^{\mathrm{2}} +\mathrm{3}\right)=\:\mathrm{0} \\ $$$$\Rightarrow\:{x}=\:\mathrm{2}\sqrt{\mathrm{3}}\: \\ $$$$\Rightarrow\:{Surface}=\:\mathrm{12}\:{un}^{\mathrm{2}} \\ $$$${p}.{s}.\:\alpha=\:\frac{\pi}{\mathrm{3}} \\ $$
Commented by mr W last updated on 10/Nov/22

$${thanks}! \\ $$
