Question Number 180268 by Noorzai last updated on 09/Nov/22
Answered by Ar Brandon last updated on 09/Nov/22

$$\mathrm{Q121680} \\ $$
Answered by LEKOUMA last updated on 10/Nov/22
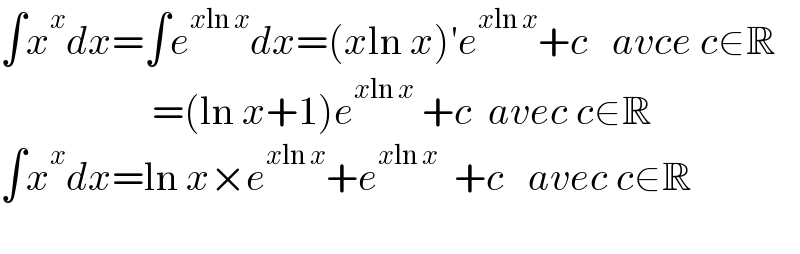
$$\int{x}^{{x}} {dx}=\int{e}^{{x}\mathrm{ln}\:{x}} {dx}=\left({x}\mathrm{ln}\:{x}\right)'{e}^{{x}\mathrm{ln}\:{x}} +{c}\:\:\:{avce}\:{c}\in\mathbb{R} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left(\mathrm{ln}\:{x}+\mathrm{1}\right){e}^{{x}\mathrm{ln}\:{x}} \:+{c}\:\:{avec}\:{c}\in\mathbb{R} \\ $$$$\int{x}^{{x}} {dx}=\mathrm{ln}\:{x}×{e}^{{x}\mathrm{ln}\:{x}} +{e}^{{x}\mathrm{ln}\:{x}} \:\:+{c}\:\:\:{avec}\:{c}\in\mathbb{R} \\ $$$$ \\ $$
Commented by mr W last updated on 10/Nov/22
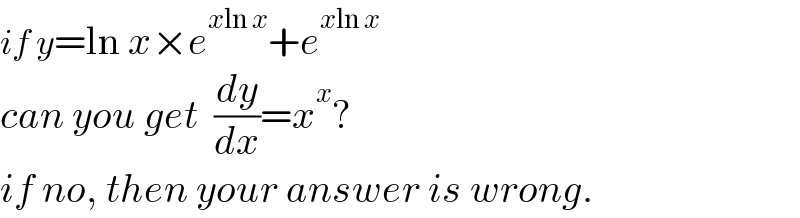
$${if}\:{y}=\mathrm{ln}\:{x}×{e}^{{x}\mathrm{ln}\:{x}} +{e}^{{x}\mathrm{ln}\:{x}} \\ $$$${can}\:{you}\:{get}\:\:\frac{{dy}}{{dx}}={x}^{{x}} ? \\ $$$${if}\:{no},\:{then}\:{your}\:{answer}\:{is}\:{wrong}. \\ $$
