Menu Close

Question-180300

Tinku Tara 0 Comments
Pin




Question Number 180300 by mnjuly1970 last updated on 10/Nov/22
Answered by Acem last updated on 11/Nov/22
Commented by Acem last updated on 11/Nov/22
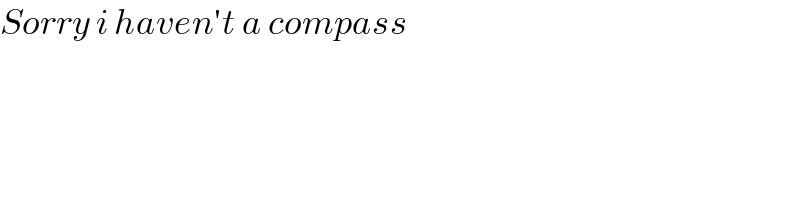
Sorry i haven′t a compass
$${Sorry}\:{i}\:{haven}'{t}\:{a}\:{compass} \\ $$
Commented by mr W last updated on 12/Nov/22
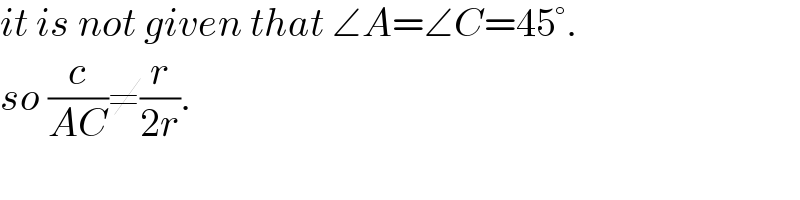
it is not given that ∠A=∠C=45°. so (c/(AC))≠(r/(2r)).
$${it}\:{is}\:{not}\:{given}\:{that}\:\angle{A}=\angle{C}=\mathrm{45}°. \\ $$$${so}\:\frac{{c}}{{AC}}\neq\frac{{r}}{\mathrm{2}{r}}. \\ $$
Commented by Acem last updated on 12/Nov/22
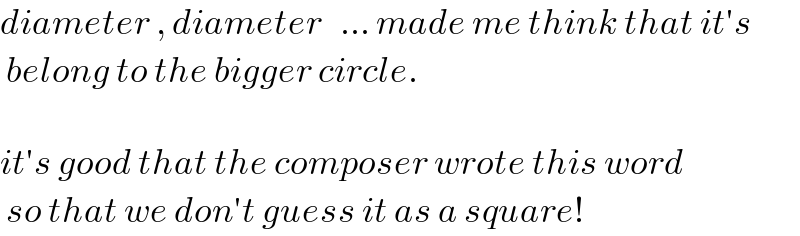
diameter , diameter ... made me think that it′s belong to the bigger circle. it′s good that the composer wrote this word so that we don′t guess it as a square!
$${diameter}\:,\:{diameter}\:\:\:…\:{made}\:{me}\:{think}\:{that}\:{it}'{s} \\ $$$$\:{belong}\:{to}\:{the}\:{bigger}\:{circle}. \\ $$$$ \\ $$$${it}'{s}\:{good}\:{that}\:{the}\:{composer}\:{wrote}\:{this}\:{word} \\ $$$$\:{so}\:{that}\:{we}\:{don}'{t}\:{guess}\:{it}\:{as}\:{a}\:{square}! \\ $$
Answered by a.lgnaoui last updated on 11/Nov/22
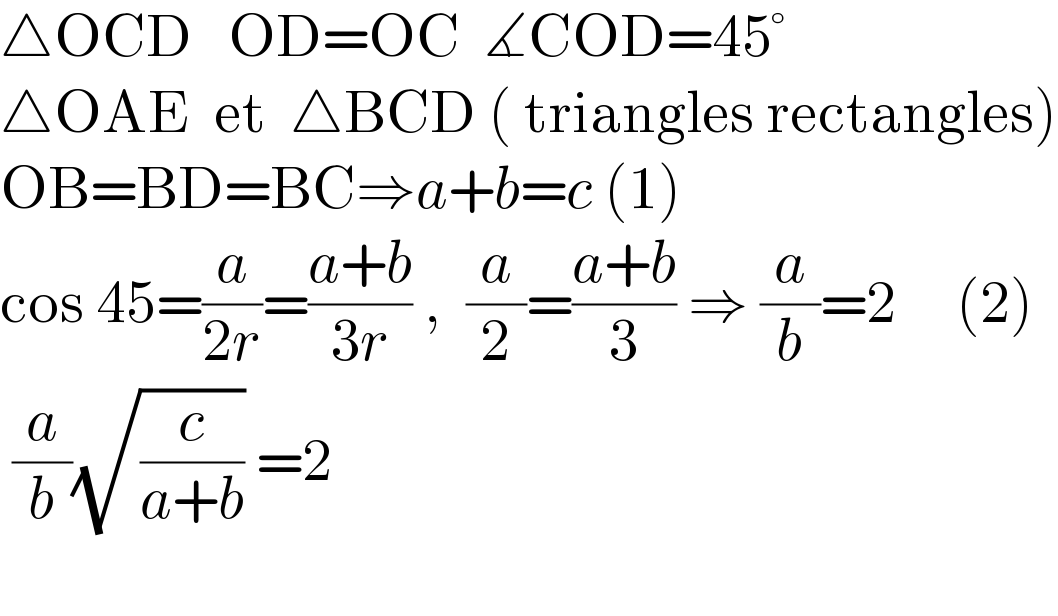
△OCD OD=OC ∡COD=45° △OAE et △BCD ( triangles rectangles) OB=BD=BC⇒a+b=c (1) cos 45=(a/(2r))=((a+b)/(3r)) , (a/2)=((a+b)/3) ⇒ (a/b)=2 (2) (a/b)(√(c/(a+b))) =2
$$\bigtriangleup\mathrm{OCD}\:\:\:\mathrm{OD}=\mathrm{OC}\:\:\measuredangle\mathrm{COD}=\mathrm{45}° \\ $$$$\bigtriangleup\mathrm{OAE}\:\:\mathrm{et}\:\:\bigtriangleup\mathrm{BCD}\:\left(\:\mathrm{triangles}\:\mathrm{rectangles}\right) \\ $$$$\mathrm{OB}=\mathrm{BD}=\mathrm{BC}\Rightarrow{a}+{b}={c}\:\left(\mathrm{1}\right) \\ $$$$\mathrm{cos}\:\mathrm{45}=\frac{{a}}{\mathrm{2}{r}}=\frac{{a}+{b}}{\mathrm{3}{r}}\:,\:\:\frac{{a}}{\mathrm{2}}=\frac{{a}+{b}}{\mathrm{3}}\:\Rightarrow\:\frac{{a}}{{b}}=\mathrm{2}\:\:\:\:\:\left(\mathrm{2}\right) \\ $$$$\:\frac{{a}}{{b}}\sqrt{\frac{{c}}{{a}+{b}}}\:=\mathrm{2} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 11/Nov/22
Commented by Acem last updated on 12/Nov/22
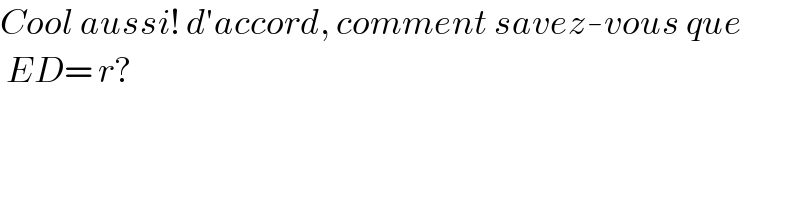
Cool aussi! d′accord, comment savez-vous que ED= r?
$${Cool}\:{aussi}!\:{d}'{accord},\:{comment}\:{savez}-{vous}\:{que} \\ $$$$\:{ED}=\:{r}? \\ $$
Commented by mr W last updated on 12/Nov/22
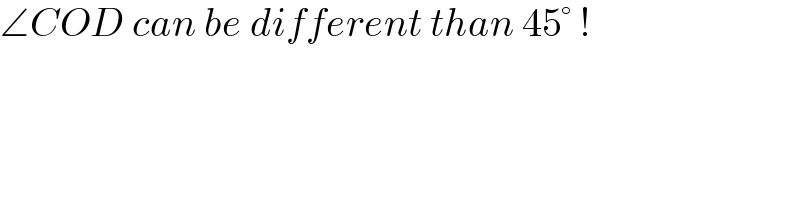
∠COD can be different than 45° !
$$\angle{COD}\:{can}\:{be}\:{different}\:{than}\:\mathrm{45}°\:! \\ $$
Commented by mr W last updated on 12/Nov/22
Answered by mr W last updated on 12/Nov/22
Commented by mr W last updated on 12/Nov/22
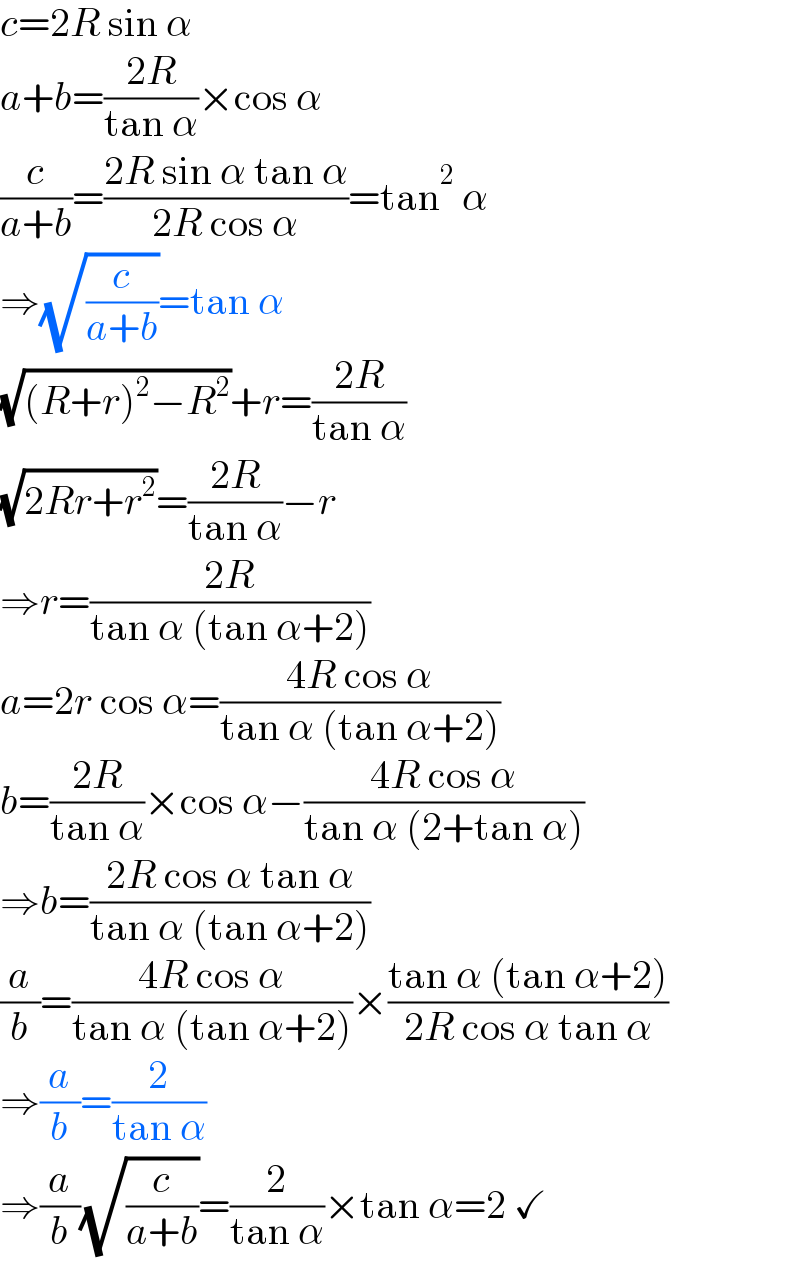
c=2R sin α a+b=((2R)/(tan α))×cos α (c/(a+b))=((2R sin α tan α)/(2R cos α))=tan^2 α ⇒(√(c/(a+b)))=tan α (√((R+r)^2 −R^2 ))+r=((2R)/(tan α)) (√(2Rr+r^2 ))=((2R)/(tan α))−r ⇒r=((2R)/(tan α (tan α+2))) a=2r cos α=((4R cos α)/(tan α (tan α+2))) b=((2R)/(tan α))×cos α−((4R cos α)/(tan α (2+tan α))) ⇒b=((2R cos α tan α)/(tan α (tan α+2))) (a/b)=((4R cos α)/(tan α (tan α+2)))×((tan α (tan α+2))/(2R cos α tan α)) ⇒(a/b)=(2/(tan α)) ⇒(a/b)(√(c/(a+b)))=(2/(tan α))×tan α=2 ✓
$${c}=\mathrm{2}{R}\:\mathrm{sin}\:\alpha \\ $$$${a}+{b}=\frac{\mathrm{2}{R}}{\mathrm{tan}\:\alpha}×\mathrm{cos}\:\alpha \\ $$$$\frac{{c}}{{a}+{b}}=\frac{\mathrm{2}{R}\:\mathrm{sin}\:\alpha\:\mathrm{tan}\:\alpha}{\mathrm{2}{R}\:\mathrm{cos}\:\alpha}=\mathrm{tan}^{\mathrm{2}} \:\alpha \\ $$$$\Rightarrow\sqrt{\frac{{c}}{{a}+{b}}}=\mathrm{tan}\:\alpha \\ $$$$\sqrt{\left({R}+{r}\right)^{\mathrm{2}} −{R}^{\mathrm{2}} }+{r}=\frac{\mathrm{2}{R}}{\mathrm{tan}\:\alpha} \\ $$$$\sqrt{\mathrm{2}{Rr}+{r}^{\mathrm{2}} }=\frac{\mathrm{2}{R}}{\mathrm{tan}\:\alpha}−{r} \\ $$$$\Rightarrow{r}=\frac{\mathrm{2}{R}}{\mathrm{tan}\:\alpha\:\left(\mathrm{tan}\:\alpha+\mathrm{2}\right)} \\ $$$${a}=\mathrm{2}{r}\:\mathrm{cos}\:\alpha=\frac{\mathrm{4}{R}\:\mathrm{cos}\:\alpha}{\mathrm{tan}\:\alpha\:\left(\mathrm{tan}\:\alpha+\mathrm{2}\right)} \\ $$$${b}=\frac{\mathrm{2}{R}}{\mathrm{tan}\:\alpha}×\mathrm{cos}\:\alpha−\frac{\mathrm{4}{R}\:\mathrm{cos}\:\alpha}{\mathrm{tan}\:\alpha\:\left(\mathrm{2}+\mathrm{tan}\:\alpha\right)} \\ $$$$\Rightarrow{b}=\frac{\mathrm{2}{R}\:\mathrm{cos}\:\alpha\:\mathrm{tan}\:\alpha}{\mathrm{tan}\:\alpha\:\left(\mathrm{tan}\:\alpha+\mathrm{2}\right)} \\ $$$$\frac{{a}}{{b}}=\frac{\mathrm{4}{R}\:\mathrm{cos}\:\alpha}{\mathrm{tan}\:\alpha\:\left(\mathrm{tan}\:\alpha+\mathrm{2}\right)}×\frac{\mathrm{tan}\:\alpha\:\left(\mathrm{tan}\:\alpha+\mathrm{2}\right)}{\mathrm{2}{R}\:\mathrm{cos}\:\alpha\:\mathrm{tan}\:\alpha} \\ $$$$\Rightarrow\frac{{a}}{{b}}=\frac{\mathrm{2}}{\mathrm{tan}\:\alpha} \\ $$$$\Rightarrow\frac{{a}}{{b}}\sqrt{\frac{{c}}{{a}+{b}}}=\frac{\mathrm{2}}{\mathrm{tan}\:\alpha}×\mathrm{tan}\:\alpha=\mathrm{2}\:\checkmark \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *