Question-180301

Question Number 180301 by Noorzai last updated on 10/Nov/22

Commented by MJS_new last updated on 10/Nov/22

this has the shape a^x +(1/a^x )=b^x which we can solve for b: b=((a^x +(1/a^x )))^(1/x) and for a: a^x +(1/a^x )=2cosh (xln a) =b^x ⇒ a=e^((cosh^(−1) (b^x /2))/x) but we cannot solve for x. we can { ((always approximate)),((sometimes see an obvious solution)) :}

$$\mathrm{this}\:\mathrm{has}\:\mathrm{the}\:\mathrm{shape} \\ $$$${a}^{{x}} +\frac{\mathrm{1}}{{a}^{{x}} }={b}^{{x}} \\ $$$$\mathrm{which}\:\mathrm{we}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{for}\:{b}: \\ $$$${b}=\sqrt[{{x}}]{{a}^{{x}} +\frac{\mathrm{1}}{{a}^{{x}} }} \\ $$$$\mathrm{and}\:\mathrm{for}\:{a}: \\ $$$${a}^{{x}} +\frac{\mathrm{1}}{{a}^{{x}} }=\mathrm{2cosh}\:\left({x}\mathrm{ln}\:{a}\right)\:={b}^{{x}} \\ $$$$\Rightarrow\:{a}=\mathrm{e}^{\frac{\mathrm{cosh}^{−\mathrm{1}} \:\frac{{b}^{{x}} }{\mathrm{2}}}{{x}}} \\ $$$$\mathrm{but}\:\mathrm{we}\:\mathrm{cannot}\:\mathrm{solve}\:\mathrm{for}\:{x}. \\ $$$$\mathrm{we}\:\mathrm{can}\:\begin{cases}{\mathrm{always}\:\mathrm{approximate}}\\{\mathrm{sometimes}\:\mathrm{see}\:\mathrm{an}\:\mathrm{obvious}\:\mathrm{solution}}\end{cases} \\ $$

Answered by MJS_new last updated on 10/Nov/22

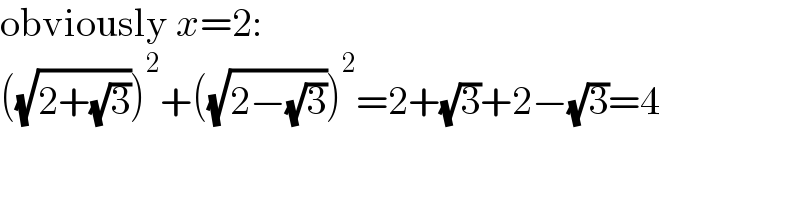
obviously x=2: ((√(2+(√3))))^2 +((√(2−(√3))))^2 =2+(√3)+2−(√3)=4

$$\mathrm{obviously}\:{x}=\mathrm{2}: \\ $$$$\left(\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} +\left(\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\right)^{\mathrm{2}} =\mathrm{2}+\sqrt{\mathrm{3}}+\mathrm{2}−\sqrt{\mathrm{3}}=\mathrm{4} \\ $$

Commented by peter frank last updated on 10/Nov/22

$$\mathrm{how}? \\ $$

Commented by MJS_new last updated on 10/Nov/22

((√t))^2 =t what else do you need to know?

$$\left(\sqrt{{t}}\right)^{\mathrm{2}} ={t} \\ $$$$\mathrm{what}\:\mathrm{else}\:\mathrm{do}\:\mathrm{you}\:\mathrm{need}\:\mathrm{to}\:\mathrm{know}? \\ $$

Answered by Rasheed.Sindhi last updated on 10/Nov/22

((√((2+(√3) )/(2−(√3)))) )^x +1=((2/( (√(2−(√3))) )))^x ((√(((2+(√3) )/(2−(√3)))×((2+(√3))/(2+(√3) )))) )^x +1=((2/( (√(2−(√3))) ))×(((√(2+(√3))) )/( (√(2+(√3))))))^x (2+(√3) )^x +1=(2(√(2+(√3))) )^x (2+(√3) )^x −(2(√(2+(√3))) )^x +1=0 (2+(√3) )^x −(4(2+(√3) ))^(x/2) +1=0 (2+(√3) )^x −4^(x/2) (2+(√3) )^(x/2) +1=0 (2+(√3) )^(x/2) =y y^2 −4^(x/2) y+1=0 y=((4±(√(4^x −4)))/2)=(2+(√3) )^(x/2) 2±(√(4^(x−1) −1)) =(2+(√3) )^(x/2) LHS consist of two terms: non-radical & radical and non-radical=2 This is possible when (x/2)=1⇒x=2 and this satisfied also radical terms 2±(√(4^(2−1) −1)) =(2+(√3) )^(2/2) 2+(√3) =(2+(√3) )^(2/2) [ ∵2−(√3) =(2+(√3) )^(2/2) doesn′t satisy] ∴ x=2

$$\left(\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{3}}\:}{\mathrm{2}−\sqrt{\mathrm{3}}}}\:\right)^{{x}} +\mathrm{1}=\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\:}\right)^{{x}} \\ $$$$\left(\sqrt{\frac{\mathrm{2}+\sqrt{\mathrm{3}}\:}{\mathrm{2}−\sqrt{\mathrm{3}}}×\frac{\mathrm{2}+\sqrt{\mathrm{3}}}{\mathrm{2}+\sqrt{\mathrm{3}}\:}}\:\:\right)^{{x}} +\mathrm{1}=\left(\frac{\mathrm{2}}{\:\sqrt{\mathrm{2}−\sqrt{\mathrm{3}}}\:}×\frac{\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:}{\:\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}}\right)^{{x}} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}} +\mathrm{1}=\left(\mathrm{2}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:\right)^{{x}} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}} −\left(\mathrm{2}\sqrt{\mathrm{2}+\sqrt{\mathrm{3}}}\:\right)^{{x}} +\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}} −\left(\mathrm{4}\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)\right)^{{x}/\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}} −\mathrm{4}^{{x}/\mathrm{2}} \left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}/\mathrm{2}} +\mathrm{1}=\mathrm{0} \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}/\mathrm{2}} ={y} \\ $$$${y}^{\mathrm{2}} −\mathrm{4}^{{x}/\mathrm{2}} {y}+\mathrm{1}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{4}\pm\sqrt{\mathrm{4}^{{x}} −\mathrm{4}}}{\mathrm{2}}=\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}/\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{2}\pm\sqrt{\mathrm{4}^{{x}−\mathrm{1}} −\mathrm{1}}\:=\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{{x}/\mathrm{2}} \\ $$$${LHS}\:{consist}\:{of}\:{two}\:{terms}:\: \\ $$$${non}-{radical}\:\&\:{radical}\: \\ $$$${and}\:{non}-{radical}=\mathrm{2} \\ $$$${This}\:{is}\:{possible}\:{when}\: \\ $$$$\:\:\:\frac{{x}}{\mathrm{2}}=\mathrm{1}\Rightarrow{x}=\mathrm{2}\: \\ $$$${and}\:{this}\:{satisfied}\:{also}\:{radical}\:{terms} \\ $$$$\:\:\:\:\:\:\mathrm{2}\pm\sqrt{\mathrm{4}^{\mathrm{2}−\mathrm{1}} −\mathrm{1}}\:=\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}/\mathrm{2}} \\ $$$$\:\:\:\:\:\:\mathrm{2}+\sqrt{\mathrm{3}}\:=\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}/\mathrm{2}} \\ $$$$\left[\:\because\mathrm{2}−\sqrt{\mathrm{3}}\:=\left(\mathrm{2}+\sqrt{\mathrm{3}}\:\right)^{\mathrm{2}/\mathrm{2}} \:{doesn}'{t}\:{satisy}\right] \\ $$$$\therefore\:\:\:{x}=\mathrm{2} \\ $$

Answered by mr W last updated on 10/Nov/22

we know y=a^x is strictly increasing for a>1. (2+(√3))^(x/2) +(2−(√3))^(x/2) =4^(x/2) it′s obvious that x=2 is a solution. since y=(2+(√3))^(x/2) +(2−(√3))^(x/2) −4^(x/2) is strictly increasing or strictly decreasing, it has one and only one zero, so x=2 is the only solution.

$${we}\:{know}\:{y}={a}^{{x}} \:{is}\:{strictly}\:{increasing} \\ $$$${for}\:{a}>\mathrm{1}. \\ $$$$\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\frac{{x}}{\mathrm{2}}} +\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\frac{{x}}{\mathrm{2}}} =\mathrm{4}^{\frac{{x}}{\mathrm{2}}} \\ $$$${it}'{s}\:{obvious}\:{that}\:{x}=\mathrm{2}\:{is}\:{a}\:{solution}. \\ $$$${since}\:{y}=\left(\mathrm{2}+\sqrt{\mathrm{3}}\right)^{\frac{{x}}{\mathrm{2}}} +\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)^{\frac{{x}}{\mathrm{2}}} −\mathrm{4}^{\frac{{x}}{\mathrm{2}}} \\ $$$${is}\:{strictly}\:{increasing}\:{or}\:{strictly} \\ $$$${decreasing},\:{it}\:{has}\:{one}\:{and}\:{only}\:{one} \\ $$$${zero},\:{so}\:{x}=\mathrm{2}\:{is}\:{the}\:{only}\:{solution}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply