Question Number 180363 by peter frank last updated on 11/Nov/22
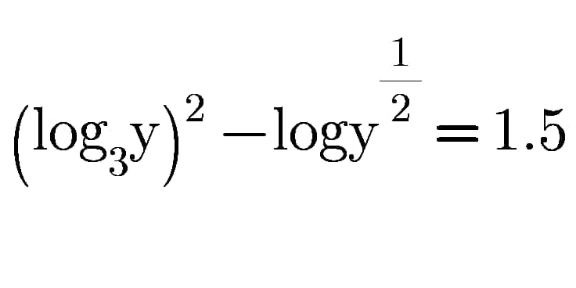
Answered by mr W last updated on 11/Nov/22
![t=y^(1/2) y=t^2 (((2 log t)/(log 3)))^2 −log t−(3/2)=0 log t=((1±(√(1+4×(4/((log 3)^2 ))×(3/2))))/(8/((log 3)^2 ))) log t=((log 3)/8)[log 3±(√((log 3)^2 +24))] ⇒y=t^2 =e^(((log 3)/4)[log 3±(√((log 3)^2 +24))])](https://www.tinkutara.com/question/Q180373.png)
$${t}={y}^{\frac{\mathrm{1}}{\mathrm{2}}} \\ $$$${y}={t}^{\mathrm{2}} \\ $$$$\left(\frac{\mathrm{2}\:\mathrm{log}\:{t}}{\mathrm{log}\:\mathrm{3}}\right)^{\mathrm{2}} −\mathrm{log}\:{t}−\frac{\mathrm{3}}{\mathrm{2}}=\mathrm{0} \\ $$$$\mathrm{log}\:{t}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}×\frac{\mathrm{4}}{\left(\mathrm{log}\:\mathrm{3}\right)^{\mathrm{2}} }×\frac{\mathrm{3}}{\mathrm{2}}}}{\frac{\mathrm{8}}{\left(\mathrm{log}\:\mathrm{3}\right)^{\mathrm{2}} }} \\ $$$$\mathrm{log}\:{t}=\frac{\mathrm{log}\:\mathrm{3}}{\mathrm{8}}\left[\mathrm{log}\:\mathrm{3}\pm\sqrt{\left(\mathrm{log}\:\mathrm{3}\right)^{\mathrm{2}} +\mathrm{24}}\right] \\ $$$$\Rightarrow{y}={t}^{\mathrm{2}} ={e}^{\frac{\mathrm{log}\:\mathrm{3}}{\mathrm{4}}\left[\mathrm{log}\:\mathrm{3}\pm\sqrt{\left(\mathrm{log}\:\mathrm{3}\right)^{\mathrm{2}} +\mathrm{24}}\right]} \\ $$
Commented by peter frank last updated on 11/Nov/22

$$\mathrm{thank}\:\mathrm{you} \\ $$
