Question Number 180457 by liuxinnan last updated on 12/Nov/22
Commented by mr W last updated on 12/Nov/22
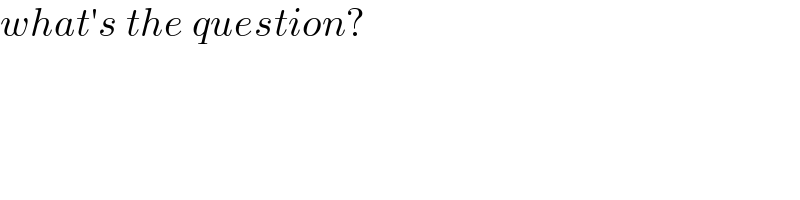
$${what}'{s}\:{the}\:{question}? \\ $$
Commented by liuxinnan last updated on 12/Nov/22
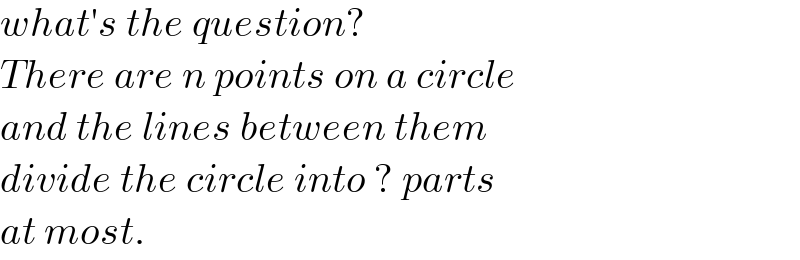
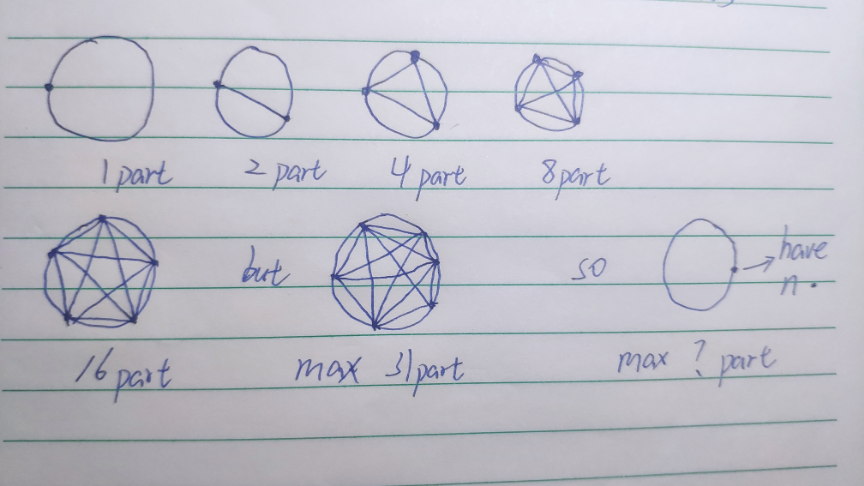
$${what}'{s}\:{the}\:{question}? \\ $$$${There}\:{are}\:{n}\:{points}\:{on}\:{a}\:{circle} \\ $$$${and}\:{the}\:{lines}\:{between}\:{them} \\ $$$${divide}\:{the}\:{circle}\:{into}\:?\:{parts} \\ $$$${at}\:{most}. \\ $$
Commented by liuxinnan last updated on 12/Nov/22
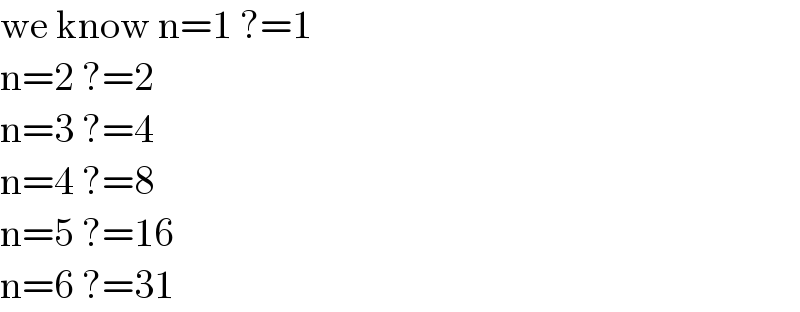
$$\mathrm{we}\:\mathrm{know}\:\mathrm{n}=\mathrm{1}\:?=\mathrm{1} \\ $$$$\mathrm{n}=\mathrm{2}\:?=\mathrm{2} \\ $$$$\mathrm{n}=\mathrm{3}\:?=\mathrm{4} \\ $$$$\mathrm{n}=\mathrm{4}\:?=\mathrm{8} \\ $$$$\mathrm{n}=\mathrm{5}\:?=\mathrm{16} \\ $$$$\mathrm{n}=\mathrm{6}\:?=\mathrm{31} \\ $$
Commented by mr W last updated on 12/Nov/22

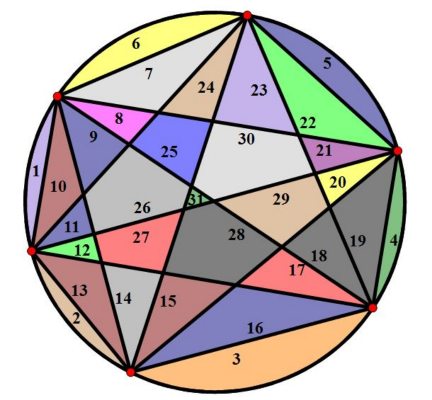
$${the}\:{general}\:\:{answer}\:{is}\: \\ $$$$\boldsymbol{{C}}_{\mathrm{4}} ^{\boldsymbol{{n}}} +\boldsymbol{{C}}_{\mathrm{2}} ^{\boldsymbol{{n}}} +\mathrm{1},\:{or}\: \\ $$$$\frac{\boldsymbol{{n}}\left(\boldsymbol{{n}}−\mathrm{1}\right)\left(\boldsymbol{{n}}^{\mathrm{2}} −\mathrm{5}\boldsymbol{{n}}+\mathrm{18}\right)}{\mathrm{24}}+\mathrm{1} \\ $$$$ \\ $$$${following}\:{article}\:{about}\:{this}\:{topic} \\ $$$${may}\:{be}\:{interesting}\:{to}\:{you}… \\ $$
Commented by mr W last updated on 12/Nov/22
Commented by mr W last updated on 12/Nov/22
http://jwilson.coe.uga.edu/EMAT6680Fa2013/Hendricks/Essay%204/Essay4.html
Commented by Emrice last updated on 12/Nov/22
$${j}'{ai}\:{aime}\:{votre}\:{article}. \\ $$
Commented by mr W last updated on 12/Nov/22

$$\mathrm{merci}\:\mathrm{beaucoup}! \\ $$
Commented by MJS_new last updated on 12/Nov/22
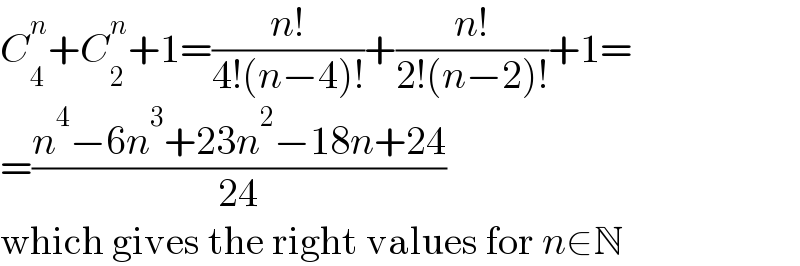
$${C}_{\mathrm{4}} ^{{n}} +{C}_{\mathrm{2}} ^{{n}} +\mathrm{1}=\frac{{n}!}{\mathrm{4}!\left({n}−\mathrm{4}\right)!}+\frac{{n}!}{\mathrm{2}!\left({n}−\mathrm{2}\right)!}+\mathrm{1}= \\ $$$$=\frac{{n}^{\mathrm{4}} −\mathrm{6}{n}^{\mathrm{3}} +\mathrm{23}{n}^{\mathrm{2}} −\mathrm{18}{n}+\mathrm{24}}{\mathrm{24}} \\ $$$$\mathrm{which}\:\mathrm{gives}\:\mathrm{the}\:\mathrm{right}\:\mathrm{values}\:\mathrm{for}\:{n}\in\mathbb{N} \\ $$
Commented by mr W last updated on 12/Nov/22

$${yes},\:{thanks}\:{sir}! \\ $$
Commented by SLVR last updated on 13/Nov/22

$${nice}\:{sir} \\ $$
Answered by Acem last updated on 12/Nov/22
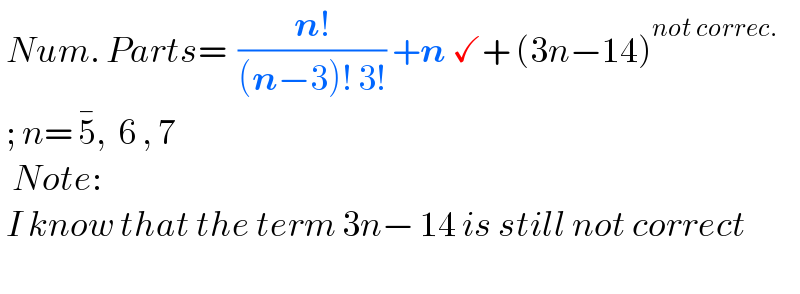
$$\:{Num}.\:{Parts}=\:\:\frac{\boldsymbol{{n}}!}{\left(\boldsymbol{{n}}−\mathrm{3}\right)!\:\mathrm{3}!}\:+\boldsymbol{{n}}\:\checkmark+\:\left(\mathrm{3}{n}−\mathrm{14}\right)^{{not}\:{correc}.} \\ $$$$\:;\:{n}=\:\bar {\mathrm{5}},\:\:\mathrm{6}\:,\:\mathrm{7} \\ $$$$\:\:{Note}: \\ $$$$\:{I}\:{know}\:{that}\:{the}\:{term}\:\mathrm{3}{n}−\:\mathrm{14}\:{is}\:{still}\:{not}\:{correct} \\ $$$$ \\ $$
Commented by liuxinnan last updated on 12/Nov/22
$${I}\:{do}\:{not}\:{know}\:{the}\:{truly}\:{answer}\:{too}.{thank}\:{you}. \\ $$
Commented by Acem last updated on 12/Nov/22

$${Thank}\:{you}\:{too}! \\ $$
