Question Number 180498 by Spillover last updated on 12/Nov/22
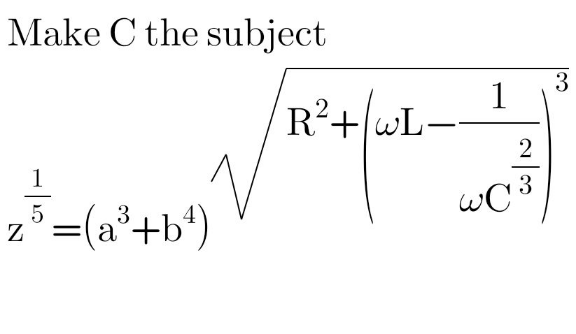
Commented by Frix last updated on 13/Nov/22
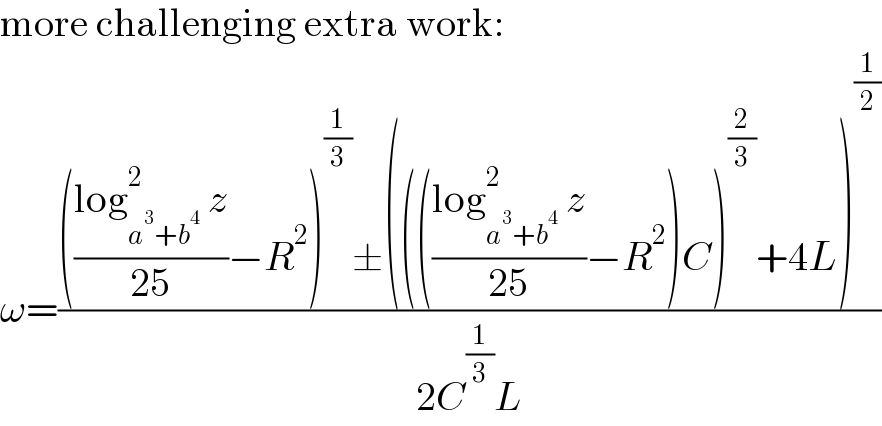
$$\mathrm{more}\:\mathrm{challenging}\:\mathrm{extra}\:\mathrm{work}: \\ $$$$\omega=\frac{\left(\frac{\mathrm{log}_{{a}^{\mathrm{3}} +{b}^{\mathrm{4}} } ^{\mathrm{2}} \:{z}}{\mathrm{25}}−{R}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \pm\left(\left(\left(\frac{\mathrm{log}_{{a}^{\mathrm{3}} +{b}^{\mathrm{4}} } ^{\mathrm{2}} \:{z}}{\mathrm{25}}−{R}^{\mathrm{2}} \right){C}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} +\mathrm{4}{L}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\mathrm{2}{C}^{\frac{\mathrm{1}}{\mathrm{3}}} {L}} \\ $$
Commented by Spillover last updated on 13/Nov/22
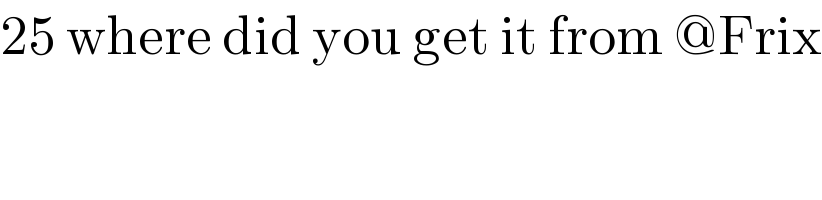
$$\mathrm{25}\:\mathrm{where}\:\mathrm{did}\:\mathrm{you}\:\mathrm{get}\:\mathrm{it}\:\mathrm{from}\:@\mathrm{Frix} \\ $$
Commented by Frix last updated on 13/Nov/22

$$\mathrm{ln}\:{z}^{\frac{\mathrm{1}}{\mathrm{5}}} =\sqrt{{term}}\mathrm{ln}\:\left({a}^{\mathrm{3}} +{b}^{\mathrm{4}} \right) \\ $$$$\frac{\mathrm{ln}\:{z}}{\mathrm{5}}=\sqrt{{term}}\mathrm{ln}\:\left({a}^{\mathrm{3}} +{b}^{\mathrm{4}} \right) \\ $$$$\frac{\mathrm{ln}\:{z}}{\mathrm{5ln}\:\left({a}^{\mathrm{3}} +{b}^{\mathrm{4}} \right)}=\sqrt{{term}} \\ $$$$\mathrm{rule}\:\frac{\mathrm{ln}\:{a}}{\mathrm{ln}\:{b}}=\mathrm{log}_{{b}} \:{a} \\ $$$$\frac{\mathrm{log}_{{a}^{\mathrm{3}} +{b}^{\mathrm{4}} } \:{z}}{\mathrm{5}}=\sqrt{{term}} \\ $$$$\frac{\mathrm{log}_{{a}^{\mathrm{3}} +{b}^{\mathrm{4}} } ^{\mathrm{2}} \:{z}}{\mathrm{25}}={term} \\ $$$$ \\ $$$$\mathrm{I}\:\mathrm{wrote}\:\mathrm{ln}\:\mathrm{instead}\:\mathrm{of}\:\mathrm{log},\:\mathrm{corrected}\:\mathrm{this}\:\mathrm{now} \\ $$
Answered by Frix last updated on 13/Nov/22
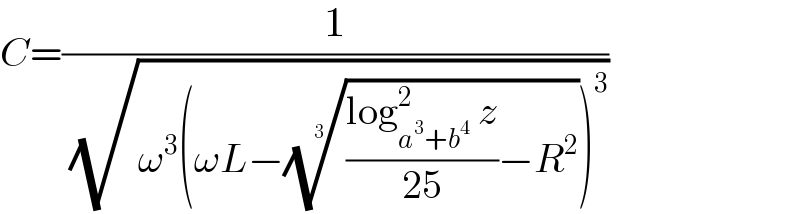
$${C}=\frac{\mathrm{1}}{\:\sqrt{\omega^{\mathrm{3}} \left(\omega{L}−\sqrt[{\mathrm{3}}]{\frac{\mathrm{log}_{{a}^{\mathrm{3}} +{b}^{\mathrm{4}} } ^{\mathrm{2}} \:{z}}{\mathrm{25}}−{R}^{\mathrm{2}} }\right)^{\mathrm{3}} }} \\ $$
Answered by floor(10²Eta[1]) last updated on 13/Nov/22

$$\mathrm{lnz}^{\mathrm{1}/\mathrm{5}} =\sqrt{\mathrm{R}^{\mathrm{2}} +\left(\omega\mathrm{L}−\frac{\mathrm{1}}{\omega\mathrm{C}^{\mathrm{2}/\mathrm{3}} }\right)^{\mathrm{3}} }\mathrm{ln}\left(\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{4}} \right) \\ $$$$\left(\frac{\mathrm{lnz}^{\mathrm{1}/\mathrm{5}} }{\mathrm{ln}\left(\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{4}} \right)}\right)^{\mathrm{2}} =\mathrm{R}^{\mathrm{2}} +\left(\omega\mathrm{L}−\frac{\mathrm{1}}{\omega\mathrm{C}^{\mathrm{2}/\mathrm{3}} }\right)^{\mathrm{3}} \\ $$$$\sqrt[{\mathrm{3}}]{\left(\frac{\mathrm{lnz}^{\mathrm{1}/\mathrm{5}} }{\mathrm{ln}\left(\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{4}} \right)}\right)^{\mathrm{2}} −\mathrm{R}^{\mathrm{2}} }=\omega\mathrm{L}−\frac{\mathrm{1}}{\omega\mathrm{C}^{\mathrm{2}/\mathrm{3}} } \\ $$$$\frac{\mathrm{1}}{\omega\mathrm{C}^{\mathrm{2}/\mathrm{3}} }=\omega\mathrm{L}−\sqrt[{\mathrm{3}}]{\left(\frac{\mathrm{lnz}^{\mathrm{1}/\mathrm{5}} }{\mathrm{ln}\left(\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{4}} \right)}\right)^{\mathrm{2}} −\mathrm{R}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{C}^{\mathrm{2}/\mathrm{3}} }=\omega^{\mathrm{2}} \mathrm{L}−\omega\sqrt[{\mathrm{3}}]{\left(\frac{\mathrm{lnz}^{\mathrm{1}/\mathrm{5}} }{\mathrm{ln}\left(\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{4}} \right)}\right)^{\mathrm{2}} −\mathrm{R}^{\mathrm{2}} } \\ $$$$\mathrm{C}^{\mathrm{2}/\mathrm{3}} =\frac{\mathrm{1}}{\omega^{\mathrm{2}} \mathrm{L}−\omega\sqrt[{\mathrm{3}}]{\left(\frac{\mathrm{lnz}^{\mathrm{1}/\mathrm{5}} }{\mathrm{ln}\left(\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{4}} \right)}\right)^{\mathrm{2}} −\mathrm{R}^{\mathrm{2}} }} \\ $$$$\mathrm{C}=\frac{\mathrm{1}}{\:\sqrt{\left(\omega^{\mathrm{2}} \mathrm{L}−\omega\sqrt[{\mathrm{3}}]{\left(\frac{\mathrm{lnz}^{\mathrm{1}/\mathrm{5}} }{\mathrm{ln}\left(\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{4}} \right)}\right)^{\mathrm{2}} −\mathrm{R}^{\mathrm{2}} }\right)^{\mathrm{3}} }} \\ $$$$ \\ $$
Commented by Spillover last updated on 13/Nov/22

$$\mathrm{great}. \\ $$
