Question Number 180509 by yaslm last updated on 13/Nov/22
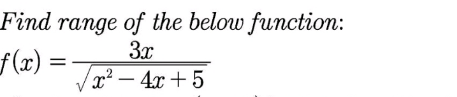
Answered by MJS_new last updated on 13/Nov/22
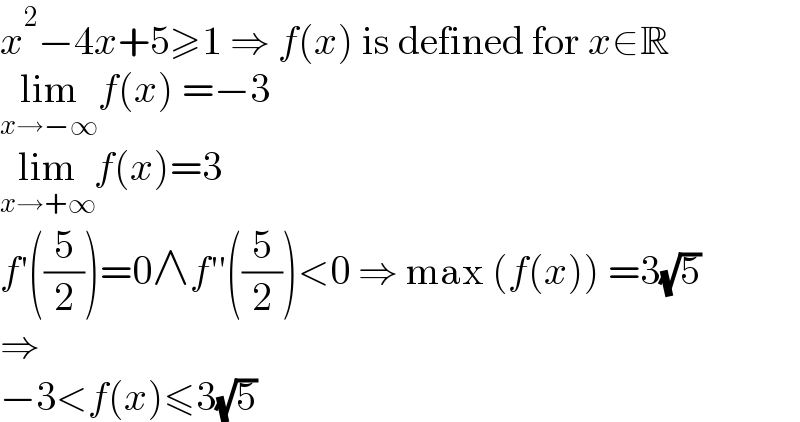
$${x}^{\mathrm{2}} −\mathrm{4}{x}+\mathrm{5}\geqslant\mathrm{1}\:\Rightarrow\:{f}\left({x}\right)\:\mathrm{is}\:\mathrm{defined}\:\mathrm{for}\:{x}\in\mathbb{R} \\ $$$$\underset{{x}\rightarrow−\infty} {\mathrm{lim}}{f}\left({x}\right)\:=−\mathrm{3} \\ $$$$\underset{{x}\rightarrow+\infty} {\mathrm{lim}}{f}\left({x}\right)=\mathrm{3} \\ $$$${f}'\left(\frac{\mathrm{5}}{\mathrm{2}}\right)=\mathrm{0}\wedge{f}''\left(\frac{\mathrm{5}}{\mathrm{2}}\right)<\mathrm{0}\:\Rightarrow\:\mathrm{max}\:\left({f}\left({x}\right)\right)\:=\mathrm{3}\sqrt{\mathrm{5}} \\ $$$$\Rightarrow \\ $$$$−\mathrm{3}<{f}\left({x}\right)\leqslant\mathrm{3}\sqrt{\mathrm{5}} \\ $$
Commented by yaslm last updated on 13/Nov/22
thank you so much
