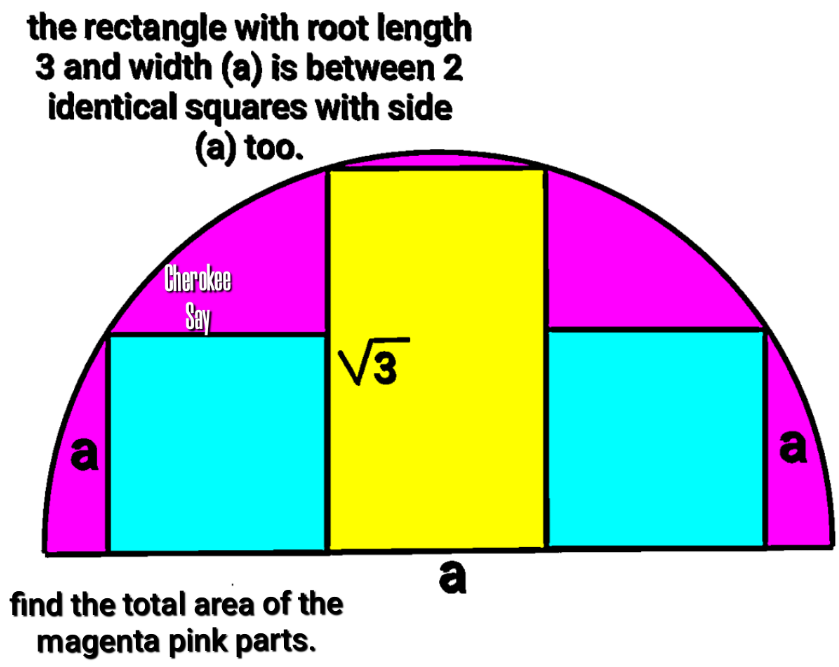
Question Number 180510 by cherokeesay last updated on 13/Nov/22
Commented by JDamian last updated on 13/Nov/22
Great roundabout expression for "yellow rectangle"
Answered by MJS_new last updated on 13/Nov/22
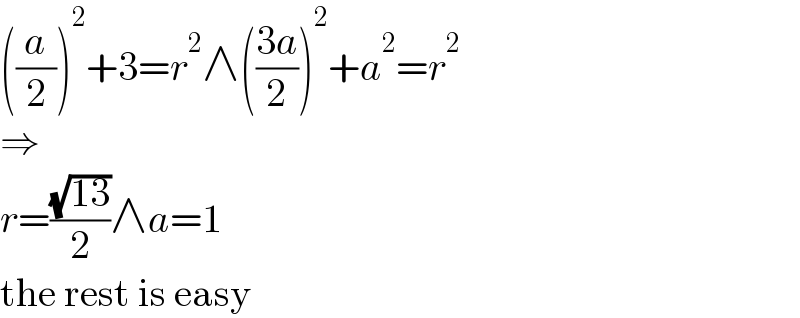
$$\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{3}={r}^{\mathrm{2}} \wedge\left(\frac{\mathrm{3}{a}}{\mathrm{2}}\right)^{\mathrm{2}} +{a}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${r}=\frac{\sqrt{\mathrm{13}}}{\mathrm{2}}\wedge{a}=\mathrm{1} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$
Answered by a.lgnaoui last updated on 13/Nov/22
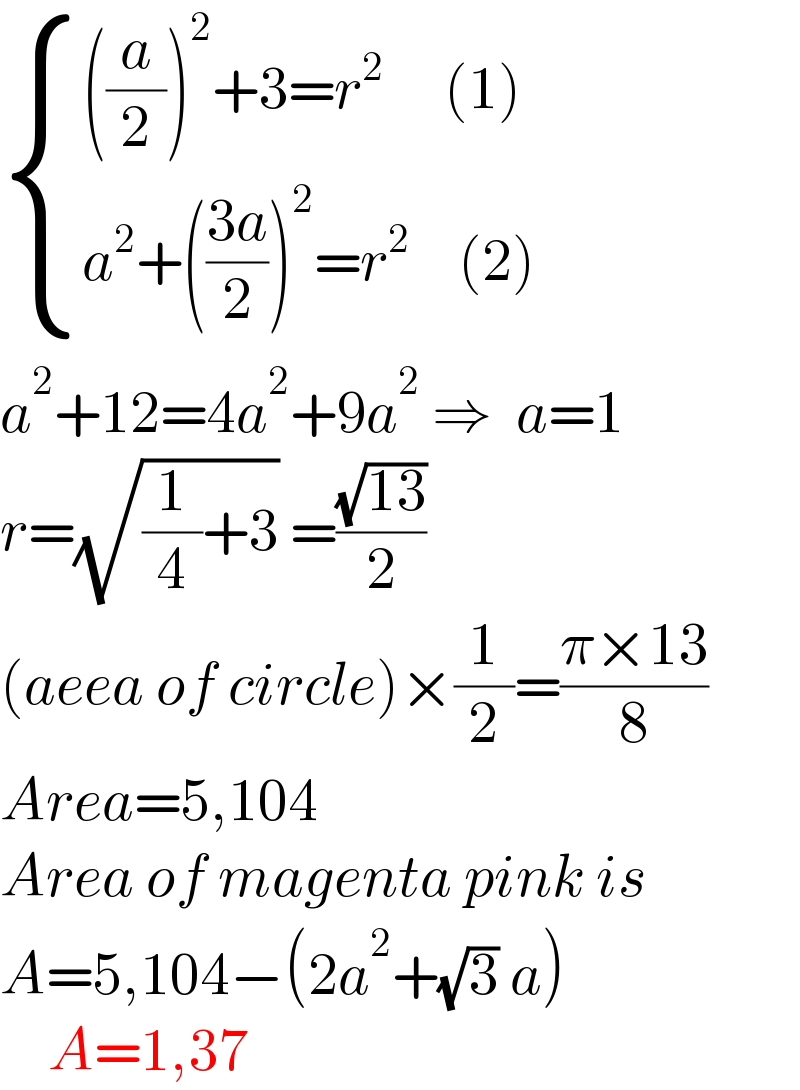
$$\begin{cases}{\left(\frac{{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{3}={r}^{\mathrm{2}} \:\:\:\:\:\left(\mathrm{1}\right)}\\{{a}^{\mathrm{2}} +\left(\frac{\mathrm{3}{a}}{\mathrm{2}}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:\:\left(\mathrm{2}\right)}\end{cases} \\ $$$${a}^{\mathrm{2}} +\mathrm{12}=\mathrm{4}{a}^{\mathrm{2}} +\mathrm{9}{a}^{\mathrm{2}} \:\Rightarrow\:\:{a}=\mathrm{1} \\ $$$${r}=\sqrt{\frac{\mathrm{1}}{\mathrm{4}}+\mathrm{3}}\:=\frac{\sqrt{\mathrm{13}}}{\mathrm{2}} \\ $$$$\left({aeea}\:{of}\:{circle}\right)×\frac{\mathrm{1}}{\mathrm{2}}=\frac{\pi×\mathrm{13}}{\mathrm{8}} \\ $$$${Area}=\mathrm{5},\mathrm{104} \\ $$$${Area}\:{of}\:{magenta}\:{pink}\:{is} \\ $$$${A}=\mathrm{5},\mathrm{104}−\left(\mathrm{2}{a}^{\mathrm{2}} +\sqrt{\mathrm{3}}\:{a}\right) \\ $$$$\:\:\:\:{A}=\mathrm{1},\mathrm{37} \\ $$
Commented by cherokeesay last updated on 13/Nov/22

$${Nice},\:{thank}\:{you} \\ $$
