Question-180547

Question Number 180547 by mnjuly1970 last updated on 13/Nov/22

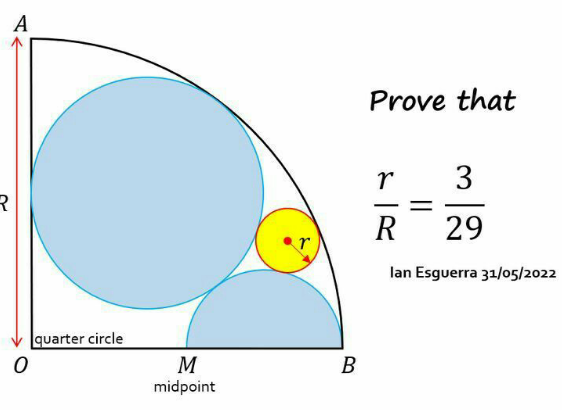
Answered by mr W last updated on 13/Nov/22

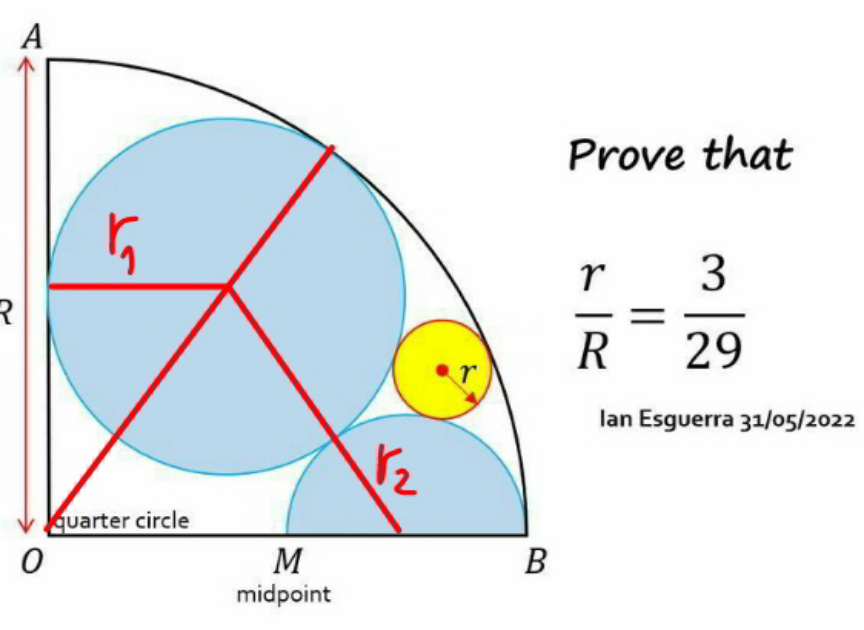
Commented by mr W last updated on 13/Nov/22

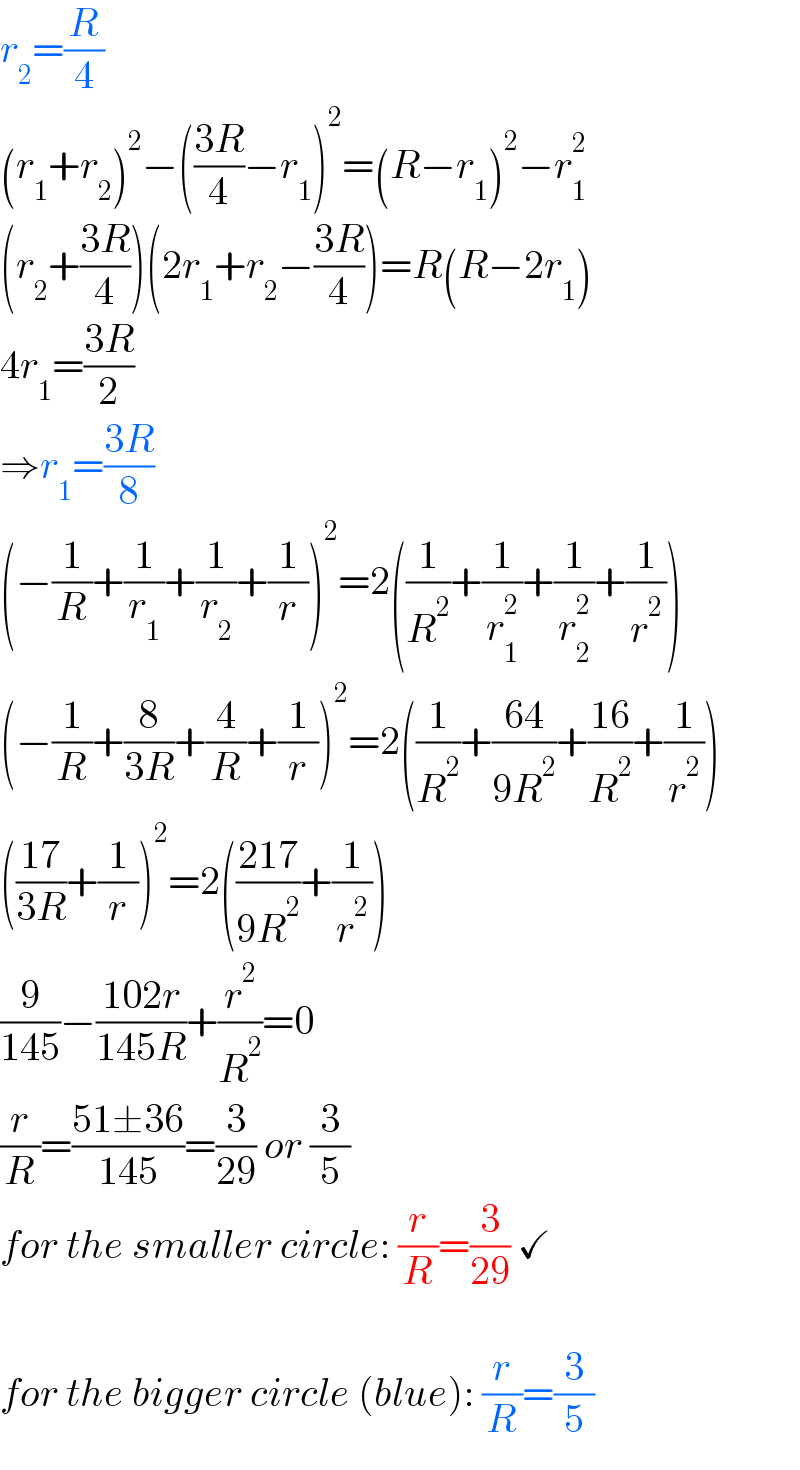
r_2 =(R/4) (r_1 +r_2 )^2 −(((3R)/4)−r_1 )^2 =(R−r_1 )^2 −r_1 ^2 (r_2 +((3R)/4))(2r_1 +r_2 −((3R)/4))=R(R−2r_1 ) 4r_1 =((3R)/2) ⇒r_1 =((3R)/8) (−(1/R)+(1/r_1 )+(1/r_2 )+(1/r))^2 =2((1/R^2 )+(1/r_1 ^2 )+(1/r_2 ^2 )+(1/r^2 )) (−(1/R)+(8/(3R))+(4/R)+(1/r))^2 =2((1/R^2 )+((64)/(9R^2 ))+((16)/R^2 )+(1/r^2 )) (((17)/(3R))+(1/r))^2 =2(((217)/(9R^2 ))+(1/r^2 )) (9/(145))−((102r)/(145R))+(r^2 /R^2 )=0 (r/R)=((51±36)/(145))=(3/(29)) or (3/5) for the smaller circle: (r/R)=(3/(29)) ✓ for the bigger circle (blue): (r/R)=(3/5)

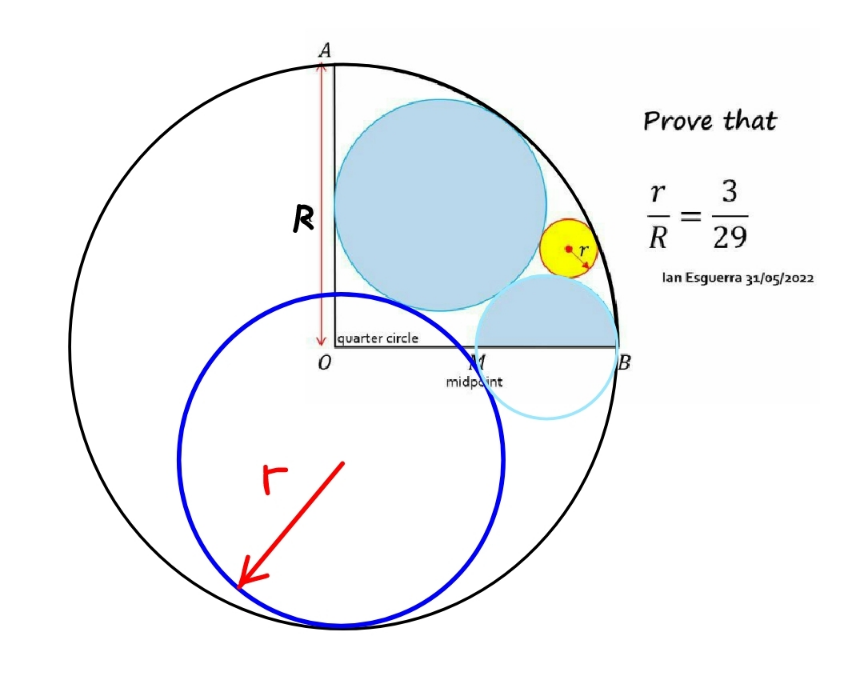
$${r}_{\mathrm{2}} =\frac{{R}}{\mathrm{4}} \\ $$$$\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{2}} −\left(\frac{\mathrm{3}{R}}{\mathrm{4}}−{r}_{\mathrm{1}} \right)^{\mathrm{2}} =\left({R}−{r}_{\mathrm{1}} \right)^{\mathrm{2}} −{r}_{\mathrm{1}} ^{\mathrm{2}} \\ $$$$\left({r}_{\mathrm{2}} +\frac{\mathrm{3}{R}}{\mathrm{4}}\right)\left(\mathrm{2}{r}_{\mathrm{1}} +{r}_{\mathrm{2}} −\frac{\mathrm{3}{R}}{\mathrm{4}}\right)={R}\left({R}−\mathrm{2}{r}_{\mathrm{1}} \right) \\ $$$$\mathrm{4}{r}_{\mathrm{1}} =\frac{\mathrm{3}{R}}{\mathrm{2}} \\ $$$$\Rightarrow{r}_{\mathrm{1}} =\frac{\mathrm{3}{R}}{\mathrm{8}} \\ $$$$\left(−\frac{\mathrm{1}}{{R}}+\frac{\mathrm{1}}{{r}_{\mathrm{1}} }+\frac{\mathrm{1}}{{r}_{\mathrm{2}} }+\frac{\mathrm{1}}{{r}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{{R}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{\mathrm{1}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}_{\mathrm{2}} ^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right) \\ $$$$\left(−\frac{\mathrm{1}}{{R}}+\frac{\mathrm{8}}{\mathrm{3}{R}}+\frac{\mathrm{4}}{{R}}+\frac{\mathrm{1}}{{r}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{1}}{{R}^{\mathrm{2}} }+\frac{\mathrm{64}}{\mathrm{9}{R}^{\mathrm{2}} }+\frac{\mathrm{16}}{{R}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right) \\ $$$$\left(\frac{\mathrm{17}}{\mathrm{3}{R}}+\frac{\mathrm{1}}{{r}}\right)^{\mathrm{2}} =\mathrm{2}\left(\frac{\mathrm{217}}{\mathrm{9}{R}^{\mathrm{2}} }+\frac{\mathrm{1}}{{r}^{\mathrm{2}} }\right) \\ $$$$\frac{\mathrm{9}}{\mathrm{145}}−\frac{\mathrm{102}{r}}{\mathrm{145}{R}}+\frac{{r}^{\mathrm{2}} }{{R}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{{r}}{{R}}=\frac{\mathrm{51}\pm\mathrm{36}}{\mathrm{145}}=\frac{\mathrm{3}}{\mathrm{29}}\:{or}\:\frac{\mathrm{3}}{\mathrm{5}} \\ $$$${for}\:{the}\:{smaller}\:{circle}:\:\frac{{r}}{{R}}=\frac{\mathrm{3}}{\mathrm{29}}\:\checkmark \\ $$$$ \\ $$$${for}\:{the}\:{bigger}\:{circle}\:\left({blue}\right):\:\frac{{r}}{{R}}=\frac{\mathrm{3}}{\mathrm{5}} \\ $$

Commented by mr W last updated on 13/Nov/22