Question Number 180554 by cherokeesay last updated on 13/Nov/22

Answered by Rasheed.Sindhi last updated on 13/Nov/22
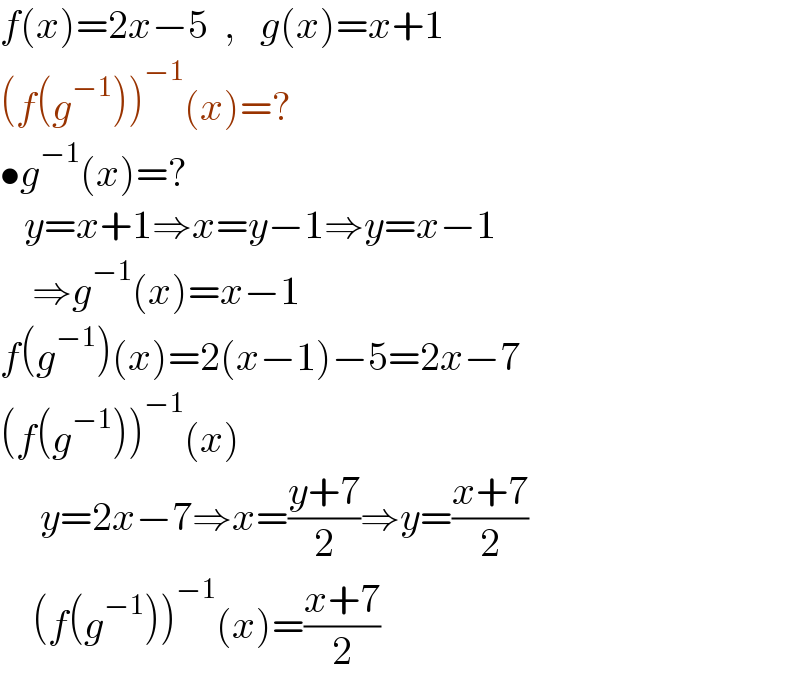
$${f}\left({x}\right)=\mathrm{2}{x}−\mathrm{5}\:\:,\:\:\:{g}\left({x}\right)={x}+\mathrm{1} \\ $$$$\left({f}\left({g}^{−\mathrm{1}} \right)\right)^{−\mathrm{1}} \left({x}\right)=? \\ $$$$\bullet{g}^{−\mathrm{1}} \left({x}\right)=? \\ $$$$\:\:\:{y}={x}+\mathrm{1}\Rightarrow{x}={y}−\mathrm{1}\Rightarrow{y}={x}−\mathrm{1} \\ $$$$\:\:\:\:\Rightarrow{g}^{−\mathrm{1}} \left({x}\right)={x}−\mathrm{1} \\ $$$${f}\left({g}^{−\mathrm{1}} \right)\left({x}\right)=\mathrm{2}\left({x}−\mathrm{1}\right)−\mathrm{5}=\mathrm{2}{x}−\mathrm{7} \\ $$$$\left({f}\left({g}^{−\mathrm{1}} \right)\right)^{−\mathrm{1}} \left({x}\right) \\ $$$$\:\:\:\:\:{y}=\mathrm{2}{x}−\mathrm{7}\Rightarrow{x}=\frac{{y}+\mathrm{7}}{\mathrm{2}}\Rightarrow{y}=\frac{{x}+\mathrm{7}}{\mathrm{2}} \\ $$$$\:\:\:\:\left({f}\left({g}^{−\mathrm{1}} \right)\right)^{−\mathrm{1}} \left({x}\right)=\frac{{x}+\mathrm{7}}{\mathrm{2}} \\ $$
Commented by cherokeesay last updated on 13/Nov/22
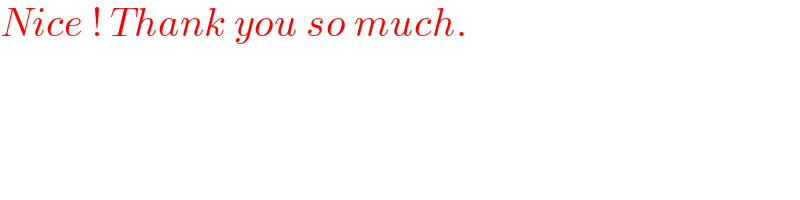
$${Nice}\:!\:{Thank}\:{you}\:{so}\:{much}. \\ $$
Answered by cortano1 last updated on 14/Nov/22
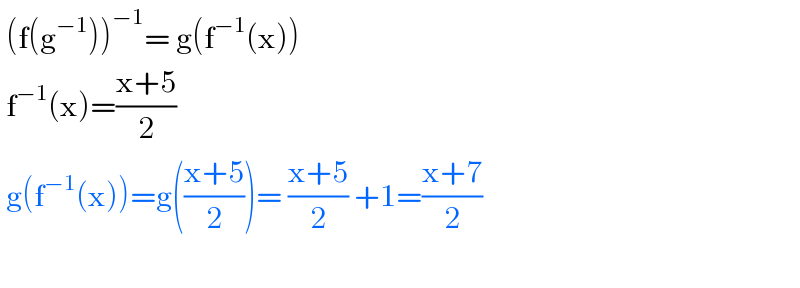
$$\:\left(\mathrm{f}\left(\mathrm{g}^{−\mathrm{1}} \right)\right)^{−\mathrm{1}} =\:\mathrm{g}\left(\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)\right) \\ $$$$\:\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)=\frac{\mathrm{x}+\mathrm{5}}{\mathrm{2}} \\ $$$$\:\mathrm{g}\left(\mathrm{f}^{−\mathrm{1}} \left(\mathrm{x}\right)\right)=\mathrm{g}\left(\frac{\mathrm{x}+\mathrm{5}}{\mathrm{2}}\right)=\:\frac{\mathrm{x}+\mathrm{5}}{\mathrm{2}}\:+\mathrm{1}=\frac{\mathrm{x}+\mathrm{7}}{\mathrm{2}} \\ $$$$ \\ $$
