Question Number 180604 by mathlove last updated on 14/Nov/22
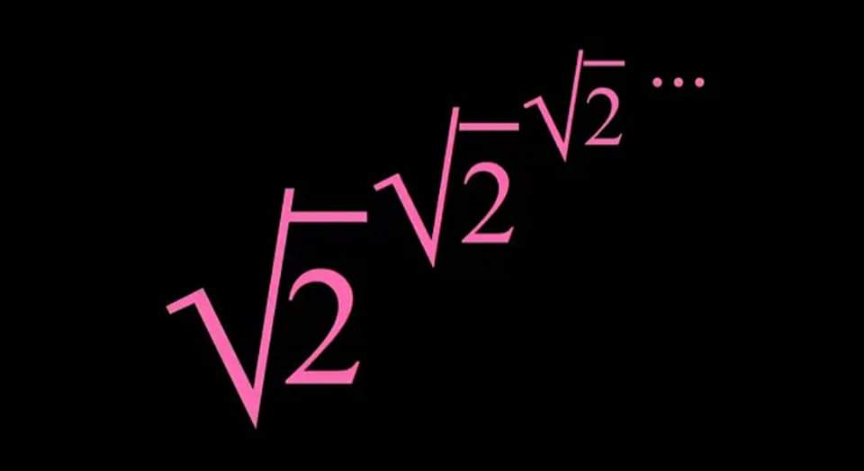
Answered by Frix last updated on 14/Nov/22
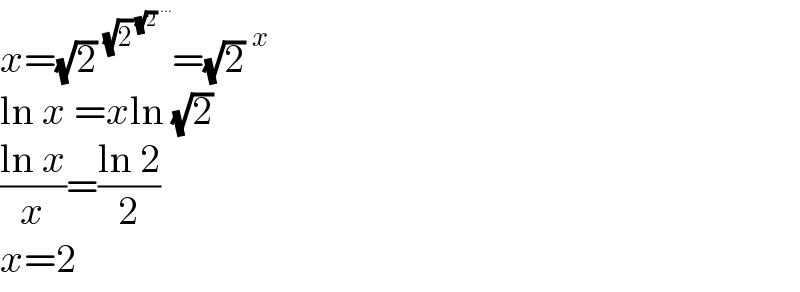
$${x}=\sqrt{\mathrm{2}}\:^{\sqrt{\mathrm{2}}\:^{\sqrt{\mathrm{2}}\:^{…} } } =\sqrt{\mathrm{2}}\:^{{x}} \\ $$$$\mathrm{ln}\:{x}\:={x}\mathrm{ln}\:\sqrt{\mathrm{2}} \\ $$$$\frac{\mathrm{ln}\:{x}}{{x}}=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}} \\ $$$${x}=\mathrm{2} \\ $$
Commented by mr W last updated on 14/Nov/22

$$\frac{\mathrm{ln}\:{x}}{{x}}=\frac{\mathrm{ln}\:\mathrm{2}}{\mathrm{2}}=\frac{\mathrm{ln}\:\mathrm{4}}{\mathrm{4}} \\ $$$${x}=\mathrm{2}\:{or}\:\mathrm{4}\:? \\ $$
Commented by Frix last updated on 14/Nov/22
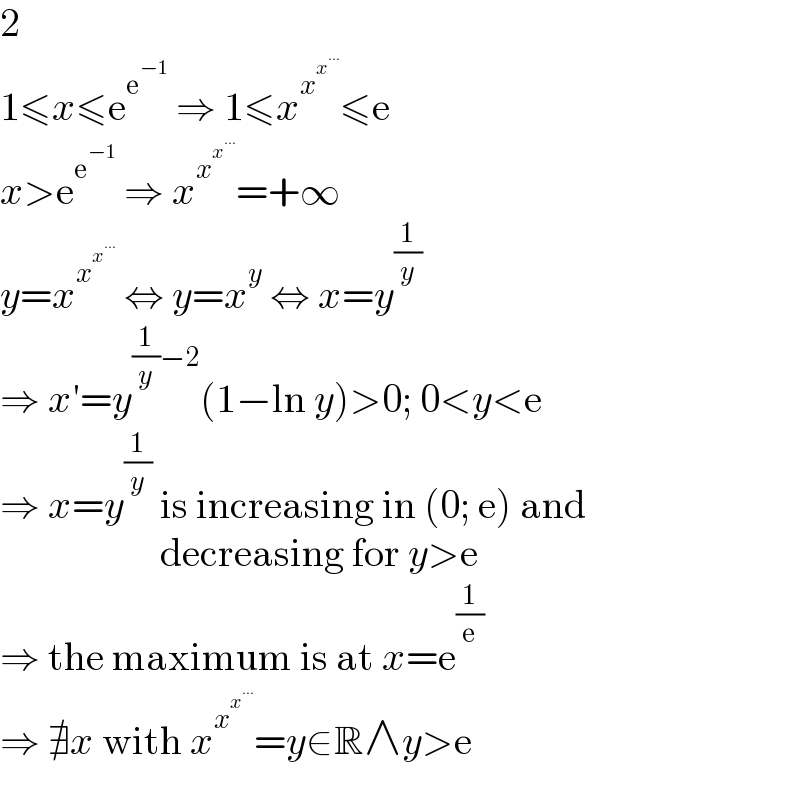
$$\mathrm{2} \\ $$$$\mathrm{1}\leqslant{x}\leqslant\mathrm{e}^{\mathrm{e}^{−\mathrm{1}} } \:\Rightarrow\:\mathrm{1}\leqslant{x}^{{x}^{{x}^{…} } } \leqslant\mathrm{e} \\ $$$${x}>\mathrm{e}^{\mathrm{e}^{−\mathrm{1}} } \:\Rightarrow\:{x}^{{x}^{{x}^{…} } } =+\infty \\ $$$${y}={x}^{{x}^{{x}^{…} } } \:\Leftrightarrow\:{y}={x}^{{y}} \:\Leftrightarrow\:{x}={y}^{\frac{\mathrm{1}}{{y}}} \\ $$$$\Rightarrow\:{x}'={y}^{\frac{\mathrm{1}}{{y}}−\mathrm{2}} \left(\mathrm{1}−\mathrm{ln}\:{y}\right)>\mathrm{0};\:\mathrm{0}<{y}<\mathrm{e} \\ $$$$\Rightarrow\:{x}={y}^{\frac{\mathrm{1}}{{y}}} \:\mathrm{is}\:\mathrm{increasing}\:\mathrm{in}\:\left(\mathrm{0};\:\mathrm{e}\right)\:\mathrm{and} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{decreasing}\:\mathrm{for}\:{y}>\mathrm{e} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{is}\:\mathrm{at}\:{x}=\mathrm{e}^{\frac{\mathrm{1}}{\mathrm{e}}} \\ $$$$\Rightarrow\:\nexists{x}\:\mathrm{with}\:{x}^{{x}^{{x}^{…} } } ={y}\in\mathbb{R}\wedge{y}>\mathrm{e} \\ $$
Commented by mathlove last updated on 15/Nov/22

$${thanks} \\ $$
