Question Number 180615 by cherokeesay last updated on 14/Nov/22

Answered by Acem last updated on 14/Nov/22
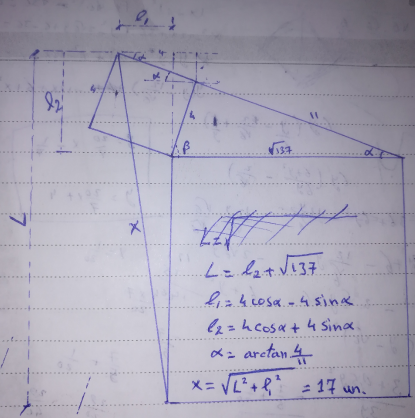
Commented by cherokeesay last updated on 14/Nov/22

$${thank}\:{you}\:{sir}. \\ $$
Answered by mr W last updated on 14/Nov/22
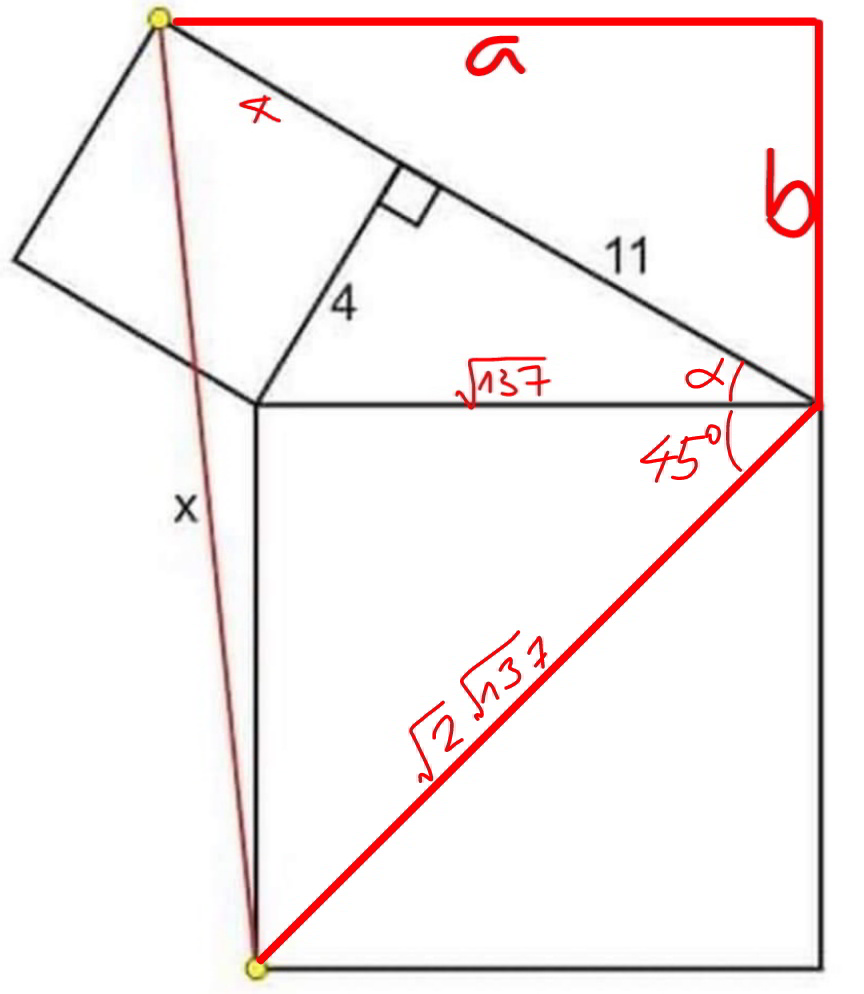
Commented by cherokeesay last updated on 14/Nov/22
$${Nice},\:{thank}\:{you}\:{sir}. \\ $$
Commented by mr W last updated on 14/Nov/22
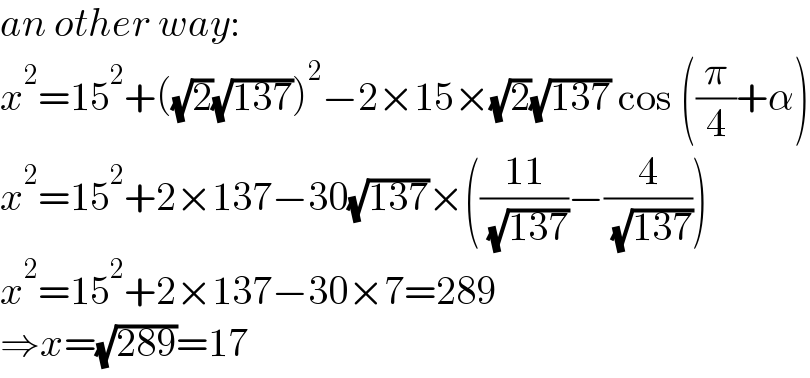
$${an}\:{other}\:{way}: \\ $$$${x}^{\mathrm{2}} =\mathrm{15}^{\mathrm{2}} +\left(\sqrt{\mathrm{2}}\sqrt{\mathrm{137}}\right)^{\mathrm{2}} −\mathrm{2}×\mathrm{15}×\sqrt{\mathrm{2}}\sqrt{\mathrm{137}}\:\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}+\alpha\right) \\ $$$${x}^{\mathrm{2}} =\mathrm{15}^{\mathrm{2}} +\mathrm{2}×\mathrm{137}−\mathrm{30}\sqrt{\mathrm{137}}×\left(\frac{\mathrm{11}}{\:\sqrt{\mathrm{137}}}−\frac{\mathrm{4}}{\:\sqrt{\mathrm{137}}}\right) \\ $$$${x}^{\mathrm{2}} =\mathrm{15}^{\mathrm{2}} +\mathrm{2}×\mathrm{137}−\mathrm{30}×\mathrm{7}=\mathrm{289} \\ $$$$\Rightarrow{x}=\sqrt{\mathrm{289}}=\mathrm{17} \\ $$
Commented by mr W last updated on 14/Nov/22
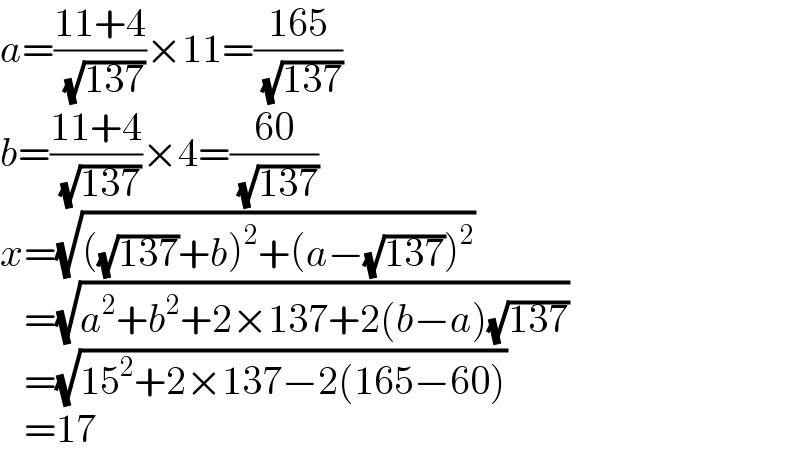
$${a}=\frac{\mathrm{11}+\mathrm{4}}{\:\sqrt{\mathrm{137}}}×\mathrm{11}=\frac{\mathrm{165}}{\:\sqrt{\mathrm{137}}} \\ $$$${b}=\frac{\mathrm{11}+\mathrm{4}}{\:\sqrt{\mathrm{137}}}×\mathrm{4}=\frac{\mathrm{60}}{\:\sqrt{\mathrm{137}}} \\ $$$${x}=\sqrt{\left(\sqrt{\mathrm{137}}+{b}\right)^{\mathrm{2}} +\left({a}−\sqrt{\mathrm{137}}\right)^{\mathrm{2}} } \\ $$$$\:\:\:=\sqrt{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} +\mathrm{2}×\mathrm{137}+\mathrm{2}\left({b}−{a}\right)\sqrt{\mathrm{137}}} \\ $$$$\:\:\:=\sqrt{\mathrm{15}^{\mathrm{2}} +\mathrm{2}×\mathrm{137}−\mathrm{2}\left(\mathrm{165}−\mathrm{60}\right)} \\ $$$$\:\:\:=\mathrm{17} \\ $$
Answered by manxsol last updated on 16/Nov/22

