Question-180621

Question Number 180621 by Noorzai last updated on 14/Nov/22

Answered by cortano1 last updated on 14/Nov/22

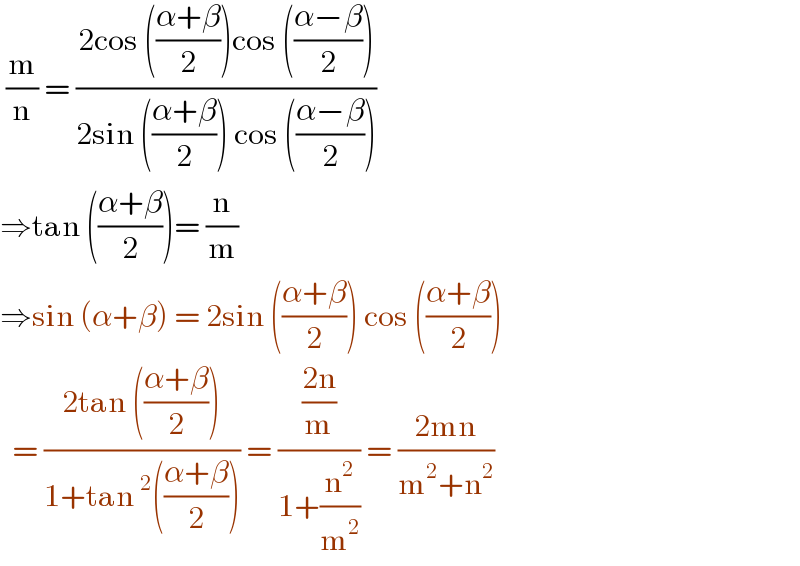
(m/n) = ((2cos (((α+β)/2))cos (((α−β)/2)))/(2sin (((α+β)/2)) cos (((α−β)/2)))) ⇒tan (((α+β)/2))= (n/m) ⇒sin (α+β) = 2sin (((α+β)/2)) cos (((α+β)/2)) = ((2tan (((α+β)/2)))/(1+tan^2 (((α+β)/2)))) = (((2n)/m)/(1+(n^2 /m^2 ))) = ((2mn)/(m^2 +n^2 ))

$$\:\frac{\mathrm{m}}{\mathrm{n}}\:=\:\frac{\mathrm{2cos}\:\left(\frac{\alpha+\beta}{\mathrm{2}}\right)\mathrm{cos}\:\left(\frac{\alpha−\beta}{\mathrm{2}}\right)}{\mathrm{2sin}\:\left(\frac{\alpha+\beta}{\mathrm{2}}\right)\:\mathrm{cos}\:\left(\frac{\alpha−\beta}{\mathrm{2}}\right)} \\ $$$$\Rightarrow\mathrm{tan}\:\left(\frac{\alpha+\beta}{\mathrm{2}}\right)=\:\frac{\mathrm{n}}{\mathrm{m}} \\ $$$$\Rightarrow\mathrm{sin}\:\left(\alpha+\beta\right)\:=\:\mathrm{2sin}\:\left(\frac{\alpha+\beta}{\mathrm{2}}\right)\:\mathrm{cos}\:\left(\frac{\alpha+\beta}{\mathrm{2}}\right) \\ $$$$\:\:=\:\frac{\mathrm{2tan}\:\left(\frac{\alpha+\beta}{\mathrm{2}}\right)}{\mathrm{1}+\mathrm{tan}\:^{\mathrm{2}} \left(\frac{\alpha+\beta}{\mathrm{2}}\right)}\:=\:\frac{\frac{\mathrm{2n}}{\mathrm{m}}}{\mathrm{1}+\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{m}^{\mathrm{2}} }}\:=\:\frac{\mathrm{2mn}}{\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} } \\ $$

Facebook Tweet Pin

Question-180621

Leave a Reply Cancel reply