Question-180653

Question Number 180653 by Shrinava last updated on 14/Nov/22

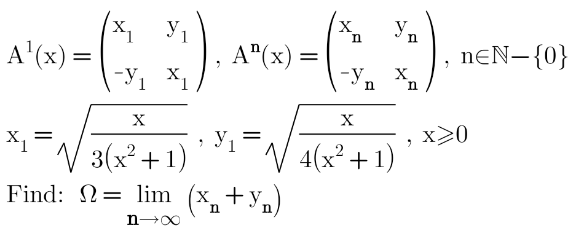
Answered by aleks041103 last updated on 17/Nov/22

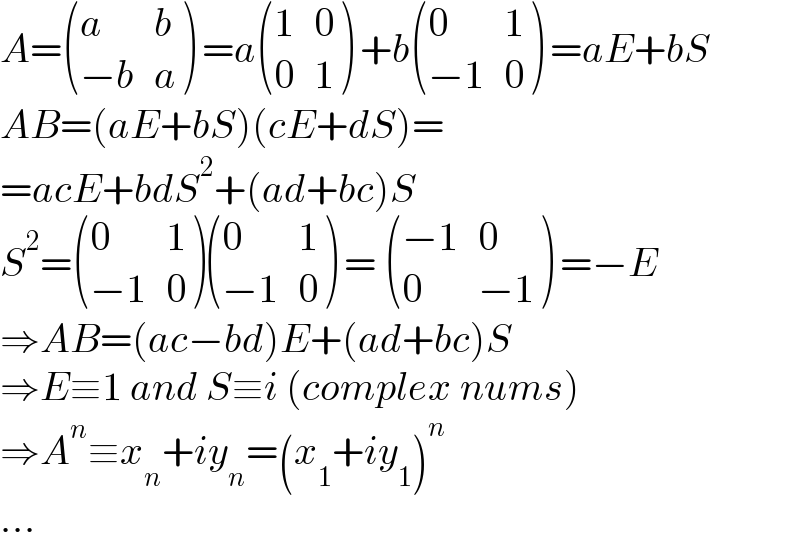
A= ((a,b),((−b),a) ) =a ((1,0),(0,1) ) +b ((0,1),((−1),0) ) =aE+bS AB=(aE+bS)(cE+dS)= =acE+bdS^2 +(ad+bc)S S^2 = ((0,1),((−1),0) ) ((0,1),((−1),0) ) = (((−1),0),(0,(−1)) ) =−E ⇒AB=(ac−bd)E+(ad+bc)S ⇒E≡1 and S≡i (complex nums) ⇒A^n ≡x_n +iy_n =(x_1 +iy_1 )^n ...

$${A}=\begin{pmatrix}{{a}}&{{b}}\\{−{b}}&{{a}}\end{pmatrix}\:={a}\begin{pmatrix}{\mathrm{1}}&{\mathrm{0}}\\{\mathrm{0}}&{\mathrm{1}}\end{pmatrix}\:+{b}\begin{pmatrix}{\mathrm{0}}&{\mathrm{1}}\\{−\mathrm{1}}&{\mathrm{0}}\end{pmatrix}\:={aE}+{bS} \\ $$$${AB}=\left({aE}+{bS}\right)\left({cE}+{dS}\right)= \\ $$$$={acE}+{bdS}^{\mathrm{2}} +\left({ad}+{bc}\right){S} \\ $$$${S}^{\mathrm{2}} =\begin{pmatrix}{\mathrm{0}}&{\mathrm{1}}\\{−\mathrm{1}}&{\mathrm{0}}\end{pmatrix}\begin{pmatrix}{\mathrm{0}}&{\mathrm{1}}\\{−\mathrm{1}}&{\mathrm{0}}\end{pmatrix}\:=\:\begin{pmatrix}{−\mathrm{1}}&{\mathrm{0}}\\{\mathrm{0}}&{−\mathrm{1}}\end{pmatrix}\:=−{E} \\ $$$$\Rightarrow{AB}=\left({ac}−{bd}\right){E}+\left({ad}+{bc}\right){S} \\ $$$$\Rightarrow{E}\equiv\mathrm{1}\:{and}\:{S}\equiv{i}\:\left({complex}\:{nums}\right) \\ $$$$\Rightarrow{A}^{{n}} \equiv{x}_{{n}} +{iy}_{{n}} =\left({x}_{\mathrm{1}} +{iy}_{\mathrm{1}} \right)^{{n}} \\ $$$$… \\ $$

Answered by aleks041103 last updated on 17/Nov/22

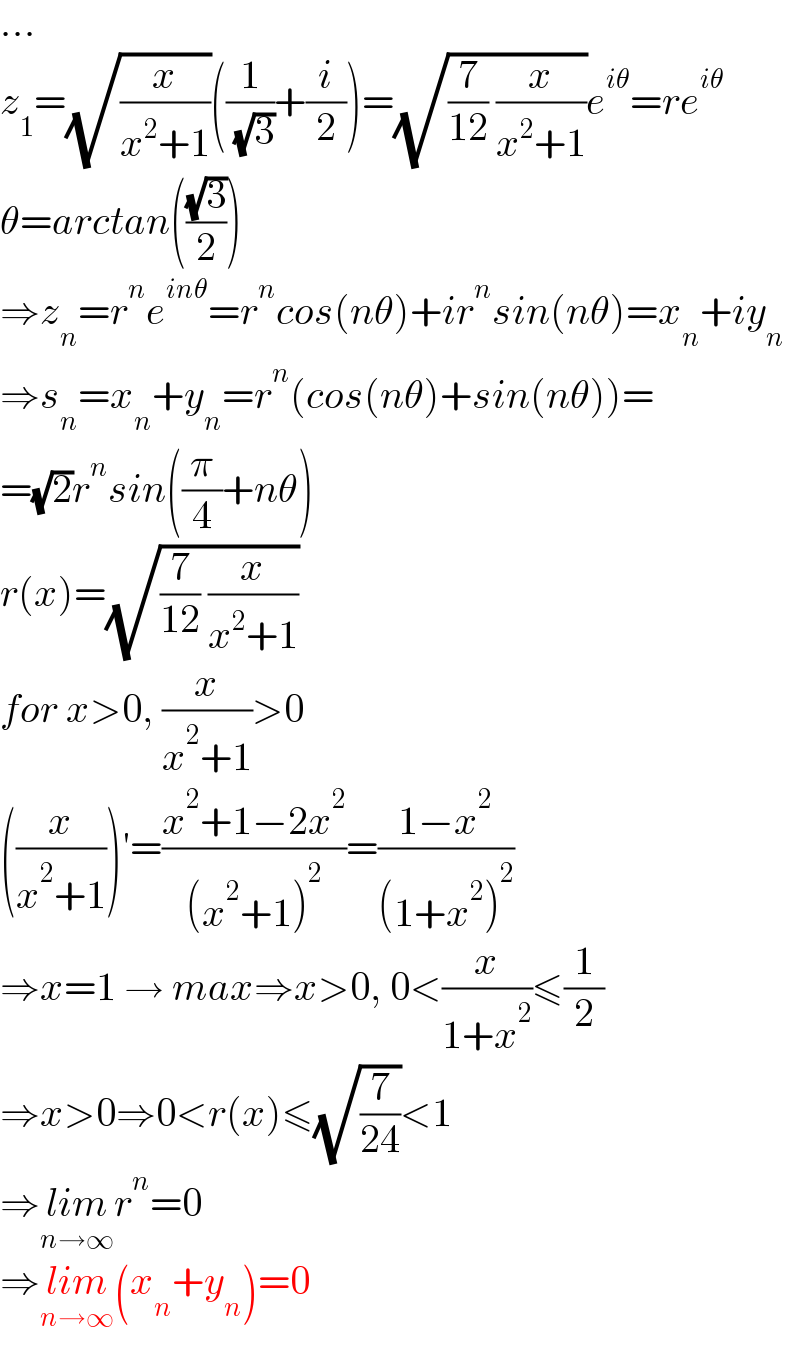
... z_1 =(√(x/(x^2 +1)))((1/( (√3)))+(i/2))=(√((7/(12)) (x/(x^2 +1))))e^(iθ) =re^(iθ) θ=arctan(((√3)/2)) ⇒z_n =r^n e^(inθ) =r^n cos(nθ)+ir^n sin(nθ)=x_n +iy_n ⇒s_n =x_n +y_n =r^n (cos(nθ)+sin(nθ))= =(√2)r^n sin((π/4)+nθ) r(x)=(√((7/(12)) (x/(x^2 +1)))) for x>0, (x/(x^2 +1))>0 ((x/(x^2 +1)))′=((x^2 +1−2x^2 )/((x^2 +1)^2 ))=((1−x^2 )/((1+x^2 )^2 )) ⇒x=1 → max⇒x>0, 0<(x/(1+x^2 ))≤(1/2) ⇒x>0⇒0<r(x)≤(√(7/(24)))<1 ⇒lim_(n→∞) r^n =0 ⇒lim_(n→∞) (x_n +y_n )=0

$$… \\ $$$${z}_{\mathrm{1}} =\sqrt{\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}+\frac{{i}}{\mathrm{2}}\right)=\sqrt{\frac{\mathrm{7}}{\mathrm{12}}\:\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}}{e}^{{i}\theta} ={re}^{{i}\theta} \\ $$$$\theta={arctan}\left(\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right) \\ $$$$\Rightarrow{z}_{{n}} ={r}^{{n}} {e}^{{in}\theta} ={r}^{{n}} {cos}\left({n}\theta\right)+{ir}^{{n}} {sin}\left({n}\theta\right)={x}_{{n}} +{iy}_{{n}} \\ $$$$\Rightarrow{s}_{{n}} ={x}_{{n}} +{y}_{{n}} ={r}^{{n}} \left({cos}\left({n}\theta\right)+{sin}\left({n}\theta\right)\right)= \\ $$$$=\sqrt{\mathrm{2}}{r}^{{n}} {sin}\left(\frac{\pi}{\mathrm{4}}+{n}\theta\right) \\ $$$${r}\left({x}\right)=\sqrt{\frac{\mathrm{7}}{\mathrm{12}}\:\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}} \\ $$$${for}\:{x}>\mathrm{0},\:\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}>\mathrm{0} \\ $$$$\left(\frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}\right)'=\frac{{x}^{\mathrm{2}} +\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} }{\left({x}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$$\Rightarrow{x}=\mathrm{1}\:\rightarrow\:{max}\Rightarrow{x}>\mathrm{0},\:\mathrm{0}<\frac{{x}}{\mathrm{1}+{x}^{\mathrm{2}} }\leqslant\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow{x}>\mathrm{0}\Rightarrow\mathrm{0}<{r}\left({x}\right)\leqslant\sqrt{\frac{\mathrm{7}}{\mathrm{24}}}<\mathrm{1} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {{lim}r}^{{n}} =\mathrm{0} \\ $$$$\Rightarrow\underset{{n}\rightarrow\infty} {{lim}}\left({x}_{{n}} +{y}_{{n}} \right)=\mathrm{0} \\ $$

Commented by Shrinava last updated on 17/Nov/22

Thank you so much dear professor, perfect

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much}\:\mathrm{dear}\:\mathrm{professor},\:\mathrm{perfect} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply