Question-180713

Question Number 180713 by Mastermind last updated on 16/Nov/22

Commented by Rasheed.Sindhi last updated on 16/Nov/22

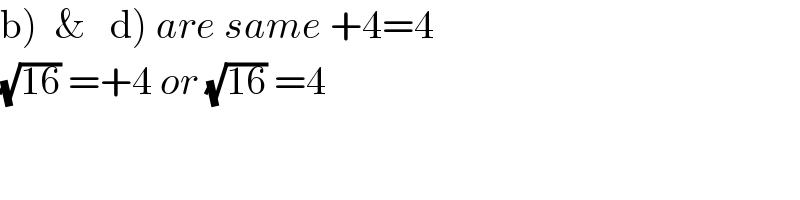
b) & d) are same +4=4 (√(16)) =+4 or (√(16)) =4

$$\left.\mathrm{b}\left.\right)\:\:\&\:\:\:\mathrm{d}\right)\:{are}\:{same}\:+\mathrm{4}=\mathrm{4} \\ $$$$\sqrt{\mathrm{16}}\:=+\mathrm{4}\:{or}\:\sqrt{\mathrm{16}}\:=\mathrm{4} \\ $$

Commented by Frix last updated on 16/Nov/22

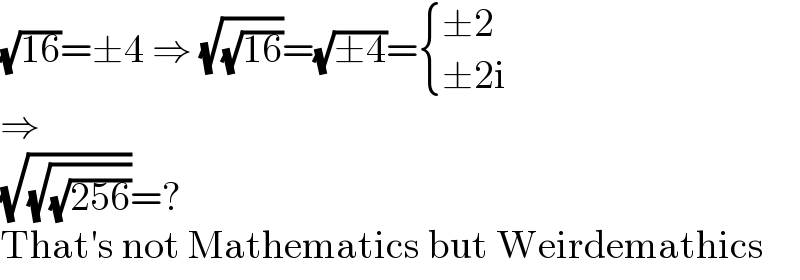
(√(16))=±4 ⇒ (√(√(16)))=(√(±4))= { ((±2)),((±2i)) :} ⇒ (√(√(√(256))))=? That′s not Mathematics but Weirdemathics

$$\sqrt{\mathrm{16}}=\pm\mathrm{4}\:\Rightarrow\:\sqrt{\sqrt{\mathrm{16}}}=\sqrt{\pm\mathrm{4}}=\begin{cases}{\pm\mathrm{2}}\\{\pm\mathrm{2i}}\end{cases} \\ $$$$\Rightarrow \\ $$$$\sqrt{\sqrt{\sqrt{\mathrm{256}}}}=? \\ $$$$\mathrm{That}'\mathrm{s}\:\mathrm{not}\:\mathrm{Mathematics}\:\mathrm{but}\:\mathrm{Weirdemathics} \\ $$

Commented by Mastermind last updated on 16/Nov/22

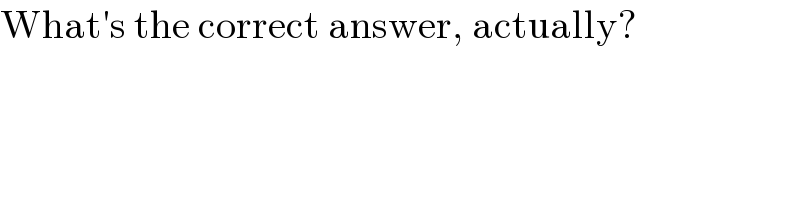
$$\mathrm{What}'\mathrm{s}\:\mathrm{the}\:\mathrm{correct}\:\mathrm{answer},\:\mathrm{actually}? \\ $$

Commented by Frix last updated on 16/Nov/22

$$\sqrt{\mathrm{16}}=\mathrm{4} \\ $$

Commented by MJS_new last updated on 16/Nov/22

I have explained this several times before, it′s annoying... (√(16)) is a simple calculation. (√(16))=4 x^2 =16 is not a calculation, here we are searching all possible numbers x which give 16 when squared. x^2 =16 ⇒ x=±(√(16))=±4 as you can see the “±” is not coming from the root, it comes before the root x^2 =16 ⇒ x= { ((−(√(16))=−4)),((+(√(16))=+4=4)) :} if (√(16))=±4 ⇒ (√(16))+(√(16))= { ((−8)),(0),(8) :}

$$\mathrm{I}\:\mathrm{have}\:\mathrm{explained}\:\mathrm{this}\:\mathrm{several}\:\mathrm{times}\:\mathrm{before}, \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{annoying}… \\ $$$$\sqrt{\mathrm{16}}\:\mathrm{is}\:\mathrm{a}\:\mathrm{simple}\:\mathrm{calculation}.\:\sqrt{\mathrm{16}}=\mathrm{4} \\ $$$${x}^{\mathrm{2}} =\mathrm{16}\:\mathrm{is}\:\mathrm{not}\:\mathrm{a}\:\mathrm{calculation},\:\mathrm{here}\:\mathrm{we}\:\mathrm{are} \\ $$$$\mathrm{searching}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{numbers}\:{x}\:\mathrm{which} \\ $$$$\mathrm{give}\:\mathrm{16}\:\mathrm{when}\:\mathrm{squared}. \\ $$$${x}^{\mathrm{2}} =\mathrm{16}\:\Rightarrow\:{x}=\pm\sqrt{\mathrm{16}}=\pm\mathrm{4} \\ $$$$\mathrm{as}\:\mathrm{you}\:\mathrm{can}\:\mathrm{see}\:\mathrm{the}\:“\pm''\:\mathrm{is}\:\mathrm{not}\:\mathrm{coming}\:\mathrm{from} \\ $$$$\mathrm{the}\:\mathrm{root},\:\mathrm{it}\:\mathrm{comes}\:{before}\:\mathrm{the}\:\mathrm{root} \\ $$$${x}^{\mathrm{2}} =\mathrm{16}\:\Rightarrow\:{x}=\begin{cases}{−\sqrt{\mathrm{16}}=−\mathrm{4}}\\{+\sqrt{\mathrm{16}}=+\mathrm{4}=\mathrm{4}}\end{cases} \\ $$$$\mathrm{if}\:\sqrt{\mathrm{16}}=\pm\mathrm{4}\:\Rightarrow\:\sqrt{\mathrm{16}}+\sqrt{\mathrm{16}}=\begin{cases}{−\mathrm{8}}\\{\mathrm{0}}\\{\mathrm{8}}\end{cases} \\ $$

Commented by Rasheed.Sindhi last updated on 16/Nov/22

@ Mastermind, see also comment of sir MJS to Q#179064 If you have had read it you need not ask this question!!!

$$@\:{Mastermind},\:{see}\:{also}\:{comment} \\ $$$${of}\:{sir}\:{MJS}\:{to}\:{Q}#\mathrm{179064} \\ $$$${If}\:{you}\:{have}\:{had}\:{read}\:{it}\:{you}\:{need}\:{not} \\ $$$${ask}\:{this}\:{question}!!! \\ $$

Commented by Mastermind last updated on 17/Nov/22

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{guys} \\ $$

Answered by Socracious last updated on 19/Nov/22

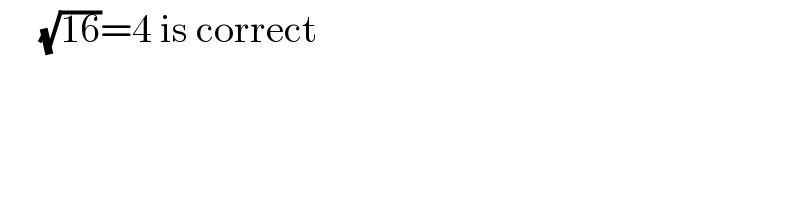
$$\:\:\:\:\:\sqrt{\mathrm{16}}=\mathrm{4}\:\mathrm{is}\:\mathrm{correct} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply