Question Number 180744 by harckinwunmy last updated on 16/Nov/22

Commented by cyathokoza last updated on 17/Nov/22

$$\boldsymbol{{I}}\:\boldsymbol{{TRY}}\:\:\:\boldsymbol{{THIS}}\:\boldsymbol{{THEN}}\:\boldsymbol{{SUBMIT}}.\:\boldsymbol{{THE}}\:\boldsymbol{{ANSWERS}} \\ $$
Commented by Acem last updated on 17/Nov/22

$${Cool} \\ $$
Answered by Acem last updated on 16/Nov/22
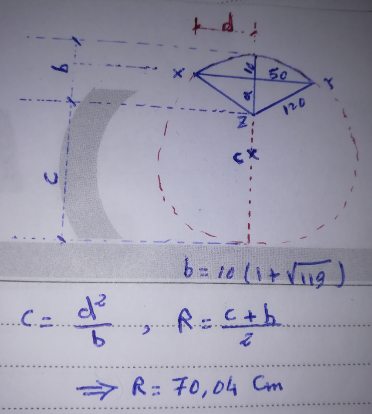
Commented by Acem last updated on 17/Nov/22
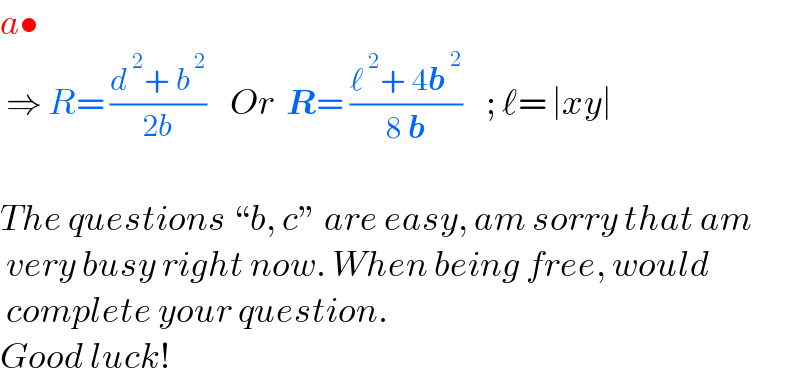
$${a}\bullet \\ $$$$\:\Rightarrow\:{R}=\:\frac{{d}^{\:\mathrm{2}} +\:{b}^{\:\mathrm{2}} }{\mathrm{2}{b}}\:\:\:\:{Or}\:\:\boldsymbol{{R}}=\:\frac{\ell^{\:\mathrm{2}} +\:\mathrm{4}\boldsymbol{{b}}^{\:\mathrm{2}} }{\mathrm{8}\:\boldsymbol{{b}}}\:\:\:\:;\:\ell=\:\mid{xy}\mid \\ $$$$ \\ $$$${The}\:{questions}\:“{b},\:{c}''\:{are}\:{easy},\:{am}\:{sorry}\:{that}\:{am} \\ $$$$\:{very}\:{busy}\:{right}\:{now}.\:{When}\:{being}\:{free},\:{would} \\ $$$$\:{complete}\:{your}\:{question}. \\ $$$${Good}\:{luck}! \\ $$
Answered by Acem last updated on 16/Nov/22
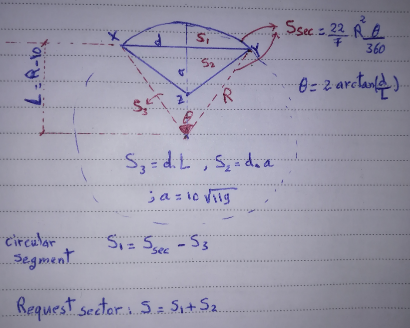
Commented by Acem last updated on 17/Nov/22

$${b}\bullet\:\:\:\:{S}_{\mathrm{1}} =\:\frac{\mathrm{11}\:\left({d}^{\:\mathrm{2}} +\:{b}^{\:\mathrm{2}} \right)^{\mathrm{2}} \:\mathrm{arctan}\:\left(\frac{{d}}{{L}}\right)}{\mathrm{2520}\:{b}^{\:\mathrm{2}} }\:−\:{d}.{L} \\ $$$$ \\ $$$${Or}\:\:\:\:\boldsymbol{{S}}_{\mathrm{1}} =\:\frac{\mathrm{11}\left(\ell^{\:\mathrm{2}} +\:\mathrm{4}\boldsymbol{{b}}^{\:\mathrm{2}} \right)^{\mathrm{2}} \:\boldsymbol{\mathrm{arctan}}\:\left(\frac{\ell}{\mathrm{2}\boldsymbol{{L}}}\right)}{\mathrm{40}\:\mathrm{320}\:\boldsymbol{{b}}^{\:\mathrm{2}} }\:−\:\frac{\mathrm{1}}{\mathrm{2}}\:\ell.\boldsymbol{{L}}\:\: \\ $$$$ \\ $$$$;\:{L}=\:\frac{\ell^{\:\mathrm{2}} +\:\mathrm{4}{b}^{\:\mathrm{2}} }{\mathrm{8}\:{b}}\:−\:{k} \\ $$$$;\:\ell=\:{Seg}.\:{wide}\:\:,\:\:{b}:\:{Seg}.\:{height}\:\:,\:\:{k}:\:{arch}\:{dome}\:{height} \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:{S}_{\mathrm{1}} =\:\mathrm{405}.\mathrm{88}\:{Cm}^{\mathrm{2}} \:\approx\:\mathrm{0}.\mathrm{0406}\:{m}^{\mathrm{2}} \\ $$$$ \\ $$$${c}\bullet\:{S}=\:{S}_{\mathrm{1}} \:+\:{d}.{a}=\:\mathrm{5}\:\mathrm{860}.\mathrm{236}\:{Cm}^{\mathrm{2}} \:\approx\:\mathrm{0}.\mathrm{58602}\:{m}^{\mathrm{2}} \\ $$$$ \\ $$
