Question Number 180746 by Acem last updated on 16/Nov/22

Answered by MJS_new last updated on 16/Nov/22
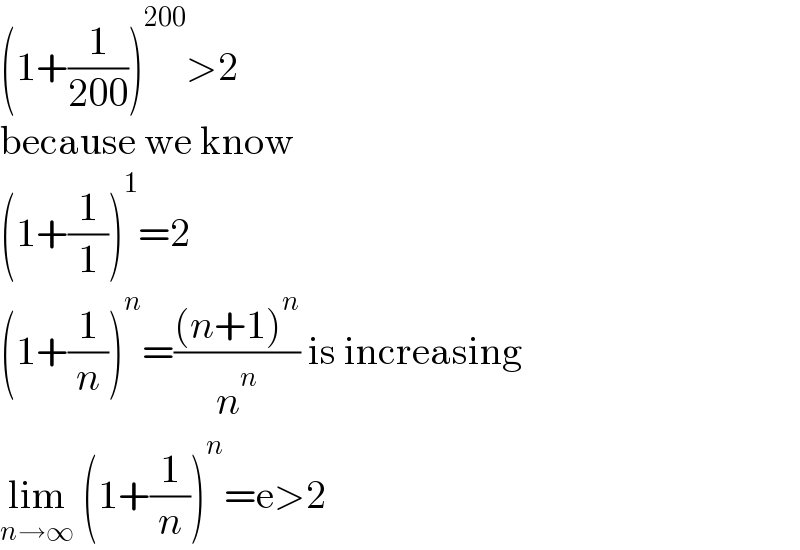
$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{200}}\right)^{\mathrm{200}} >\mathrm{2} \\ $$$$\mathrm{because}\:\mathrm{we}\:\mathrm{know} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}}\right)^{\mathrm{1}} =\mathrm{2} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} =\frac{\left({n}+\mathrm{1}\right)^{{n}} }{{n}^{{n}} }\:\mathrm{is}\:\mathrm{increasing} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} =\mathrm{e}>\mathrm{2} \\ $$
Answered by mr W last updated on 17/Nov/22
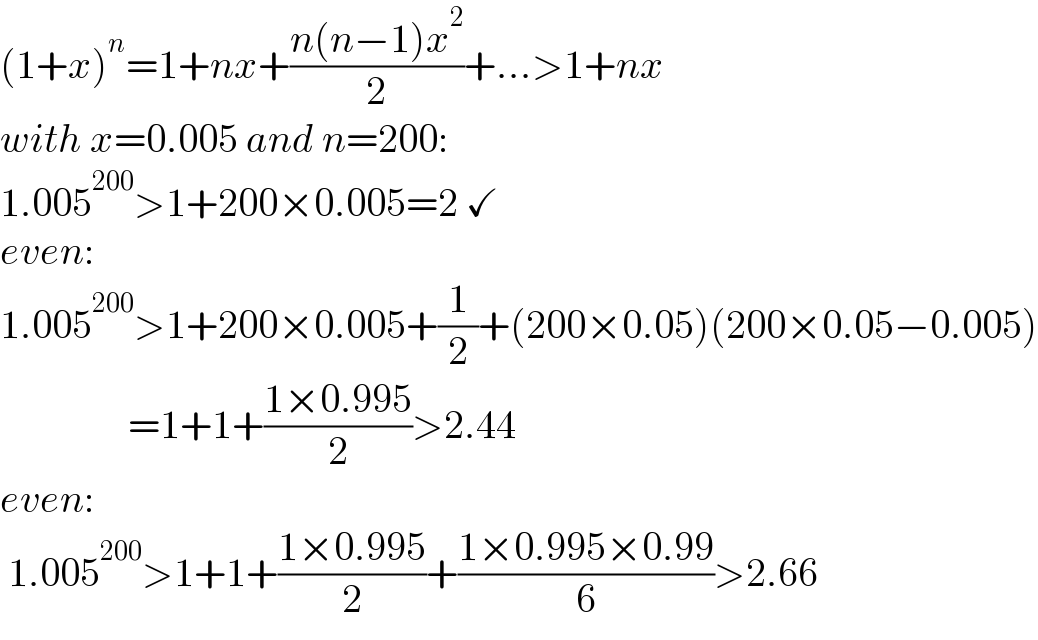
$$\left(\mathrm{1}+{x}\right)^{{n}} =\mathrm{1}+{nx}+\frac{{n}\left({n}−\mathrm{1}\right){x}^{\mathrm{2}} }{\mathrm{2}}+…>\mathrm{1}+{nx} \\ $$$${with}\:{x}=\mathrm{0}.\mathrm{005}\:{and}\:{n}=\mathrm{200}: \\ $$$$\mathrm{1}.\mathrm{005}^{\mathrm{200}} >\mathrm{1}+\mathrm{200}×\mathrm{0}.\mathrm{005}=\mathrm{2}\:\checkmark \\ $$$${even}: \\ $$$$\mathrm{1}.\mathrm{005}^{\mathrm{200}} >\mathrm{1}+\mathrm{200}×\mathrm{0}.\mathrm{005}+\frac{\mathrm{1}}{\mathrm{2}}+\left(\mathrm{200}×\mathrm{0}.\mathrm{05}\right)\left(\mathrm{200}×\mathrm{0}.\mathrm{05}−\mathrm{0}.\mathrm{005}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}+\mathrm{1}+\frac{\mathrm{1}×\mathrm{0}.\mathrm{995}}{\mathrm{2}}>\mathrm{2}.\mathrm{44} \\ $$$${even}: \\ $$$$\:\mathrm{1}.\mathrm{005}^{\mathrm{200}} >\mathrm{1}+\mathrm{1}+\frac{\mathrm{1}×\mathrm{0}.\mathrm{995}}{\mathrm{2}}+\frac{\mathrm{1}×\mathrm{0}.\mathrm{995}×\mathrm{0}.\mathrm{99}}{\mathrm{6}}>\mathrm{2}.\mathrm{66} \\ $$
Commented by manxsol last updated on 17/Nov/22

Commented by manxsol last updated on 17/Nov/22
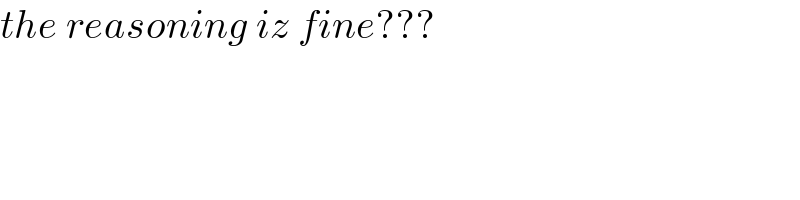
$${the}\:{reasoning}\:{iz}\:{fine}??? \\ $$
