Menu Close

Question-180756

Tinku Tara 0 Comments
Pin




Question Number 180756 by mr W last updated on 16/Nov/22
Commented by mr W last updated on 17/Nov/22
the areas of three of the six squares are given. find the area of the shaded triangle and the areas of other three squares.
$${the}\:{areas}\:{of}\:{three}\:{of}\:{the}\:{six}\:{squares} \\ $$$${are}\:{given}.\:{find}\:{the}\:{area}\:{of}\:{the}\:{shaded} \\ $$$${triangle}\:{and}\:{the}\:{areas}\:{of}\:{other}\:{three} \\ $$$${squares}. \\ $$
Answered by MJS_new last updated on 17/Nov/22
triangle with sides a, b, c ⇒ the areas of the red squares are opposite of a: 2(b^2 +c^2 )−a^2 =p^2 opposite of b: 2(a^2 +c^2 )−b^2 =q^2 opposite of c: 2(a^2 +b^2 )−c^2 =r^2 ⇔ a^2 =((2(q^2 +r^2 )−p^2 )/9) b^2 =((2(p^2 +r^2 )−q^2 )/9) c^2 =((2(p^2 +q^2 )−r^2 )/9) ⇒ area of triangle is ((√((p+q+r)(−p+q+r)(p−q+r)(p+q−r)))/(12)) which in this case is ((√(255))/4) btw a=((√(55))/3) b=((√(94))/3) c=((√(154))/3)
$$\mathrm{triangle}\:\mathrm{with}\:\mathrm{sides}\:{a},\:{b},\:{c} \\ $$$$\Rightarrow\:\mathrm{the}\:\mathrm{areas}\:\mathrm{of}\:\mathrm{the}\:\mathrm{red}\:\mathrm{squares}\:\mathrm{are} \\ $$$$\mathrm{opposite}\:\mathrm{of}\:{a}:\:\mathrm{2}\left({b}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−{a}^{\mathrm{2}} ={p}^{\mathrm{2}} \\ $$$$\mathrm{opposite}\:\mathrm{of}\:{b}:\:\mathrm{2}\left({a}^{\mathrm{2}} +{c}^{\mathrm{2}} \right)−{b}^{\mathrm{2}} ={q}^{\mathrm{2}} \\ $$$$\mathrm{opposite}\:\mathrm{of}\:{c}:\:\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)−{c}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$$\Leftrightarrow \\ $$$${a}^{\mathrm{2}} =\frac{\mathrm{2}\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)−{p}^{\mathrm{2}} }{\mathrm{9}} \\ $$$${b}^{\mathrm{2}} =\frac{\mathrm{2}\left({p}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)−{q}^{\mathrm{2}} }{\mathrm{9}} \\ $$$${c}^{\mathrm{2}} =\frac{\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)−{r}^{\mathrm{2}} }{\mathrm{9}} \\ $$$$\Rightarrow \\ $$$$\mathrm{area}\:\mathrm{of}\:\mathrm{triangle}\:\mathrm{is} \\ $$$$\frac{\sqrt{\left({p}+{q}+{r}\right)\left(−{p}+{q}+{r}\right)\left({p}−{q}+{r}\right)\left({p}+{q}−{r}\right)}}{\mathrm{12}} \\ $$$$\mathrm{which}\:\mathrm{in}\:\mathrm{this}\:\mathrm{case}\:\mathrm{is}\:\frac{\sqrt{\mathrm{255}}}{\mathrm{4}} \\ $$$$\mathrm{btw}\:{a}=\frac{\sqrt{\mathrm{55}}}{\mathrm{3}}\:\:\:\:\:{b}=\frac{\sqrt{\mathrm{94}}}{\mathrm{3}}\:\:\:\:\:{c}=\frac{\sqrt{\mathrm{154}}}{\mathrm{3}} \\ $$
Commented by mr W last updated on 17/Nov/22
thanks alot sir for the general solution!
$${thanks}\:{alot}\:{sir}\:{for}\:{the}\:{general}\:{solution}! \\ $$
Answered by a.lgnaoui last updated on 17/Nov/22
△ABC AC^2 =AB^2 +BC^2 −2AB×BCcos (((3π)/4)) 6^2 =4^2 +x^2 +4(√2)x (x=BC=BD) x^2 +4(√2) x−20=0 x=2((√7) −(√2) )=2,4630 area(BCDE)= 6,07 GH^2 =FG^2 +HF^2 −2FG×HFcos(((3π)/4)) 7^2 =4^2 +y^2 +4(√2)y y^2 +4(√2)y−33=0 y=3,57469 Aeea(Squart[GHIJ])=y^2 =12,79 Area ( triangle) : A3=((xy)/2)=((2,4630×3,5746)/2)=4,40 cote du carre [ACFH] est z^2 =x^2 +y^2 =12,79+6,07=18,86 Conclusion Area(Minimum Squart)=6,07 Area(Smal Squart)=12,79 Area(Medium Squart)= 18,86 Area(triangle)=4,40
$$\bigtriangleup{ABC}\:\:\:\mathrm{AC}^{\mathrm{2}} =\mathrm{AB}^{\mathrm{2}} +\mathrm{BC}^{\mathrm{2}} −\mathrm{2AB}×\mathrm{BCcos}\:\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{6}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +\mathrm{x}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{2}}\mathrm{x}\:\:\:\:\:\:\left(\mathrm{x}=\mathrm{BC}=\mathrm{BD}\right) \\ $$$$\mathrm{x}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{2}}\:\mathrm{x}−\mathrm{20}=\mathrm{0}\:\:\:\:\mathrm{x}=\mathrm{2}\left(\sqrt{\mathrm{7}}\:−\sqrt{\mathrm{2}}\:\right)=\mathrm{2},\mathrm{4630} \\ $$$${area}\left({BCDE}\right)=\:\mathrm{6},\mathrm{07} \\ $$$$\mathrm{GH}^{\mathrm{2}} =\mathrm{FG}^{\mathrm{2}} +\mathrm{HF}^{\mathrm{2}} −\mathrm{2FG}×\mathrm{HFcos}\left(\frac{\mathrm{3}\pi}{\mathrm{4}}\right) \\ $$$$\mathrm{7}^{\mathrm{2}} =\mathrm{4}^{\mathrm{2}} +{y}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{2}}\mathrm{y} \\ $$$$\mathrm{y}^{\mathrm{2}} +\mathrm{4}\sqrt{\mathrm{2}}\mathrm{y}−\mathrm{33}=\mathrm{0}\: \\ $$$$\:\:\mathrm{y}=\mathrm{3},\mathrm{57469} \\ $$$${Aeea}\left({Squart}\left[{GHIJ}\right]\right)={y}^{\mathrm{2}} =\mathrm{12},\mathrm{79} \\ $$$${Area}\:\left(\:{triangle}\right)\:: \\ $$$$\:\:{A}\mathrm{3}=\frac{{xy}}{\mathrm{2}}=\frac{\mathrm{2},\mathrm{4630}×\mathrm{3},\mathrm{5746}}{\mathrm{2}}=\mathrm{4},\mathrm{40} \\ $$$${cote}\:{du}\:{carre}\:\left[{ACFH}\right]\:{est} \\ $$$${z}^{\mathrm{2}} ={x}^{\mathrm{2}} +{y}^{\mathrm{2}} =\mathrm{12},\mathrm{79}+\mathrm{6},\mathrm{07}=\mathrm{18},\mathrm{86}\:\:\:\:\: \\ $$$${Conclusion} \\ $$$$ \\ $$$${Area}\left({Minimum}\:{Squart}\right)=\mathrm{6},\mathrm{07} \\ $$$${Area}\left({Smal}\:{Squart}\right)=\mathrm{12},\mathrm{79} \\ $$$${Area}\left({Medium}\:{Squart}\right)=\:\mathrm{18},\mathrm{86}\: \\ $$$${Area}\left({triangle}\right)=\mathrm{4},\mathrm{40} \\ $$$$ \\ $$
Commented by a.lgnaoui last updated on 17/Nov/22
Commented by mr W last updated on 17/Nov/22
sir: your efforts are very much to praise. but it seems that you don′t take mathematics accurately. without any argumentation you just assume the obtuse angles are ((3π)/4). i don′t think you can get the right answer in this way.
$${sir}:\:{your}\:{efforts}\:{are}\:{very}\:{much}\:{to} \\ $$$${praise}.\:{but}\:{it}\:{seems}\:{that}\:{you}\:{don}'{t}\:{take} \\ $$$${mathematics}\:{accurately}.\:{without} \\ $$$${any}\:{argumentation}\:{you}\:{just}\:{assume} \\ $$$${the}\:{obtuse}\:{angles}\:{are}\:\frac{\mathrm{3}\pi}{\mathrm{4}}.\:{i}\:{don}'{t}\:{think} \\ $$$${you}\:{can}\:{get}\:{the}\:{right}\:{answer}\:{in}\:{this} \\ $$$${way}. \\ $$
Answered by mr W last updated on 17/Nov/22
Commented by mr W last updated on 17/Nov/22
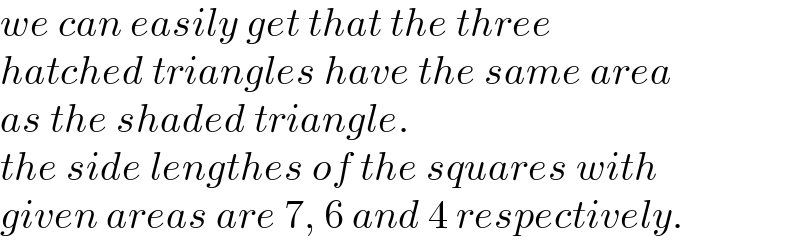
we can easily get that the three hatched triangles have the same area as the shaded triangle. the side lengthes of the squares with given areas are 7, 6 and 4 respectively.
$${we}\:{can}\:{easily}\:{get}\:{that}\:{the}\:{three} \\ $$$${hatched}\:{triangles}\:{have}\:{the}\:{same}\:{area} \\ $$$${as}\:{the}\:{shaded}\:{triangle}. \\ $$$${the}\:{side}\:{lengthes}\:{of}\:{the}\:{squares}\:{with} \\ $$$${given}\:{areas}\:{are}\:\mathrm{7},\:\mathrm{6}\:{and}\:\mathrm{4}\:{respectively}. \\ $$
Commented by mr W last updated on 17/Nov/22
Commented by mr W last updated on 17/Nov/22
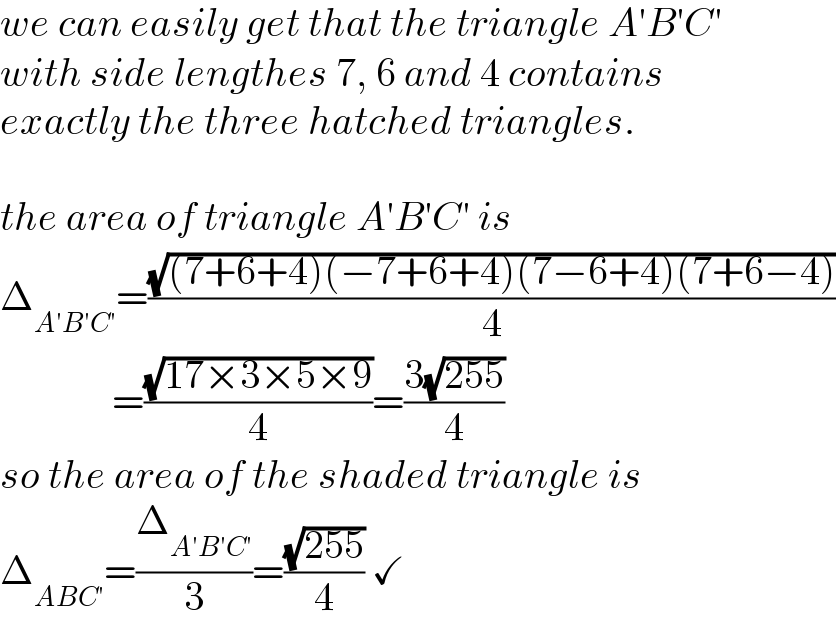
we can easily get that the triangle A′B′C′ with side lengthes 7, 6 and 4 contains exactly the three hatched triangles. the area of triangle A′B′C′ is Δ_(A′B′C′) =((√((7+6+4)(−7+6+4)(7−6+4)(7+6−4)))/4) =((√(17×3×5×9))/4)=((3(√(255)))/4) so the area of the shaded triangle is Δ_(ABC′) =(Δ_(A′B′C′) /3)=((√(255))/4) ✓
$${we}\:{can}\:{easily}\:{get}\:{that}\:{the}\:{triangle}\:{A}'{B}'{C}' \\ $$$${with}\:{side}\:{lengthes}\:\mathrm{7},\:\mathrm{6}\:{and}\:\mathrm{4}\:{contains} \\ $$$${exactly}\:{the}\:{three}\:{hatched}\:{triangles}. \\ $$$$ \\ $$$${the}\:{area}\:{of}\:{triangle}\:{A}'{B}'{C}'\:{is} \\ $$$$\Delta_{{A}'{B}'{C}'} =\frac{\sqrt{\left(\mathrm{7}+\mathrm{6}+\mathrm{4}\right)\left(−\mathrm{7}+\mathrm{6}+\mathrm{4}\right)\left(\mathrm{7}−\mathrm{6}+\mathrm{4}\right)\left(\mathrm{7}+\mathrm{6}−\mathrm{4}\right)}}{\mathrm{4}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{17}×\mathrm{3}×\mathrm{5}×\mathrm{9}}}{\mathrm{4}}=\frac{\mathrm{3}\sqrt{\mathrm{255}}}{\mathrm{4}} \\ $$$${so}\:{the}\:{area}\:{of}\:{the}\:{shaded}\:{triangle}\:{is} \\ $$$$\Delta_{{ABC}'} =\frac{\Delta_{{A}'{B}'{C}'} }{\mathrm{3}}=\frac{\sqrt{\mathrm{255}}}{\mathrm{4}}\:\checkmark \\ $$
Commented by manxsol last updated on 17/Nov/22
Commented by mr W last updated on 17/Nov/22
thanks!
$${thanks}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *