Question Number 180813 by mr W last updated on 17/Nov/22
Commented by mr W last updated on 17/Nov/22
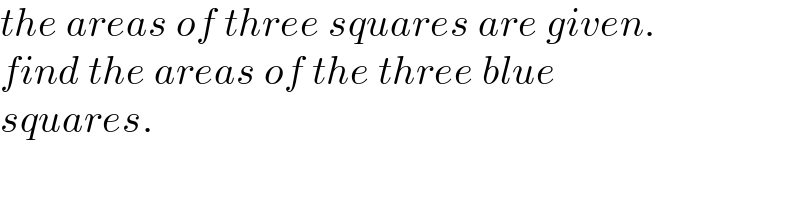
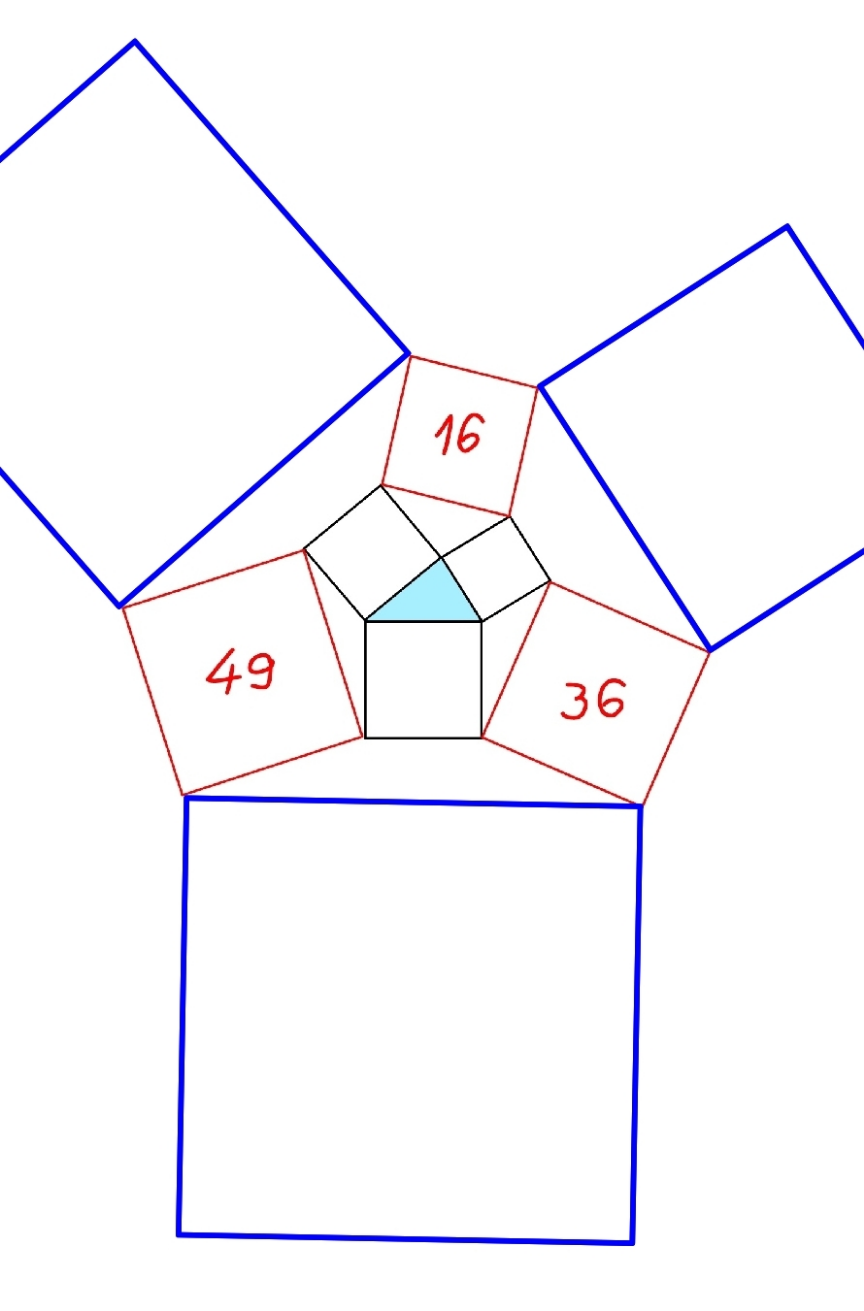
$${the}\:{areas}\:{of}\:{three}\:{squares}\:{are}\:{given}. \\ $$$${find}\:{the}\:{areas}\:{of}\:{the}\:{three}\:{blue}\: \\ $$$${squares}. \\ $$
Commented by a.lgnaoui last updated on 17/Nov/22
Commented by mr W last updated on 18/Nov/22

Commented by mr W last updated on 18/Nov/22
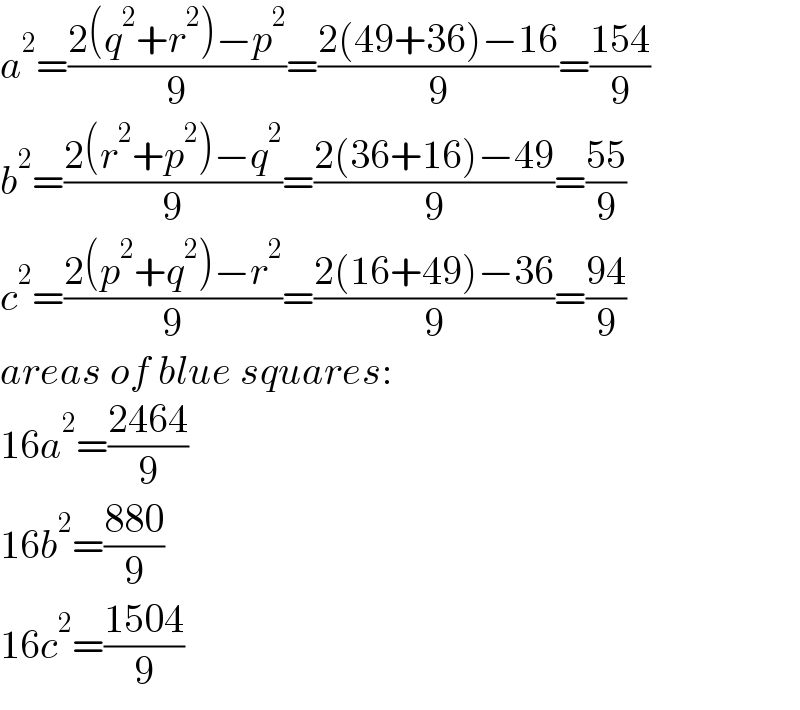
$${a}^{\mathrm{2}} =\frac{\mathrm{2}\left({q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right)−{p}^{\mathrm{2}} }{\mathrm{9}}=\frac{\mathrm{2}\left(\mathrm{49}+\mathrm{36}\right)−\mathrm{16}}{\mathrm{9}}=\frac{\mathrm{154}}{\mathrm{9}} \\ $$$${b}^{\mathrm{2}} =\frac{\mathrm{2}\left({r}^{\mathrm{2}} +{p}^{\mathrm{2}} \right)−{q}^{\mathrm{2}} }{\mathrm{9}}=\frac{\mathrm{2}\left(\mathrm{36}+\mathrm{16}\right)−\mathrm{49}}{\mathrm{9}}=\frac{\mathrm{55}}{\mathrm{9}} \\ $$$${c}^{\mathrm{2}} =\frac{\mathrm{2}\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} \right)−{r}^{\mathrm{2}} }{\mathrm{9}}=\frac{\mathrm{2}\left(\mathrm{16}+\mathrm{49}\right)−\mathrm{36}}{\mathrm{9}}=\frac{\mathrm{94}}{\mathrm{9}} \\ $$$${areas}\:{of}\:{blue}\:{squares}: \\ $$$$\mathrm{16}{a}^{\mathrm{2}} =\frac{\mathrm{2464}}{\mathrm{9}} \\ $$$$\mathrm{16}{b}^{\mathrm{2}} =\frac{\mathrm{880}}{\mathrm{9}} \\ $$$$\mathrm{16}{c}^{\mathrm{2}} =\frac{\mathrm{1504}}{\mathrm{9}} \\ $$
Commented by mr W last updated on 19/Nov/22

$${proof}\:{see}\:{Q}\mathrm{180882} \\ $$
Answered by a.lgnaoui last updated on 18/Nov/22
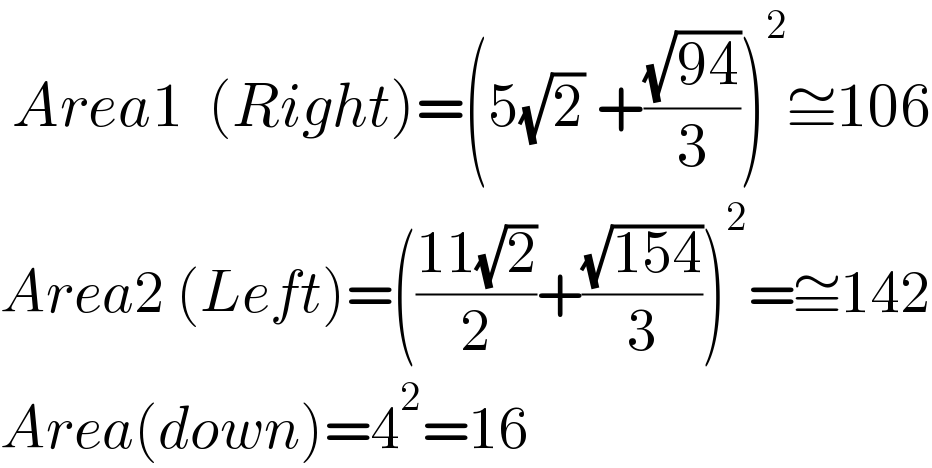
$$\:{Area}\mathrm{1}\:\:\left({Right}\right)=\left(\mathrm{5}\sqrt{\mathrm{2}}\:+\frac{\sqrt{\mathrm{94}}}{\mathrm{3}}\right)^{\mathrm{2}} \cong\mathrm{106} \\ $$$${Area}\mathrm{2}\:\left({Left}\right)=\left(\frac{\mathrm{11}\sqrt{\mathrm{2}}}{\mathrm{2}}+\frac{\sqrt{\mathrm{154}}}{\mathrm{3}}\right)^{\mathrm{2}} =\cong\mathrm{142} \\ $$$${Area}\left({down}\right)=\mathrm{4}^{\mathrm{2}} =\mathrm{16} \\ $$
Commented by a.lgnaoui last updated on 18/Nov/22
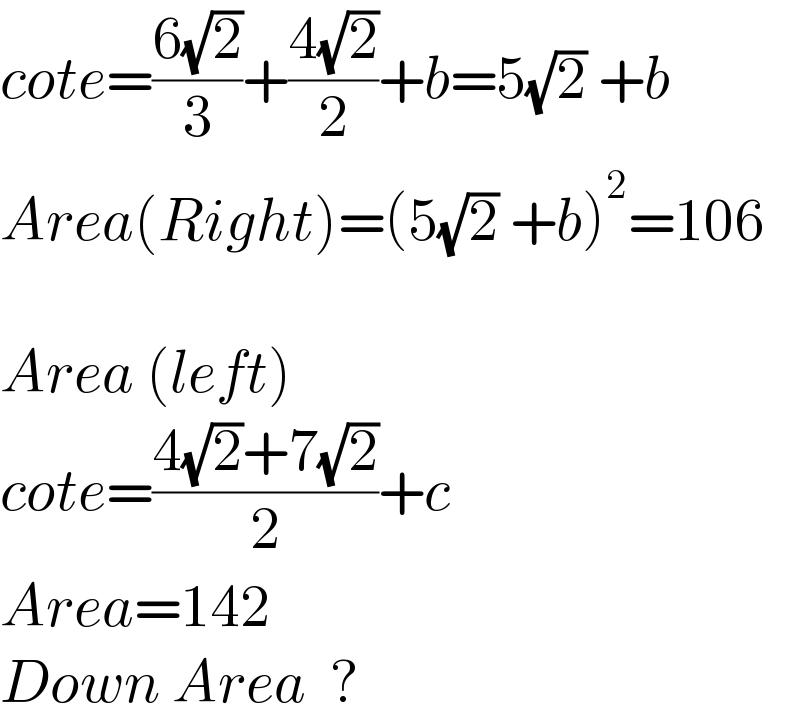
$${cote}=\frac{\mathrm{6}\sqrt{\mathrm{2}}}{\mathrm{3}}+\frac{\mathrm{4}\sqrt{\mathrm{2}}}{\mathrm{2}}+{b}=\mathrm{5}\sqrt{\mathrm{2}}\:+{b} \\ $$$${Area}\left({Right}\right)=\left(\mathrm{5}\sqrt{\mathrm{2}}\:+{b}\right)^{\mathrm{2}} =\mathrm{106} \\ $$$$ \\ $$$${Area}\:\left({left}\right) \\ $$$${cote}=\frac{\mathrm{4}\sqrt{\mathrm{2}}+\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{2}}+{c} \\ $$$${Area}=\mathrm{142} \\ $$$${Down}\:{Area}\:\:? \\ $$
