Question Number 180897 by depressiveshrek last updated on 18/Nov/22

Commented by depressiveshrek last updated on 18/Nov/22

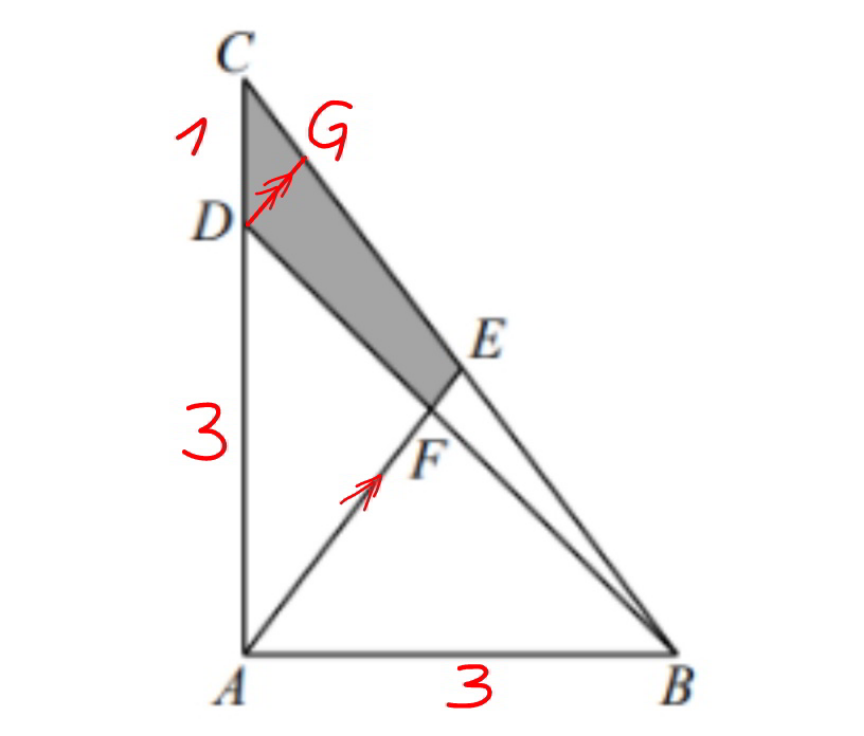
$$\mid{AB}\mid=\mathrm{3} \\ $$$$\mid{BC}\mid=\mathrm{5} \\ $$$${BE}={EC} \\ $$$$\mid{CD}\mid=\mathrm{1} \\ $$$${Find}\:{the}\:{area}\:{of}\:{the}\:{white}\:\left({not}\:{the}\:{gray}\:{one}\right)\:{area} \\ $$
Commented by manxsol last updated on 19/Nov/22

Commented by mr W last updated on 19/Nov/22
$${fine}! \\ $$$${but}\:{please}\:{post}\:{answer}\:{as}\:“{answer}'', \\ $$$${not}\:{as}\:“{comment}''! \\ $$
Commented by manxsol last updated on 19/Nov/22
$${it}\:{is}\:{understood}\:{Sr}.{W},\:{excuse}\:{me} \\ $$
Commented by mr W last updated on 19/Nov/22

$${thanks}\:{alot}! \\ $$
Answered by mr W last updated on 19/Nov/22
Commented by mr W last updated on 19/Nov/22
![AC=(√(5^2 −3^2 ))=4 AE=BE=(5/2) DG=(1/4)×AE=(5/8) CG=(1/4)×CE=(1/4)×(5/2)=(5/8) ((DF)/(DB))=((GE)/(GB))=(((5/2)−(5/8))/(5−(5/8)))=(3/7) [ΔAEB]=(([ΔABC])/2)=((3×4)/(2×2))=3 [ΔADB]=((3×3)/2)=(9/2) [ΔADF]=(3/7)×[ADB]=((27)/(14)) white area=((27)/(14))+3=((69)/(14))](https://www.tinkutara.com/question/Q180913.png)
$${AC}=\sqrt{\mathrm{5}^{\mathrm{2}} −\mathrm{3}^{\mathrm{2}} }=\mathrm{4} \\ $$$${AE}={BE}=\frac{\mathrm{5}}{\mathrm{2}} \\ $$$${DG}=\frac{\mathrm{1}}{\mathrm{4}}×{AE}=\frac{\mathrm{5}}{\mathrm{8}} \\ $$$${CG}=\frac{\mathrm{1}}{\mathrm{4}}×{CE}=\frac{\mathrm{1}}{\mathrm{4}}×\frac{\mathrm{5}}{\mathrm{2}}=\frac{\mathrm{5}}{\mathrm{8}} \\ $$$$\frac{{DF}}{{DB}}=\frac{{GE}}{{GB}}=\frac{\frac{\mathrm{5}}{\mathrm{2}}−\frac{\mathrm{5}}{\mathrm{8}}}{\mathrm{5}−\frac{\mathrm{5}}{\mathrm{8}}}=\frac{\mathrm{3}}{\mathrm{7}} \\ $$$$\left[\Delta{AEB}\right]=\frac{\left[\Delta{ABC}\right]}{\mathrm{2}}=\frac{\mathrm{3}×\mathrm{4}}{\mathrm{2}×\mathrm{2}}=\mathrm{3} \\ $$$$\left[\Delta{ADB}\right]=\frac{\mathrm{3}×\mathrm{3}}{\mathrm{2}}=\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\left[\Delta{ADF}\right]=\frac{\mathrm{3}}{\mathrm{7}}×\left[{ADB}\right]=\frac{\mathrm{27}}{\mathrm{14}} \\ $$$${white}\:{area}=\frac{\mathrm{27}}{\mathrm{14}}+\mathrm{3}=\frac{\mathrm{69}}{\mathrm{14}} \\ $$
Commented by mr W last updated on 19/Nov/22
![alternative: A(0,0) E((3/2),2) D(0,3) eqn. of AE: y=((4x)/3) eqn. of BD: y=3−x intersection point F: y=((4x)/3)=3−x ⇒x=(9/7), y=((12)/7) [ΔAEB]=((2×3)/2)=3 [ΔADF]=(3/2)×(9/7)=((27)/(14)) white area=3+((27)/(14))=((69)/(14)) ✓](https://www.tinkutara.com/question/Q180914.png)
$${alternative}: \\ $$$${A}\left(\mathrm{0},\mathrm{0}\right) \\ $$$${E}\left(\frac{\mathrm{3}}{\mathrm{2}},\mathrm{2}\right) \\ $$$${D}\left(\mathrm{0},\mathrm{3}\right) \\ $$$${eqn}.\:{of}\:{AE}: \\ $$$${y}=\frac{\mathrm{4}{x}}{\mathrm{3}} \\ $$$${eqn}.\:{of}\:{BD}: \\ $$$${y}=\mathrm{3}−{x} \\ $$$${intersection}\:{point}\:{F}: \\ $$$${y}=\frac{\mathrm{4}{x}}{\mathrm{3}}=\mathrm{3}−{x} \\ $$$$\Rightarrow{x}=\frac{\mathrm{9}}{\mathrm{7}},\:{y}=\frac{\mathrm{12}}{\mathrm{7}} \\ $$$$\left[\Delta{AEB}\right]=\frac{\mathrm{2}×\mathrm{3}}{\mathrm{2}}=\mathrm{3} \\ $$$$\left[\Delta{ADF}\right]=\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{9}}{\mathrm{7}}=\frac{\mathrm{27}}{\mathrm{14}} \\ $$$${white}\:{area}=\mathrm{3}+\frac{\mathrm{27}}{\mathrm{14}}=\frac{\mathrm{69}}{\mathrm{14}}\:\checkmark \\ $$
