Question Number 180998 by HeferH last updated on 20/Nov/22
Answered by mr W last updated on 20/Nov/22
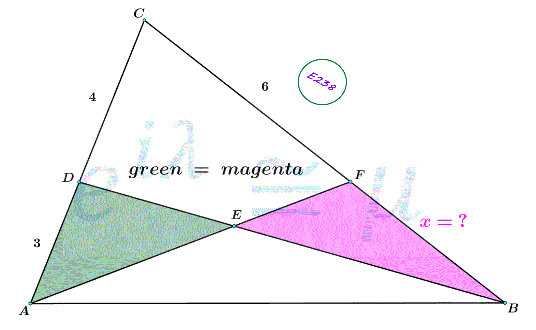
![[ΔADB]=[ΔAEB]+green =[ΔAEB]+magenta =[ΔAFB] ⇒DF//AB ⇒(4/3)=(6/x) ⇒x=((3×6)/4)=(9/2)=4.5](https://www.tinkutara.com/question/Q181004.png)
$$\left[\Delta{ADB}\right]=\left[\Delta{AEB}\right]+{green} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left[\Delta{AEB}\right]+{magenta} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\left[\Delta{AFB}\right] \\ $$$$\Rightarrow{DF}//{AB} \\ $$$$\Rightarrow\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{6}}{{x}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{3}×\mathrm{6}}{\mathrm{4}}=\frac{\mathrm{9}}{\mathrm{2}}=\mathrm{4}.\mathrm{5} \\ $$
Answered by mnjuly1970 last updated on 20/Nov/22
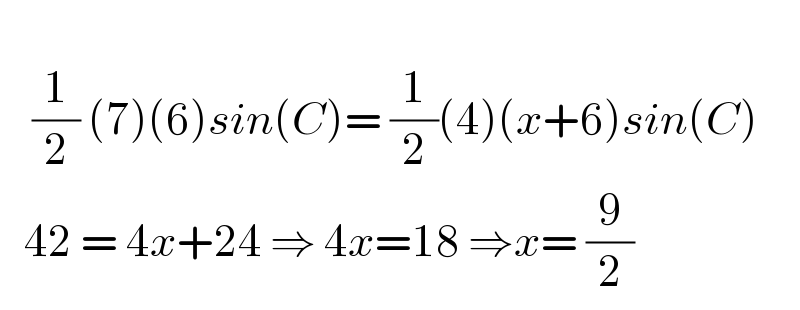
$$\:\: \\ $$$$\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\left(\mathrm{7}\right)\left(\mathrm{6}\right){sin}\left({C}\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{4}\right)\left({x}+\mathrm{6}\right){sin}\left({C}\right) \\ $$$$\:\:\:\mathrm{42}\:=\:\mathrm{4}{x}+\mathrm{24}\:\Rightarrow\:\mathrm{4}{x}=\mathrm{18}\:\Rightarrow{x}=\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$
