Question Number 181085 by mr W last updated on 21/Nov/22

Commented by mr W last updated on 21/Nov/22
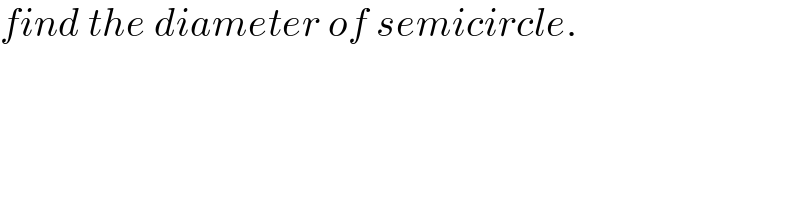
$${find}\:{the}\:{diameter}\:{of}\:{semicircle}. \\ $$
Commented by HeferH last updated on 21/Nov/22

$${R}\:=\:\mathrm{12}.\mathrm{5}? \\ $$
Commented by mr W last updated on 21/Nov/22

$${yes}! \\ $$
Answered by mr W last updated on 21/Nov/22

Commented by mr W last updated on 21/Nov/22

$${r}_{\mathrm{1}} +{r}_{\mathrm{2}} =\sqrt{\left({R}−{r}_{\mathrm{1}} \right)^{\mathrm{2}} −{r}_{\mathrm{1}} ^{\mathrm{2}} }+\sqrt{\left({R}−{r}_{\mathrm{2}} \right)^{\mathrm{2}} −{r}_{\mathrm{2}} ^{\mathrm{2}} } \\ $$$$\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)−\sqrt{{R}\left({R}−\mathrm{2}{r}_{\mathrm{1}} \right)}=\sqrt{{R}\left({R}−\mathrm{2}{r}_{\mathrm{2}} \right)} \\ $$$$\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{2}{R}\left({r}_{\mathrm{1}} −{r}_{\mathrm{2}} \right)=\mathrm{2}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)\sqrt{{R}\left({R}−\mathrm{2}{r}_{\mathrm{1}} \right)} \\ $$$$\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{4}} −\mathrm{4}{R}\left({r}_{\mathrm{1}} −{r}_{\mathrm{2}} \right)\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{R}^{\mathrm{2}} \left({r}_{\mathrm{1}} −{r}_{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{4}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{2}} {R}\left({R}−\mathrm{2}{r}_{\mathrm{1}} \right) \\ $$$$\mathrm{4}{r}_{\mathrm{1}} {r}_{\mathrm{2}} \left(\mathrm{2}{R}\right)^{\mathrm{2}} −\mathrm{2}\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{3}} \left(\mathrm{2}{R}\right)−\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{4}} =\mathrm{0} \\ $$$$\Rightarrow\mathrm{2}{R}=\frac{\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{2}} \left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} +\sqrt{\left({r}_{\mathrm{1}} +{r}_{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{r}_{\mathrm{1}} {r}_{\mathrm{2}} }\right)}{\mathrm{4}{r}_{\mathrm{1}} {r}_{\mathrm{2}} } \\ $$$$\Rightarrow\mathrm{2}{R}=\frac{\mathrm{10}^{\mathrm{2}} \left(\mathrm{10}+\sqrt{\mathrm{10}^{\mathrm{2}} +\mathrm{4}×\mathrm{24}}\right)}{\mathrm{4}×\mathrm{24}}=\mathrm{25}\:\checkmark \\ $$
