Question Number 181153 by cortano1 last updated on 22/Nov/22

Answered by Acem last updated on 22/Nov/22
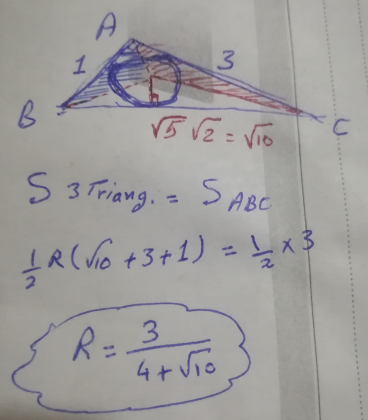
Commented by Acem last updated on 22/Nov/22

$${I}\:{got}\:{the}\:{question}\:{as}\:{wrong},\:{hope}\:{my}\:{English}'{s} \\ $$$$\:{getting}\:{better}. \\ $$
Answered by mr W last updated on 22/Nov/22
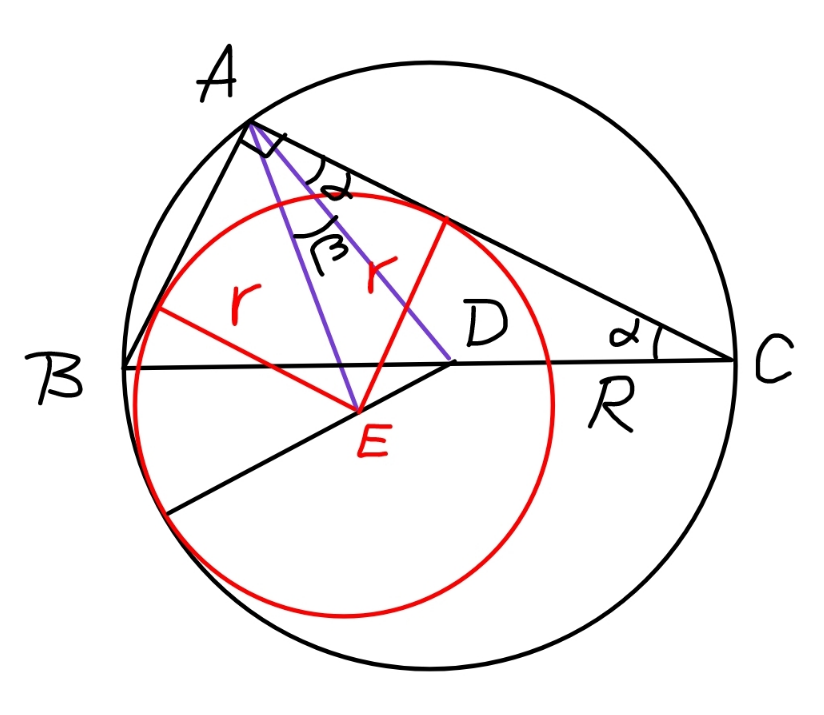
Commented by Acem last updated on 22/Nov/22
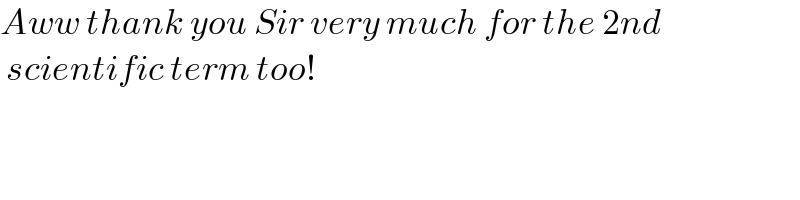
$${Aww}\:{thank}\:{you}\:{Sir}\:{very}\:{much}\:{for}\:{the}\:\mathrm{2}{nd} \\ $$$$\:{scientific}\:{term}\:{too}! \\ $$
Commented by mr W last updated on 22/Nov/22
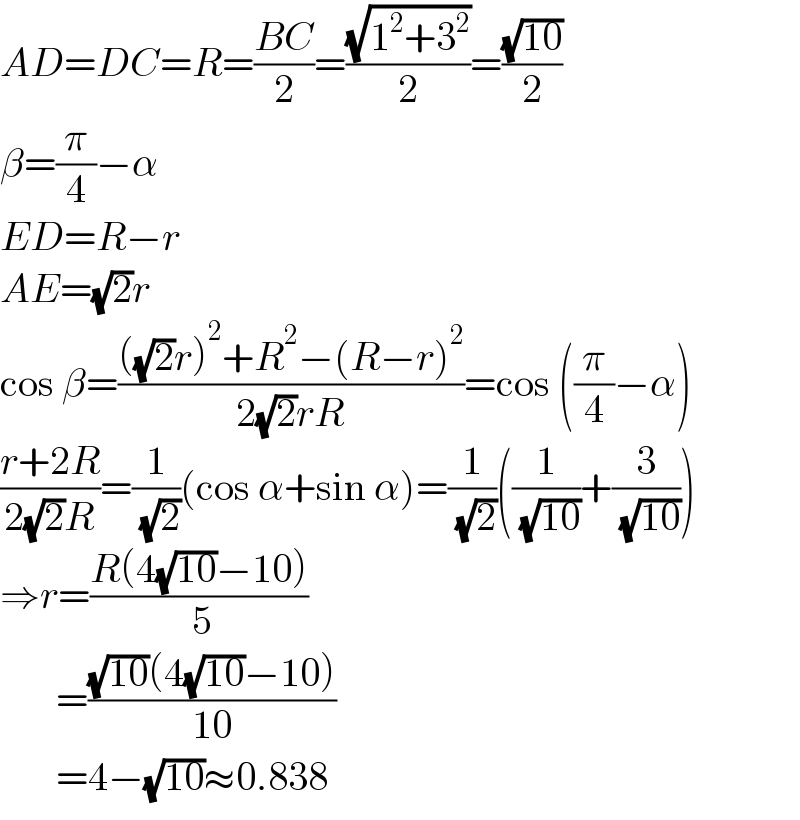
$${AD}={DC}={R}=\frac{{BC}}{\mathrm{2}}=\frac{\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{3}^{\mathrm{2}} }}{\mathrm{2}}=\frac{\sqrt{\mathrm{10}}}{\mathrm{2}} \\ $$$$\beta=\frac{\pi}{\mathrm{4}}−\alpha \\ $$$${ED}={R}−{r} \\ $$$${AE}=\sqrt{\mathrm{2}}{r} \\ $$$$\mathrm{cos}\:\beta=\frac{\left(\sqrt{\mathrm{2}}{r}\right)^{\mathrm{2}} +{R}^{\mathrm{2}} −\left({R}−{r}\right)^{\mathrm{2}} }{\mathrm{2}\sqrt{\mathrm{2}}{rR}}=\mathrm{cos}\:\left(\frac{\pi}{\mathrm{4}}−\alpha\right) \\ $$$$\frac{{r}+\mathrm{2}{R}}{\mathrm{2}\sqrt{\mathrm{2}}{R}}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\mathrm{cos}\:\alpha+\mathrm{sin}\:\alpha\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{10}}}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{10}}}\right) \\ $$$$\Rightarrow{r}=\frac{{R}\left(\mathrm{4}\sqrt{\mathrm{10}}−\mathrm{10}\right)}{\:\mathrm{5}} \\ $$$$\:\:\:\:\:\:\:=\frac{\sqrt{\mathrm{10}}\left(\mathrm{4}\sqrt{\mathrm{10}}−\mathrm{10}\right)}{\mathrm{10}} \\ $$$$\:\:\:\:\:\:\:=\mathrm{4}−\sqrt{\mathrm{10}}\approx\mathrm{0}.\mathrm{838} \\ $$
Commented by Acem last updated on 22/Nov/22
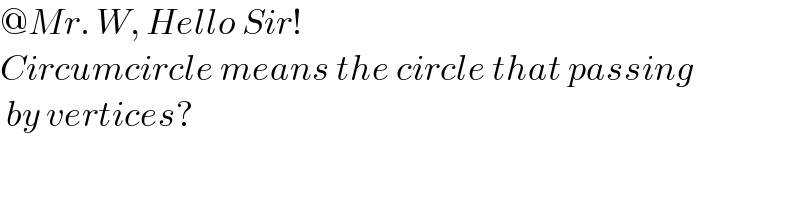
$$@{Mr}.\:{W},\:{Hello}\:{Sir}! \\ $$$${Circumcircle}\:{means}\:{the}\:{circle}\:{that}\:{passing} \\ $$$$\:{by}\:{vertices}? \\ $$
Commented by mr W last updated on 22/Nov/22

$${yes},\:{sir}. \\ $$
Commented by mr W last updated on 22/Nov/22
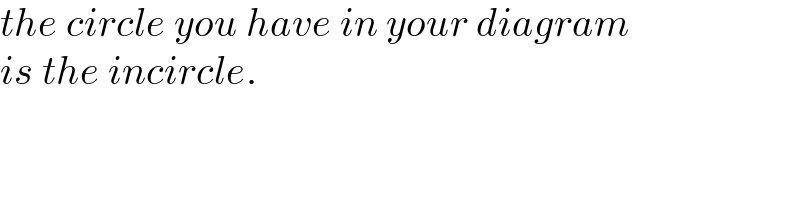
$${the}\:{circle}\:{you}\:{have}\:{in}\:{your}\:{diagram} \\ $$$${is}\:{the}\:{incircle}.\: \\ $$
