Question Number 181217 by Mastermind last updated on 23/Nov/22

Answered by Rasheed.Sindhi last updated on 23/Nov/22
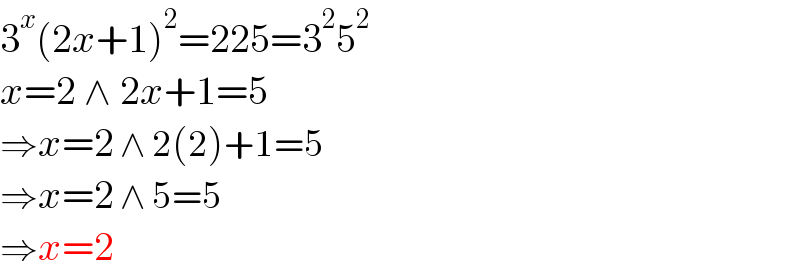
$$\mathrm{3}^{{x}} \left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{225}=\mathrm{3}^{\mathrm{2}} \mathrm{5}^{\mathrm{2}} \\ $$$${x}=\mathrm{2}\:\wedge\:\mathrm{2}{x}+\mathrm{1}=\mathrm{5} \\ $$$$\Rightarrow{x}=\mathrm{2}\:\wedge\:\mathrm{2}\left(\mathrm{2}\right)+\mathrm{1}=\mathrm{5} \\ $$$$\Rightarrow{x}=\mathrm{2}\:\wedge\:\mathrm{5}=\mathrm{5} \\ $$$$\Rightarrow{x}=\mathrm{2}\: \\ $$
Commented by mr W last updated on 23/Nov/22
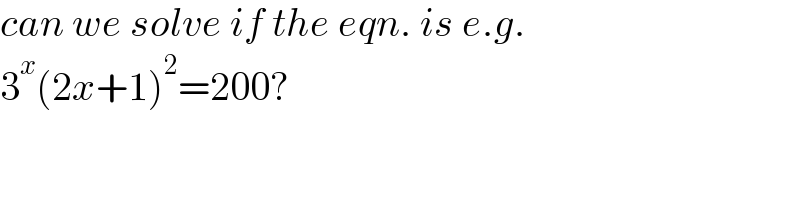
$${can}\:{we}\:{solve}\:{if}\:{the}\:{eqn}.\:{is}\:{e}.{g}. \\ $$$$\mathrm{3}^{{x}} \left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{200}? \\ $$
Commented by Rasheed.Sindhi last updated on 23/Nov/22
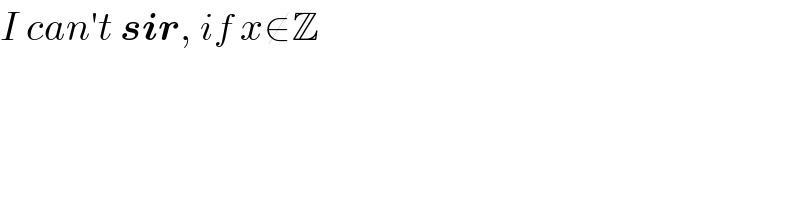
$${I}\:{can}'{t}\:\boldsymbol{{sir}},\:{if}\:{x}\notin\mathbb{Z} \\ $$
Commented by mr W last updated on 23/Nov/22
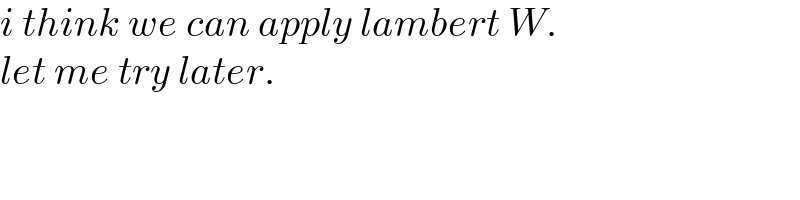
$${i}\:{think}\:{we}\:{can}\:{apply}\:{lambert}\:{W}. \\ $$$${let}\:{me}\:{try}\:{later}. \\ $$
Commented by mr W last updated on 23/Nov/22
![3^x (2x+1)^2 =200 3^x =(((√(200))/(2x+1)))^2 3^(x/2) =((√(200))/(4((x/2)+(1/4)))) 3^((x/2)+(1/4)) =((√(200(√3)))/(4((x/2)+(1/4)))) ((x/2)+(1/4))ln 3 e^(((x/2)+(1/4))ln 3) =(((ln 3 )(√(200(√3))))/4) ⇒x=(2/(ln 3))W[(((ln 3 )(√(200(√3))))/4)]−(1/2) ≈((2×1.3393676)/(ln 3))−(1/2)=1.93829](https://www.tinkutara.com/question/Q181242.png)
$$\mathrm{3}^{{x}} \left(\mathrm{2}{x}+\mathrm{1}\right)^{\mathrm{2}} =\mathrm{200} \\ $$$$\mathrm{3}^{{x}} =\left(\frac{\sqrt{\mathrm{200}}}{\mathrm{2}{x}+\mathrm{1}}\right)^{\mathrm{2}} \\ $$$$\mathrm{3}^{\frac{{x}}{\mathrm{2}}} =\frac{\sqrt{\mathrm{200}}}{\mathrm{4}\left(\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)} \\ $$$$\mathrm{3}^{\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}} =\frac{\sqrt{\mathrm{200}\sqrt{\mathrm{3}}}}{\mathrm{4}\left(\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)} \\ $$$$\left(\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\mathrm{ln}\:\mathrm{3}\:{e}^{\left(\frac{{x}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{4}}\right)\mathrm{ln}\:\mathrm{3}} =\frac{\left(\mathrm{ln}\:\mathrm{3}\:\right)\sqrt{\mathrm{200}\sqrt{\mathrm{3}}}}{\mathrm{4}} \\ $$$$\Rightarrow{x}=\frac{\mathrm{2}}{\mathrm{ln}\:\mathrm{3}}{W}\left[\frac{\left(\mathrm{ln}\:\mathrm{3}\:\right)\sqrt{\mathrm{200}\sqrt{\mathrm{3}}}}{\mathrm{4}}\right]−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\approx\frac{\mathrm{2}×\mathrm{1}.\mathrm{3393676}}{\mathrm{ln}\:\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{1}.\mathrm{93829} \\ $$
