Menu Close

Question-181279

Tinku Tara 0 Comments
Pin




Question Number 181279 by mnjuly1970 last updated on 23/Nov/22
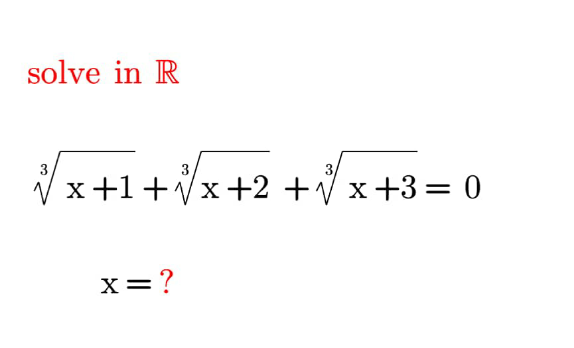
Answered by Rasheed.Sindhi last updated on 25/Nov/22
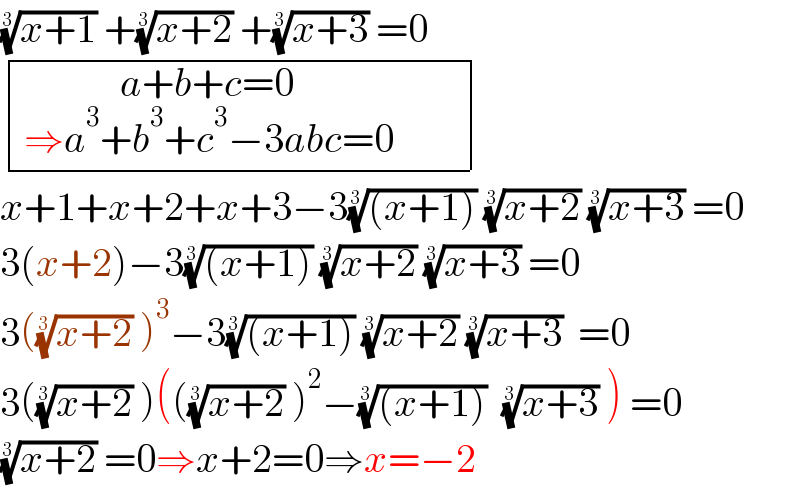
((x+1))^(1/3) +((x+2))^(1/3) +((x+3))^(1/3) =0 determinant (((a+b+c=0_( ⇒a^3 +b^3 +c^3 −3abc=0) ))) x+1+x+2+x+3−3(((x+1)))^(1/3) ((x+2))^(1/3) ((x+3))^(1/3) =0 3(x+2)−3(((x+1)))^(1/3) ((x+2))^(1/3) ((x+3))^(1/3) =0 3(((x+2))^(1/3) )^3 −3(((x+1)))^(1/3) ((x+2))^(1/3) ((x+3))^(1/3) =0 3(((x+2))^(1/3) )((((x+2))^(1/3) )^2 −(((x+1)))^(1/3) ((x+3))^(1/3) ) =0 ((x+2))^(1/3) =0⇒x+2=0⇒x=−2
$$\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}\:+\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:+\sqrt[{\mathrm{3}}]{{x}+\mathrm{3}}\:=\mathrm{0} \\ $$$$\begin{array}{|c|}{\underset{\:\Rightarrow{a}^{\mathrm{3}} +{b}^{\mathrm{3}} +{c}^{\mathrm{3}} −\mathrm{3}{abc}=\mathrm{0}} {{a}+{b}+{c}=\mathrm{0}}\:\:\:\:\:\:\:\:}\\\hline\end{array} \\ $$$${x}+\mathrm{1}+{x}+\mathrm{2}+{x}+\mathrm{3}−\mathrm{3}\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)}\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{3}}\:=\mathrm{0} \\ $$$$\mathrm{3}\left({x}+\mathrm{2}\right)−\mathrm{3}\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)}\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{3}}\:=\mathrm{0} \\ $$$$\mathrm{3}\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:\right)^{\mathrm{3}} −\mathrm{3}\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)}\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{3}}\:\:=\mathrm{0} \\ $$$$\mathrm{3}\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:\right)\left(\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:\right)^{\mathrm{2}} −\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)}\:\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{3}}\:\right)\:=\mathrm{0} \\ $$$$\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:=\mathrm{0}\Rightarrow{x}+\mathrm{2}=\mathrm{0}\Rightarrow{x}=−\mathrm{2} \\ $$
Answered by Rasheed.Sindhi last updated on 23/Nov/22
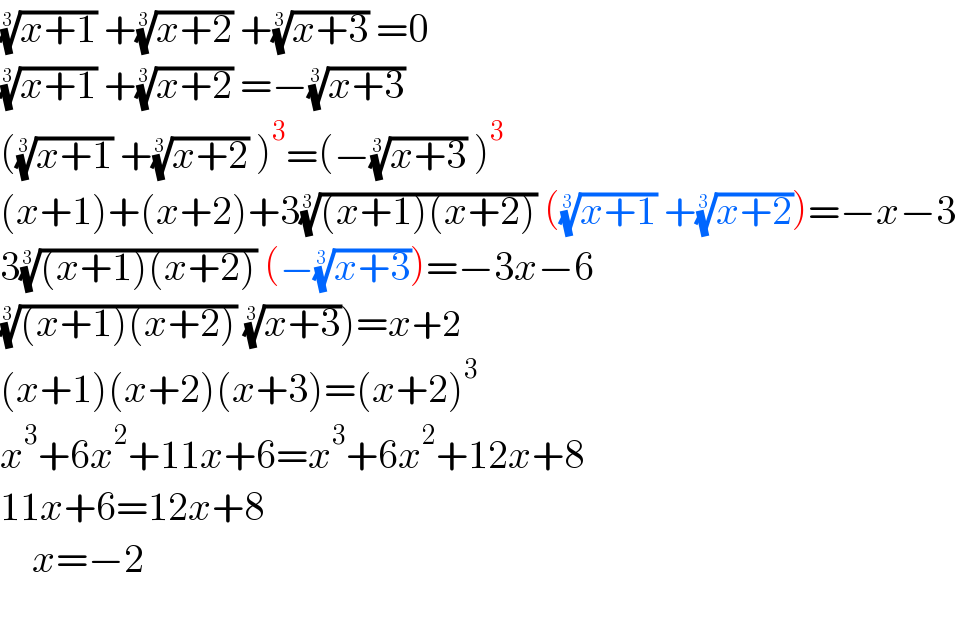
((x+1))^(1/3) +((x+2))^(1/3) +((x+3))^(1/3) =0 ((x+1))^(1/3) +((x+2))^(1/3) =−((x+3))^(1/3) (((x+1))^(1/3) +((x+2))^(1/3) )^3 =(−((x+3))^(1/3) )^3 (x+1)+(x+2)+3(((x+1)(x+2)))^(1/3) (((x+1))^(1/3) +((x+2))^(1/3) )=−x−3 3(((x+1)(x+2)))^(1/3) (−((x+3))^(1/3) )=−3x−6 (((x+1)(x+2)))^(1/3) ((x+3))^(1/3) )=x+2 (x+1)(x+2)(x+3)=(x+2)^3 x^3 +6x^2 +11x+6=x^3 +6x^2 +12x+8 11x+6=12x+8 x=−2
$$\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}\:+\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:+\sqrt[{\mathrm{3}}]{{x}+\mathrm{3}}\:=\mathrm{0} \\ $$$$\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}\:+\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:=−\sqrt[{\mathrm{3}}]{{x}+\mathrm{3}}\: \\ $$$$\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}\:+\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\:\right)^{\mathrm{3}} =\left(−\sqrt[{\mathrm{3}}]{{x}+\mathrm{3}}\:\right)^{\mathrm{3}} \\ $$$$\left({x}+\mathrm{1}\right)+\left({x}+\mathrm{2}\right)+\mathrm{3}\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}\:\left(\sqrt[{\mathrm{3}}]{{x}+\mathrm{1}}\:+\sqrt[{\mathrm{3}}]{{x}+\mathrm{2}}\right)=−{x}−\mathrm{3} \\ $$$$\mathrm{3}\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}\:\left(−\sqrt[{\mathrm{3}}]{{x}+\mathrm{3}}\right)=−\mathrm{3}{x}−\mathrm{6} \\ $$$$\left.\sqrt[{\mathrm{3}}]{\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)}\:\sqrt[{\mathrm{3}}]{{x}+\mathrm{3}}\right)={x}+\mathrm{2} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)=\left({x}+\mathrm{2}\right)^{\mathrm{3}} \\ $$$${x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{11}{x}+\mathrm{6}={x}^{\mathrm{3}} +\mathrm{6}{x}^{\mathrm{2}} +\mathrm{12}{x}+\mathrm{8} \\ $$$$\mathrm{11}{x}+\mathrm{6}=\mathrm{12}{x}+\mathrm{8} \\ $$$$\:\:\:\:{x}=−\mathrm{2} \\ $$$$ \\ $$
Commented by Frix last updated on 23/Nov/22
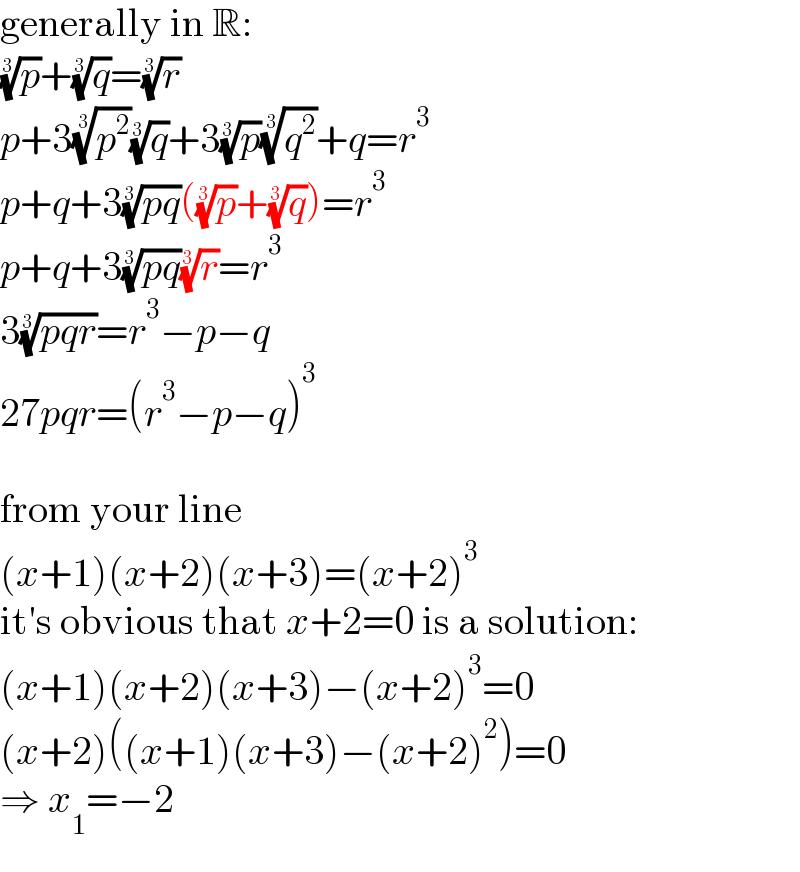
generally in R: (p)^(1/3) +(q)^(1/3) =(r)^(1/3) p+3(p^2 )^(1/3) (q)^(1/3) +3(p)^(1/3) (q^2 )^(1/3) +q=r^3 p+q+3((pq))^(1/3) ((p)^(1/3) +(q)^(1/3) )=r^3 p+q+3((pq))^(1/3) (r)^(1/3) =r^3 3((pqr))^(1/3) =r^3 −p−q 27pqr=(r^3 −p−q)^3 from your line (x+1)(x+2)(x+3)=(x+2)^3 it′s obvious that x+2=0 is a solution: (x+1)(x+2)(x+3)−(x+2)^3 =0 (x+2)((x+1)(x+3)−(x+2)^2 )=0 ⇒ x_1 =−2
$$\mathrm{generally}\:\mathrm{in}\:\mathbb{R}: \\ $$$$\sqrt[{\mathrm{3}}]{{p}}+\sqrt[{\mathrm{3}}]{{q}}=\sqrt[{\mathrm{3}}]{{r}} \\ $$$${p}+\mathrm{3}\sqrt[{\mathrm{3}}]{{p}^{\mathrm{2}} }\sqrt[{\mathrm{3}}]{{q}}+\mathrm{3}\sqrt[{\mathrm{3}}]{{p}}\sqrt[{\mathrm{3}}]{{q}^{\mathrm{2}} }+{q}={r}^{\mathrm{3}} \\ $$$${p}+{q}+\mathrm{3}\sqrt[{\mathrm{3}}]{{pq}}\left(\sqrt[{\mathrm{3}}]{{p}}+\sqrt[{\mathrm{3}}]{{q}}\right)={r}^{\mathrm{3}} \\ $$$${p}+{q}+\mathrm{3}\sqrt[{\mathrm{3}}]{{pq}}\sqrt[{\mathrm{3}}]{{r}}={r}^{\mathrm{3}} \\ $$$$\mathrm{3}\sqrt[{\mathrm{3}}]{{pqr}}={r}^{\mathrm{3}} −{p}−{q} \\ $$$$\mathrm{27}{pqr}=\left({r}^{\mathrm{3}} −{p}−{q}\right)^{\mathrm{3}} \\ $$$$ \\ $$$$\mathrm{from}\:\mathrm{your}\:\mathrm{line} \\ $$$$\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)=\left({x}+\mathrm{2}\right)^{\mathrm{3}} \\ $$$$\mathrm{it}'\mathrm{s}\:\mathrm{obvious}\:\mathrm{that}\:{x}+\mathrm{2}=\mathrm{0}\:\mathrm{is}\:\mathrm{a}\:\mathrm{solution}: \\ $$$$\left({x}+\mathrm{1}\right)\left({x}+\mathrm{2}\right)\left({x}+\mathrm{3}\right)−\left({x}+\mathrm{2}\right)^{\mathrm{3}} =\mathrm{0} \\ $$$$\left({x}+\mathrm{2}\right)\left(\left({x}+\mathrm{1}\right)\left({x}+\mathrm{3}\right)−\left({x}+\mathrm{2}\right)^{\mathrm{2}} \right)=\mathrm{0} \\ $$$$\Rightarrow\:{x}_{\mathrm{1}} =−\mathrm{2} \\ $$
Commented by Rasheed.Sindhi last updated on 23/Nov/22
Thanks sir FrΠ^(⧫) x!
$$\mathbb{T}\mathrm{hanks}\:\mathrm{sir}\:\mathbb{F}\mathrm{r}\overset{\blacklozenge} {\Pi}\mathrm{x}! \\ $$
Answered by Frix last updated on 23/Nov/22
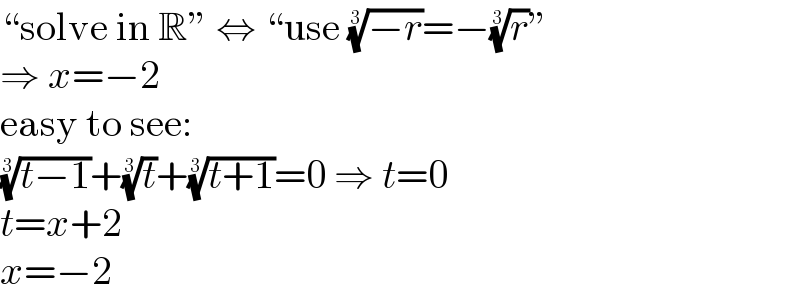
“solve in R” ⇔ “use ((−r))^(1/3) =−(r)^(1/3) ” ⇒ x=−2 easy to see: ((t−1))^(1/3) +(t)^(1/3) +((t+1))^(1/3) =0 ⇒ t=0 t=x+2 x=−2
$$“\mathrm{solve}\:\mathrm{in}\:\mathbb{R}''\:\Leftrightarrow\:“\mathrm{use}\:\sqrt[{\mathrm{3}}]{−{r}}=−\sqrt[{\mathrm{3}}]{{r}}'' \\ $$$$\Rightarrow\:{x}=−\mathrm{2} \\ $$$$\mathrm{easy}\:\mathrm{to}\:\mathrm{see}: \\ $$$$\sqrt[{\mathrm{3}}]{{t}−\mathrm{1}}+\sqrt[{\mathrm{3}}]{{t}}+\sqrt[{\mathrm{3}}]{{t}+\mathrm{1}}=\mathrm{0}\:\Rightarrow\:{t}=\mathrm{0} \\ $$$${t}={x}+\mathrm{2} \\ $$$${x}=−\mathrm{2} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *