Question Number 181329 by manxsol last updated on 24/Nov/22

Answered by som(math1967) last updated on 24/Nov/22

Commented by som(math1967) last updated on 24/Nov/22
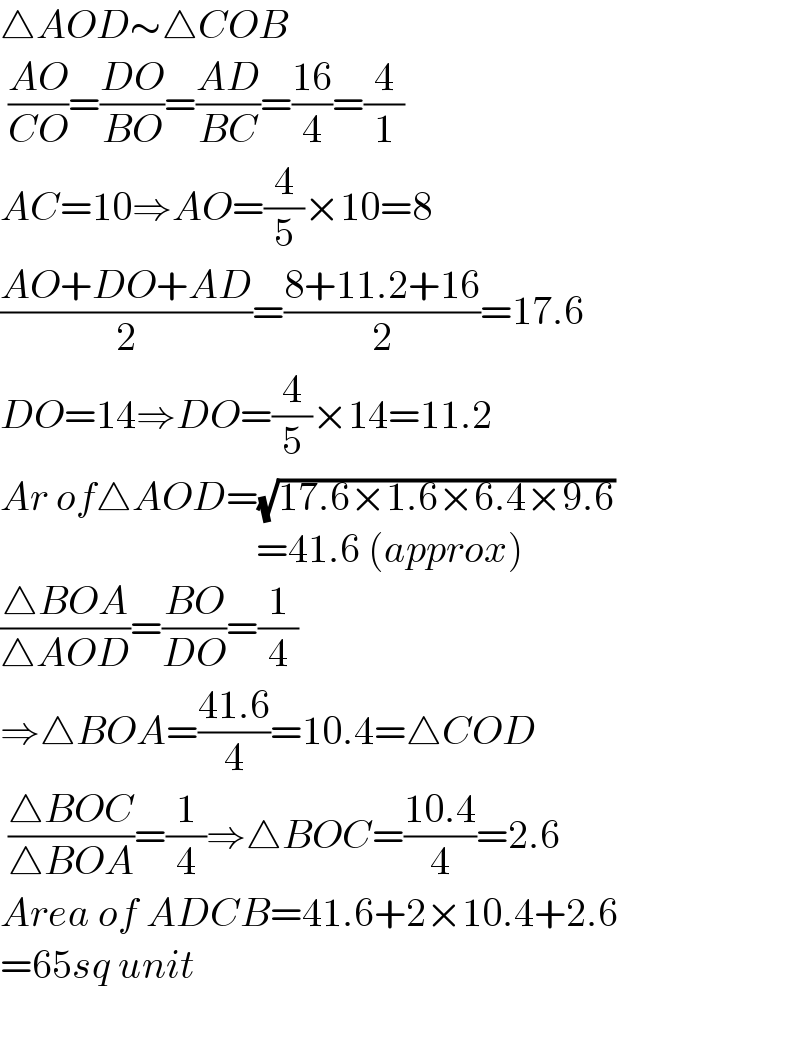
$$\bigtriangleup{AOD}\sim\bigtriangleup{COB} \\ $$$$\:\frac{{AO}}{{CO}}=\frac{{DO}}{{BO}}=\frac{{AD}}{{BC}}=\frac{\mathrm{16}}{\mathrm{4}}=\frac{\mathrm{4}}{\mathrm{1}} \\ $$$${AC}=\mathrm{10}\Rightarrow{AO}=\frac{\mathrm{4}}{\mathrm{5}}×\mathrm{10}=\mathrm{8} \\ $$$$\frac{{AO}+{DO}+{AD}}{\mathrm{2}}=\frac{\mathrm{8}+\mathrm{11}.\mathrm{2}+\mathrm{16}}{\mathrm{2}}=\mathrm{17}.\mathrm{6} \\ $$$${DO}=\mathrm{14}\Rightarrow{DO}=\frac{\mathrm{4}}{\mathrm{5}}×\mathrm{14}=\mathrm{11}.\mathrm{2} \\ $$$${Ar}\:{of}\bigtriangleup{AOD}=\sqrt{\mathrm{17}.\mathrm{6}×\mathrm{1}.\mathrm{6}×\mathrm{6}.\mathrm{4}×\mathrm{9}.\mathrm{6}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{41}.\mathrm{6}\:\left({approx}\right) \\ $$$$\frac{\bigtriangleup{BOA}}{\bigtriangleup{AOD}}=\frac{{BO}}{{DO}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\bigtriangleup{BOA}=\frac{\mathrm{41}.\mathrm{6}}{\mathrm{4}}=\mathrm{10}.\mathrm{4}=\bigtriangleup{COD} \\ $$$$\:\frac{\bigtriangleup{BOC}}{\bigtriangleup{BOA}}=\frac{\mathrm{1}}{\mathrm{4}}\Rightarrow\bigtriangleup{BOC}=\frac{\mathrm{10}.\mathrm{4}}{\mathrm{4}}=\mathrm{2}.\mathrm{6} \\ $$$${Area}\:{of}\:{ADCB}=\mathrm{41}.\mathrm{6}+\mathrm{2}×\mathrm{10}.\mathrm{4}+\mathrm{2}.\mathrm{6} \\ $$$$=\mathrm{65}{sq}\:{unit} \\ $$$$ \\ $$
Commented by manxsol last updated on 24/Nov/22
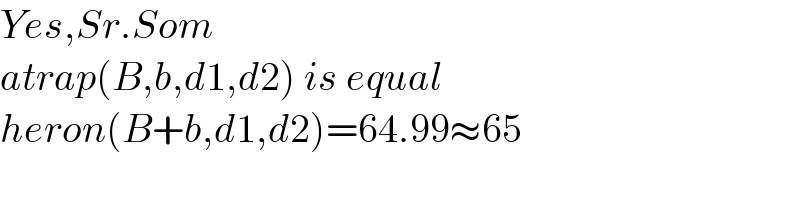
$${Yes},{Sr}.{Som} \\ $$$${atrap}\left({B},{b},{d}\mathrm{1},{d}\mathrm{2}\right)\:{is}\:{equal} \\ $$$${heron}\left({B}+{b},{d}\mathrm{1},{d}\mathrm{2}\right)=\mathrm{64}.\mathrm{99}\approx\mathrm{65} \\ $$
