Menu Close

Question-181394

Tinku Tara 0 Comments
Pin




Question Number 181394 by yaojun2t last updated on 24/Nov/22
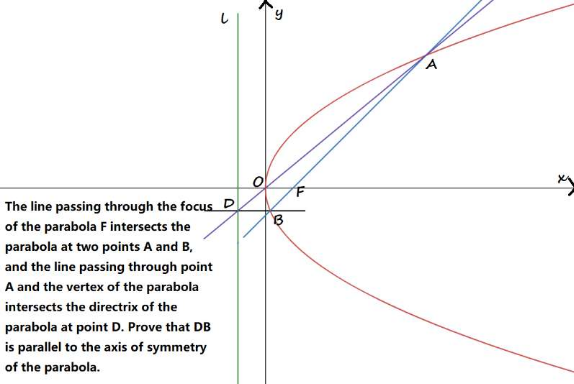
Answered by FelipeLz last updated on 25/Nov/22
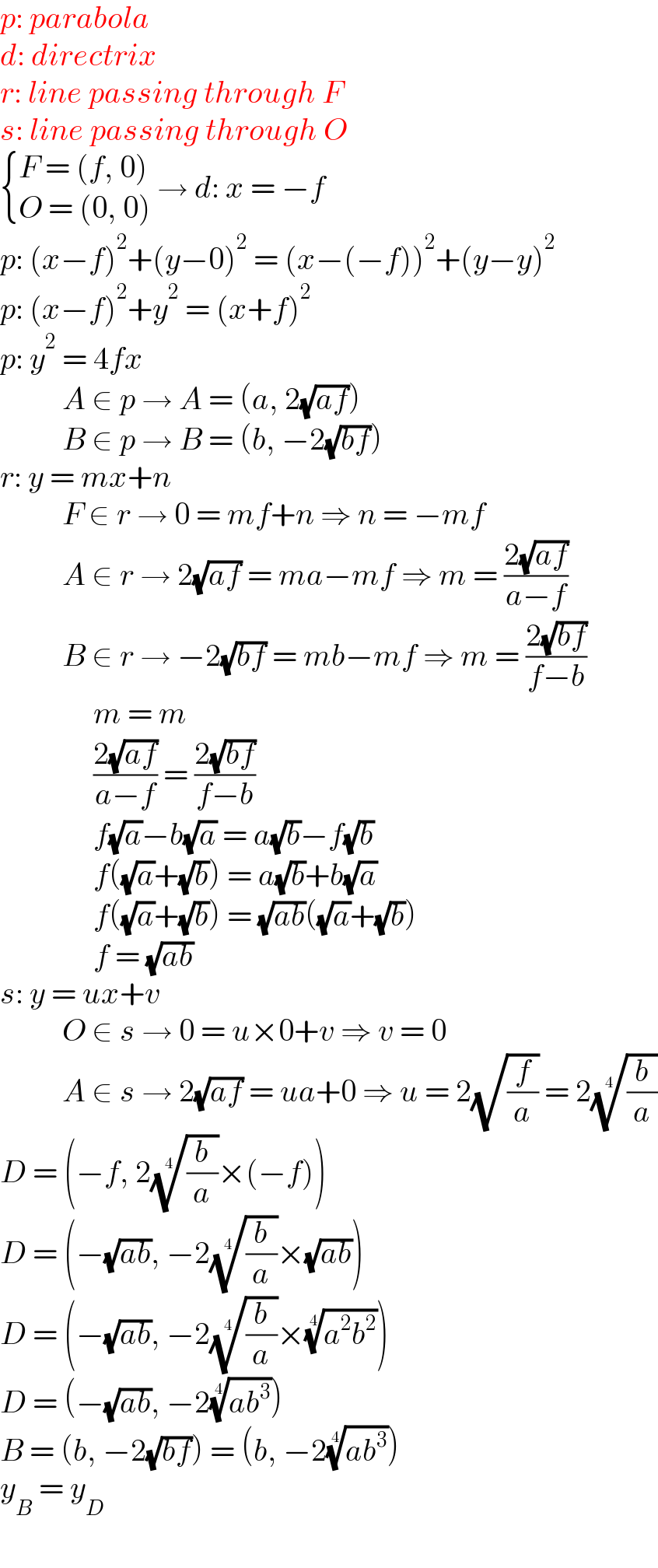
p: parabola d: directrix r: line passing through F s: line passing through O { ((F = (f, 0))),((O = (0, 0) )) :}→ d: x = −f p: (x−f)^2 +(y−0)^2 = (x−(−f))^2 +(y−y)^2 p: (x−f)^2 +y^2 = (x+f)^2 p: y^2 = 4fx A ∈ p → A = (a, 2(√(af))) B ∈ p → B = (b, −2(√(bf))) r: y = mx+n F ∈ r → 0 = mf+n ⇒ n = −mf A ∈ r → 2(√(af)) = ma−mf ⇒ m = ((2(√(af)))/(a−f)) B ∈ r → −2(√(bf)) = mb−mf ⇒ m = ((2(√(bf)))/(f−b)) m = m ((2(√(af)))/(a−f)) = ((2(√(bf)))/(f−b)) f(√a)−b(√a) = a(√b)−f(√b) f((√a)+(√b)) = a(√b)+b(√a) f((√a)+(√b)) = (√(ab))((√a)+(√b)) f = (√(ab)) s: y = ux+v O ∈ s → 0 = u×0+v ⇒ v = 0 A ∈ s → 2(√(af)) = ua+0 ⇒ u = 2(√(f/a)) = 2((b/a))^(1/4) D = (−f, 2((b/a))^(1/4) ×(−f)) D = (−(√(ab)), −2((b/a))^(1/4) ×(√(ab))) D = (−(√(ab)), −2((b/a))^(1/4) ×((a^2 b^2 ))^(1/4) ) D = (−(√(ab)), −2((ab^3 ))^(1/4) ) B = (b, −2(√(bf))) = (b, −2((ab^3 ))^(1/4) ) y_B = y_D
$${p}:\:{parabola} \\ $$$${d}:\:{directrix} \\ $$$${r}:\:{line}\:{passing}\:{through}\:{F} \\ $$$${s}:\:{line}\:{passing}\:{through}\:{O} \\ $$$$\begin{cases}{{F}\:=\:\left({f},\:\mathrm{0}\right)}\\{{O}\:=\:\left(\mathrm{0},\:\mathrm{0}\right)\:}\end{cases}\rightarrow\:{d}:\:{x}\:=\:−{f} \\ $$$${p}:\:\left({x}−{f}\right)^{\mathrm{2}} +\left({y}−\mathrm{0}\right)^{\mathrm{2}} \:=\:\left({x}−\left(−{f}\right)\right)^{\mathrm{2}} +\left({y}−{y}\right)^{\mathrm{2}} \\ $$$${p}:\:\left({x}−{f}\right)^{\mathrm{2}} +{y}^{\mathrm{2}} \:=\:\left({x}+{f}\right)^{\mathrm{2}} \\ $$$${p}:\:{y}^{\mathrm{2}} \:=\:\mathrm{4}{fx} \\ $$$$\:\:\:\:\:\:\:\:\:\:{A}\:\in\:{p}\:\rightarrow\:{A}\:=\:\left({a},\:\mathrm{2}\sqrt{{af}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:{B}\:\in\:{p}\:\rightarrow\:{B}\:=\:\left({b},\:−\mathrm{2}\sqrt{{bf}}\right) \\ $$$${r}:\:{y}\:=\:{mx}+{n} \\ $$$$\:\:\:\:\:\:\:\:\:\:{F}\:\in\:{r}\:\rightarrow\:\mathrm{0}\:=\:{mf}+{n}\:\Rightarrow\:{n}\:=\:−{mf} \\ $$$$\:\:\:\:\:\:\:\:\:\:{A}\:\in\:{r}\:\rightarrow\:\mathrm{2}\sqrt{{af}}\:=\:{ma}−{mf}\:\Rightarrow\:{m}\:=\:\frac{\mathrm{2}\sqrt{{af}}}{{a}−{f}} \\ $$$$\:\:\:\:\:\:\:\:\:\:{B}\:\in\:{r}\:\rightarrow\:−\mathrm{2}\sqrt{{bf}}\:=\:{mb}−{mf}\:\Rightarrow\:{m}\:=\:\frac{\mathrm{2}\sqrt{{bf}}}{{f}−{b}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{m}\:=\:{m} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{2}\sqrt{{af}}}{{a}−{f}}\:=\:\frac{\mathrm{2}\sqrt{{bf}}}{{f}−{b}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\sqrt{{a}}−{b}\sqrt{{a}}\:=\:{a}\sqrt{{b}}−{f}\sqrt{{b}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\left(\sqrt{{a}}+\sqrt{{b}}\right)\:=\:{a}\sqrt{{b}}+{b}\sqrt{{a}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\left(\sqrt{{a}}+\sqrt{{b}}\right)\:=\:\sqrt{{ab}}\left(\sqrt{{a}}+\sqrt{{b}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\:=\:\sqrt{{ab}}\:\:\:\:\:\:\:\: \\ $$$${s}:\:{y}\:=\:{ux}+{v} \\ $$$$\:\:\:\:\:\:\:\:\:\:{O}\:\in\:{s}\:\rightarrow\:\mathrm{0}\:=\:{u}×\mathrm{0}+{v}\:\Rightarrow\:{v}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:{A}\:\in\:{s}\:\rightarrow\:\mathrm{2}\sqrt{{af}}\:=\:{ua}+\mathrm{0}\:\Rightarrow\:{u}\:=\:\mathrm{2}\sqrt{\frac{{f}}{{a}}}\:=\:\mathrm{2}\sqrt[{\mathrm{4}}]{\frac{{b}}{{a}}} \\ $$$${D}\:=\:\left(−{f},\:\mathrm{2}\sqrt[{\mathrm{4}}]{\frac{{b}}{{a}}}×\left(−{f}\right)\right) \\ $$$${D}\:=\:\left(−\sqrt{{ab}},\:−\mathrm{2}\sqrt[{\mathrm{4}}]{\frac{{b}}{{a}}}×\sqrt{{ab}}\right) \\ $$$${D}\:=\:\left(−\sqrt{{ab}},\:−\mathrm{2}\sqrt[{\mathrm{4}}]{\frac{{b}}{{a}}}×\sqrt[{\mathrm{4}}]{{a}^{\mathrm{2}} {b}^{\mathrm{2}} }\right) \\ $$$${D}\:=\:\left(−\sqrt{{ab}},\:−\mathrm{2}\sqrt[{\mathrm{4}}]{{ab}^{\mathrm{3}} }\right) \\ $$$${B}\:=\:\left({b},\:−\mathrm{2}\sqrt{{bf}}\right)\:=\:\left({b},\:−\mathrm{2}\sqrt[{\mathrm{4}}]{{ab}^{\mathrm{3}} }\right) \\ $$$${y}_{{B}} \:=\:{y}_{{D}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *